Московский государственный технический

УНИВЕРСИТЕТ «МАМИ»

Кафедра физики

ЛАБОРАТОРНАЯ РАБОТА 1.06

ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ И МОМЕНТА ИНЕРЦИИ ФИЗИЧЕСКОГО МАЯТНИКА

Москва 2012 г.

Лабораторная работа n 106.

ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ И МОМЕНТА ИНЕРЦИИ ФИЗИЧЕСКОГО МАЯТНИКА

Цель работы: экспериментальное определение ускорения свобод­ного падения и момента инерции физического ма­ятника с использованием оборотного маятника.

Приборы и принадлежности: оборотный маятник, секундомер, масштабная линейка.

ВВЕДЕНИЕ

Физический маятник представляет собой твердое тело, соверша­ющее колебания вокруг неподвижной оси под действием силы тяжести.

Т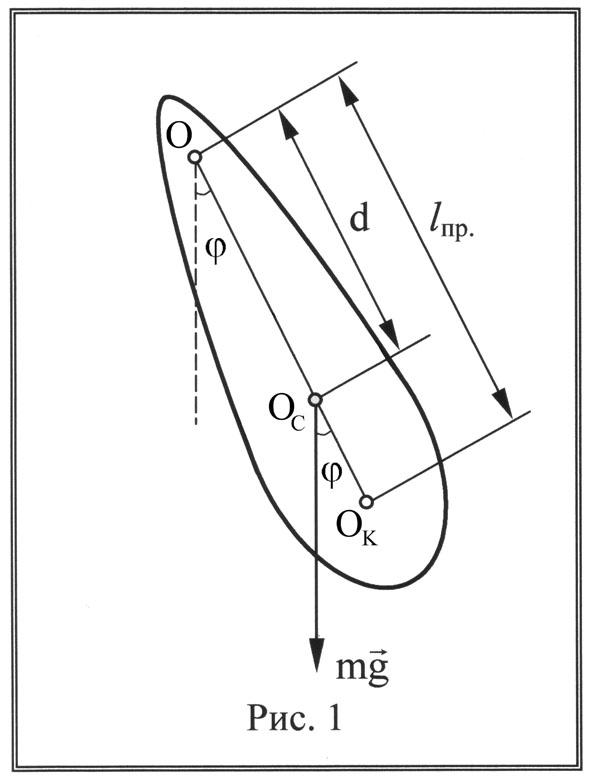акие колебания возможны, если точка подвеса O не совпадает с центром инерции тела С. При отклонении маятника на угол момент силы тяжести стремится вернуть маятник в положение равновесия.

Модуль момента силы тя­жести равен: .

Знак «» обусловлен тем, что вектор направлен в точке O перпендикулярно плоскости ри­сунка «от нас», а вектор уг­лового смещения  «на нас».

На основании основного закона динамики вращательного движения () имеем: , где угловое ускорение . Учитывая, что для малых углов ,

получим .

Разделив полученное уравнение на , и обозначив , получим

(1)

2

Решением этого уравнения является гармоническая функция

, (2)

где  амплитуда колебаний,  циклическая частота колебаний,

 начальная фаза колебаний,

Следовательно, физический маятник, отклоненный на малый угол от положения равновесия, совершает гармонические колебания.

Так как , то для периода колебаний физического маятника получаем следующую формулу: , (3)

где  момент инерции физического маятника относительно оси, проходящей через точку подвеса O, d  расстояние от точки подвеса O до центра инерции С.

Следовательно, период гармонических колебаний физического ма­ятника зависит от момента инерции маятника и ускорения свобод­ного падения g. Обозначим . Величина l_пр называется приведенной длиной физического маятника, под которой понимается длина такого математического маятника, пе­риод колебаний которого равен периоду колебаний данного физического маятни­ка. Тогда период колебаний физического маятника можно записать следующим образом:

, откуда .

Таким образом, для определения ускорения свободного падения нужно определить приведенную длину и период колебаний физического маятника.

Для нахождения приведенной длины физического маятника в дан­ной работе используется так называемый оборотный мятник.

Рассмотрим, что представляет из себя оборотный маятник. Если продолжить прямую ОС и на ней отложить приведенную длину , получим точку К  центр качаний физического маятника (ОК =). Вообще говоря, эта точка может оказаться и за пределами данного физического маятника.

3

Оборотным маятником называется такой физический маятник, центр качаний которого расположен в пределах колеблющегося тела. Центр качаний маятника и точка подвеса обладают свойством взаимозаменяемос­ти. Если маятник перевернуть и подвесить так, чтобы его ось вра­щения проходила через точку К (центр качаний), то прежняя точка подвеса будет совпадать с новым положением центра качаний маят­ника. То есть оборотный маятник можно подвешивать в любой из двух точек О и К без изменения приведенной длины, а следовательно, и периода колебаний.

Если экспериментально определить центр кача­ний, приведенную длину физического маятника можно измерить как расстояние между точкой подвеса оборотного маятника и центром ка­чаний.

ОПИСАНИЕ УСТАНОВКИ.

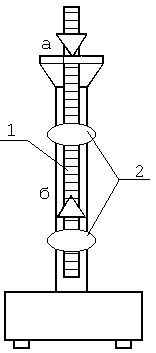
Установка состоит из оборотного маятника 1 (рис. 2), подве­денного на кронштейне, фотоэлектрического датчи­ка и укрепленного на ниж­нем кронштейне секундоме­ра. Оборотный маятник представляет собой метал­лический цилиндрический стержень, на котором зак­реплены два тяжелых груза в виде чечевиц 2 и две опорные призмы а и б. На стержне маятника через 1 см выполнены кольцевые нарезки, служащие для оп­ределения длины.