МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ

УНИВЕРСИТЕТ «МАМИ»

Кафедра физики

ЛАБОРАТОРНАЯ РАБОТА 1.09

ИЗУЧЕНИЕ ПРЕЦЕССИИ ГИРОСКОПА

Москва 2005 г.

Лабораторная работа N 109

ИЗУЧЕНИЕ ПРЕЦЕССИИ ГИРОСКОПА

Цель работы: Определение угловой скорости прецессии и момен­та инерции гироскопа

ВВЕДЕНИЕ

Гироскопом или волчком называется массивное симметричное те­ло. вращающееся с большой скоростью вокруг оси симметрии. На рис.1 изображен гироскоп, вращаю­щийся с угловой скоростью вокруг вертикальной оси симметрии. Угловая скорость и момент импульса гирос­копа направлены вертикально вверх вдоль оси симметрии.

Одно из свойств гироскопа – способность сохранять неизменным направление оси вращения в прост­ранстве при отсутствии момента внешних сил , что следует из за­кона сохранения момента импульса: , если .

Другое свойство гироскопа состоит в том, что при кратковре­менном воздействии на ось гироскопа она сохраняет свое направле­ние в пространстве. Действительно, из основного закона динамики вращательного движения

или

следует, что если момент внешних сил действует в течение корот­кого времени , то изменение момента импульса гироскопа стремится к нулю, и ось гироскопа сохраняет свое нап­равление в пространстве.

Если момент внешних сил, действующих на гироскоп, не равен нулю и не действует кратковременно, ось гироскопа начинает пово­рачиваться в пространстве. Движение оси гироскопа под действием момента внешних сил называется прецессией.

На гироскоп, изображенный на рис. 2, действует момент силы тяжести , где – радиус-вектор, прове­денный из точки О в точку при­ложения силы тяжести . Под действием момента силы тя­жести гироскоп совершает пре­цессию: его ось описывает в пространстве конус. Угловая скорость прецессии равна

(1)

2

где – угол поворота оси гироскопа за время .

Рис 2.

ВЫВОД РАСЧЕТНОЙ ФОРМУЛЫ

У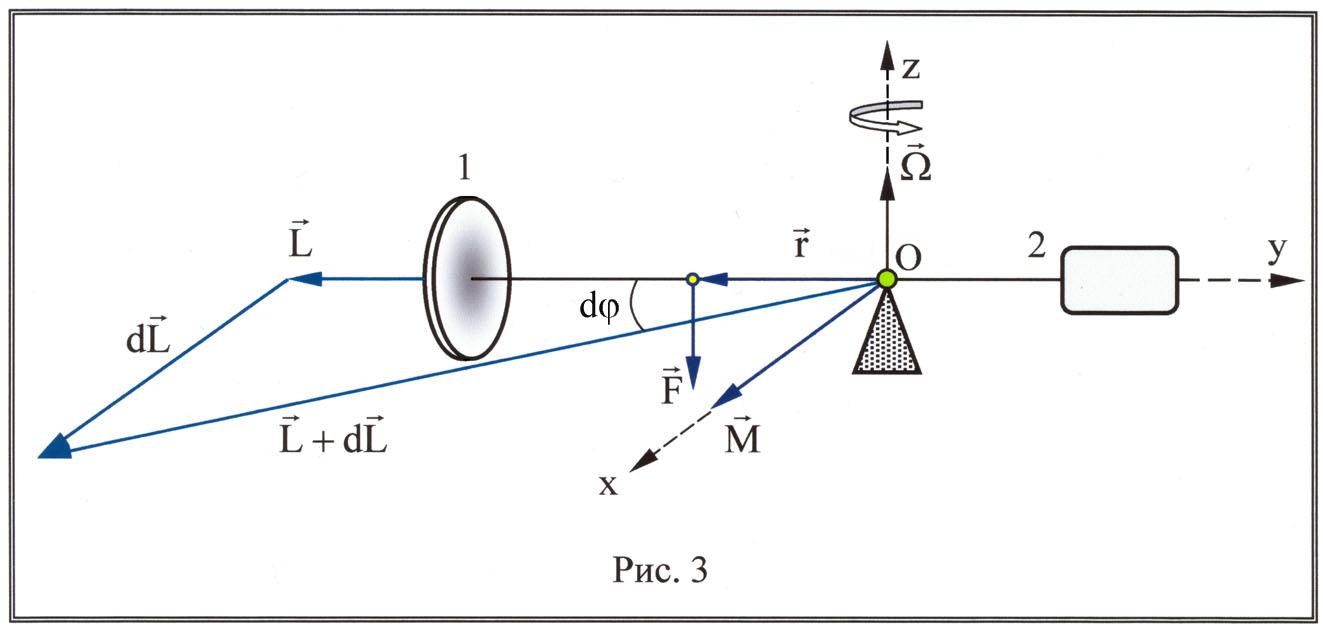прощенная схема гироскопа, используемого в данной лабораторной работе, представлена на рис. 3

Гироскоп имеет одну точку опоры O . Если центр масс системы совпадает с точкой опоры, гироскоп является уравновешенным. Если к оси уравновешенного гироскопа приложена сила , нап­равленная вертикально, вниз, момент этой силы относительно точки О равен , где – радиус–вектор, проведенный из точки О в точку приложения силы.

М

x

омент силы в этом случае направлен вдоль оси х, то есть перпендикулярно силе, и по модулю равен (угол между и равен 90 градусов).

Из основного закона динамики вращательного движения следует, что изменение момента импульса параллельно вектору . Следовательно через момент времени момент импульса гироскопа станет равным , и осъ гироскопа изменит свое положение в пространстве, повернувшись на угол в горизонтальной плос­кости вокруг оси z. При этом момента силы в новом положении снова перпендикулярен оси гироскопа.

Снова произойдет изменение момента импульса и т.д. В результате ось гироскопа под действием момента внешних сил будет непрерывно вращаться в горизонтальной плоскости с некоторой угло­вой скоростью , т.е. будет наблюдаться прецессия.

3

Найдем угловую скорость прецессии . Из рис. 3 видно, что при малых углах поворота оси гироскопа . Следовательно: то есть (2)

В данной работе сила F создается путем смещения груза 2 (рис. 4) из равновесного положения а на расстояние в точку б.

2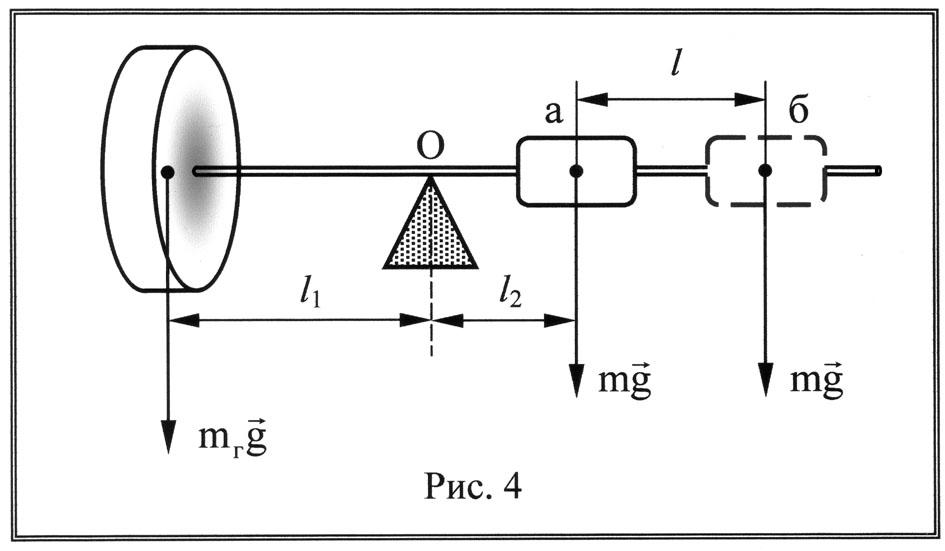

На ось гироскопа действуют моменты силы тяжести гироскопа и груза. В положении равновесия их векторная сумма равна

(3).

где – расстояние от точки О до центра инерции гироскопа. – расстояние от точки О до центра инерции груза. – масса ги­роскопа, m - масса груза.

После смещения груза вправо на расстояние суммарный мо­мент сил относительно точки О будет равен

С учетом (3) имеем (4)

Подставляя момент силы из (4) в формулу (2) получаем формулу для угловой скорости прецессии

, (5)

где m – масса груза, – расстояние, на которое смещают груз, I – момент инерции гироскопа относительно горизонтальной оси симметрии, - угловая скорость вращения гироскопа.

В данной работе экспериментально определяют угловую скорость прецессии по формуле

(6)

4

Определив и пользуясь формулой (5), получим формулу для определения момента инерции гироскопа относительно оси симметрии.

(7)

ОПИСАНИЕ УСТАНОВКИ

О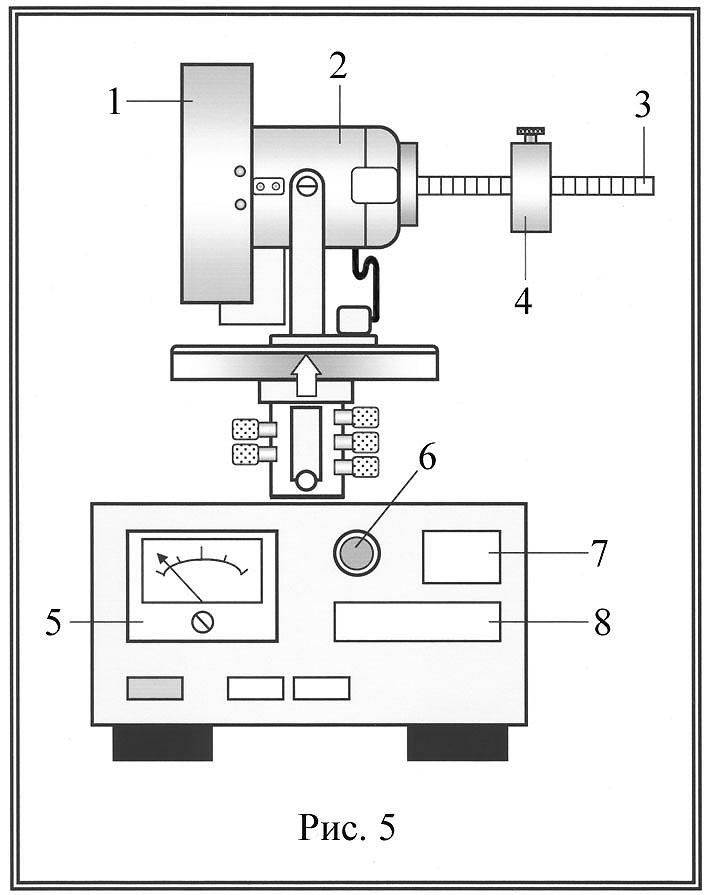бщий вид установки показан на рис. 5.

Массивный маховик 1 (ги­роскоп) может вращаться вокруг горизонтальной оси. Вращение маховика осуществляется электрод­вигателем 2. Скорость вращения маховика может плавно изме-няться от 0 до 6000 об/мин. Рычаг 3, за­крепленный на корпусе двигателя, имеет нанесен­ную метрическую шкалу. На рычаге расположен груз 4, при помощи которого можно уравновесить гироскоп.

На лицевой панели прибора находится: указатель скорости вра­щения электродвигателя 5, регулятор скорости вращения электродви­гателя 6. цифровое табло угла поворота 7 и времени вращения 8.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Нажать клавишу «сеть».

2. При помощи перемещаемого груза установить рычаг гироскопа горизонтально (уравновесить гироскоп).

3. Ручкой «регулятор скорости» включить питание электродви­гателя. Отрегулировать обороты двигателя примерно на 4000 об/мин и поддерживать ее постоянной во время эксперимента. Записать чис­ло оборотов n в таблицу.

4. Переместить груз примерно на 4 см влево или вправо. Изме­рить смещение груза - результаты измерений занести в таблицу.

5. Нажать клавишу «сброс».

5

6. Нажать клавишу «стоп» после того как ось гироскопа по­вернется на 50°-100° (на табло 7 высвечиваются цифры 5-10). Зна­чение угла поворота и времени поворота t занести в таблицу 1.

7. Повторить измерения не менее 3 раз. Все экспериментальные результаты занести в таблицу 1.

Таблица 1.

	n		t

ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

1. Вычислить угловую скорость прецессии по формуле

2. Вычислить момент инерции гироскопа по формуле

3. Рассчитать относительные ошибки и по формулам

;

4. Рассчитать абсолютные ошибки и по формулам

,

5. Окончательные результаты записать в виде

6

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что называется гироскопом?

2. Сформулируйте основной закон динамики вращательного дви­жения.

3. Что называется моментом силы и как определяется его нап­равление?

4. Сформулируйте закон сохранения момента импульса.

5. Что называется угловой скоростью и как определяется ее направление?

6. Выведите формулу для угловой скорости прецессии (2).

7. От чего зависит угловая скорость прецессии гироскопа?

ЛИТЕРАТУРА

1. Детлаф А.А., Яворский Б.М. Курс физики. М.: «Высшая школа».1999 г.

2. Трофимова Т.И. Курс физики. М.: «Высшая школа». 2003г.

3. Савельев И.В. Курс общей физики. М.: «Наука».2001 г. Книги 1,4.

4. Сивухин Д.В. Общий курс физики. М.: «Наука».2003. Т.I.