
Материалы по мат. анализу для самостоятельного обучения / Отчет по практике
.docxФедеральное агентство по образованию РФ
Саратовский Государственный Университет им. Н.Г. Чернышевского
Отчет по практике.
Тема: «Кратные интегралы».
Работу выполнила: студентка 521 гр.
механико-математического факультета
Тимофеева Елена
2008 год.
Содержание:
-
Введение.
-
Примеры задач
-
Ответы.
-
Решение.
Введение.
В моей практической работе я привела несколько примеров вычисления кратных интегралов на заданной области. В приведенных мною примерах областью являются: круг прямоугольный параллелепипед и многие другие. Также в некоторых заданиях область задается неравенством. Все задания моей работы я записала в форме тестов. Всего 10 вариантов заданий. Каждый из них аналогичен по своему следующему. В каждом варианте по 6 заданий. Все они на вычисление двойных и тройных кратных интегралов. В некоторых заданиях вычислить интеграл предлагается указанным способом, например, переходя к полярным координатам. После каждого задания указаны 4 варианта ответа, из которых необходимо выбрать верный.
Для проверки решения далее я прилагаю правильные ответы и пример решения каждого из этих заданий.
Вариант 1
-
Вычислить двойной интеграл
 по прямоугольной области D
(
по прямоугольной области D
(
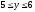 ).
).
а)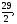 б)
б)
 в)
в) , г)0.
, г)0.
-
Вычислить двойной интеграл:
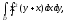 где область D
ограничена кривыми
где область D
ограничена кривыми

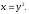
а)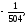 б)
б)
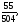 в)
в)
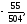 г)
г)
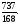
-
Вычислить двойной интеграл, переходя к полярным координатам:
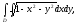 где область D
- круг
где область D
- круг
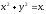
а)
 б)
б)
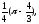 в)
в)
 г)
г)
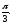
-
Найти площадь, ограниченную кривыми:


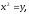

а) б)
б)
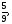 в)
в)
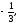 г)
г)

-
Вычислить тройной интеграл:
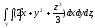 где область V
– прямоугольный параллелепипед (
где область V
– прямоугольный параллелепипед (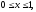
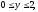
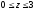 ).
).
а)27,5, б)33,5, в)62, г)26,5.
-
Вычислить тройной интеграл:
 где область V
задается неравенствами
где область V
задается неравенствами



а) 26, б)13, в)7, г)14.
Вариант 2
-
Вычислить двойной интеграл:
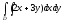 ,
,

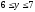 .
.
а)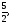 б)
б)
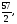 в)
в)
 г)
г)

-
Вычислить двойной интеграл:
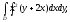

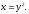
а) б)
б)
 в)
в)
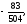 г)
г)
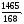
-
Вычислить двойной интеграл, переходя к полярным координатам:


а)
 б)
б)
 в)
в)
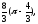 г)
г)
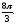
-
Найти площадь, ограниченную кривыми:
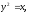
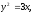
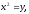
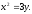
а) б)
б)
 в)
в)
 г)
г)

-
Вычислить тройной интеграл:
 где область V
– прямоугольный параллелепипед (
где область V
– прямоугольный параллелепипед (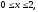
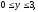
 ).
).
а)296, б)248, в)578, г)216.
-
Вычислить тройной интеграл:
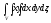 где область V
задается неравенствами
где область V
задается неравенствами

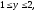
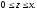
а) 10,5, б)7, в)3,5, г)5,25.
Вариант 3
-
Вычислить двойной интеграл:
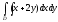 ,
,

 .
.
а)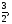 б)
б)
 в)
в)
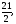 г)0.
г)0.
-
Вычислить двойной интеграл:
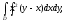

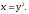
а) б)
б)
 в)
в)
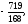 г)
г)

-
Вычислить двойной интеграл, переходя к полярным координатам:


а)
 б)
б)
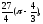 в)
в)
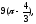 г)
г)

-
Найти площадь, ограниченную кривыми:
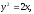

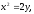

а)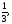 б)
б)
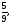 в)
в)
 г)
г)
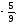
-
Вычислить тройной интеграл:
 где область V
– прямоугольный параллелепипед (
где область V
– прямоугольный параллелепипед (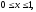

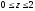 ).
).
а)6, б)7,5, в)4, г)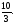
-
Вычислить тройной интеграл:
 где область V
задается неравенствами
где область V
задается неравенствами
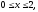
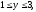
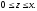
а)
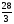 , б)28, в)
, б)28, в) , г)14.
, г)14.
Вариант 4
-
Вычислить двойной интеграл:
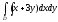 ,
,
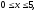
 .
.
а)0, б)20, в)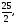 г)80.
г)80.
-
Вычислить двойной интеграл:
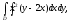

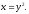
а)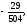 б)
б)
 в)
в)
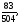 г)
г)
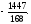
-
Вычислить двойной интеграл, переходя к полярным координатам:
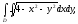
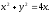
а)
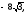 б)
б)
 в)
в)
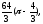 г)
г)
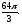
-
Найти площадь, ограниченную кривыми:

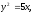

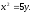
а)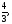 б)
б)
 в)
в)
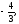 г)
г)
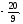
-
Вычислить тройной интеграл:
 где область V
– прямоугольный параллелепипед (
где область V
– прямоугольный параллелепипед (

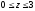 ).
).
а)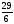 , б)
, б) , в)
, в)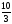 , г)
, г) .
.
-
Вычислить тройной интеграл:
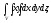 где область V
задается неравенствами
где область V
задается неравенствами

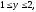
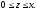
а) 12, б)8, в)6, г)4.
Вариант 5
-
Вычислить двойной интеграл:
 ,
,

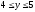 .
.
а) б)
б)
 в)0, г)
в)0, г)
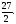
-
Вычислить двойной интеграл:
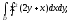


а)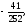 б)
б)
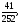 в)
в)
 г)
г)
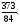
-
Вычислить двойной интеграл, переходя к полярным координатам:
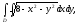
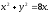
а)
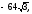 б)
б)
 в)
в)
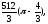 г)
г)
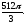
-
Найти площадь, ограниченную кривыми:
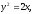


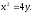
а)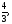 б)
б)
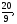 в)
в)
 г)
г)

-
Вычислить тройной интеграл:
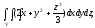 где область V
– прямоугольный параллелепипед (
где область V
– прямоугольный параллелепипед (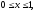

 ).
).
а)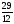 , б)
, б)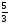 , в)
, в) , г)
, г)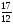 .
.
-
Вычислить тройной интеграл:
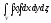 где область V
задается неравенствами
где область V
задается неравенствами
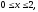
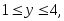

а)
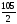 , б)
, б)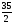 , в)35, г)
, в)35, г)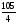 .
.
Вариант 6
-
Вычислить двойной интеграл:
 ,
,
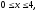
 .
.
а)56, б)176, в)0, г)32.
-
Вычислить двойной интеграл:
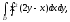
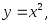
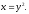
а)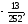 б)
б)
 в)
в)
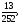 г)
г)
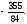
-
Вычислить двойной интеграл, переходя к полярным координатам:


а)
 б)
б)
 в)
в)
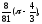 г)
г)
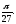
-
Найти площадь, ограниченную кривыми:
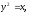
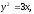
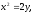
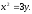
а)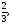 б)
б)
 в)
в)
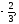 г)
г)
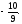
-
Вычислить тройной интеграл:
 где область V
– прямоугольный параллелепипед (
где область V
– прямоугольный параллелепипед (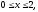

 ).
).
а)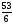 , б)
, б)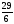 , в)
, в) , г)
, г) .
.
-
Вычислить тройной интеграл:
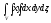 где область V
задается неравенствами
где область V
задается неравенствами
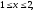
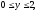

а)
 , б)14, в)
, б)14, в)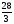 , г)7.
, г)7.
Вариант 7
-
Вычислить двойной интеграл:
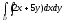 ,
,
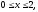
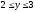 .
.
а)9, б)0, в)29, г)0.
-
Вычислить двойной интеграл:


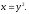
а) б)
б)
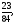 в)
в)
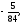 г)
г)
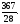
-
Вычислить двойной интеграл, переходя к полярным координатам:
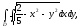
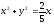
а)
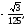 б)
б)
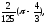 в)
в)
 г)
г)
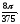
-
Найти площадь, ограниченную кривыми:
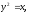



а)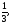 б)
б)
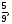 в)
в)
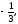 г)
г)
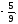
-
Вычислить тройной интеграл:
 где область V
– прямоугольный параллелепипед (
где область V
– прямоугольный параллелепипед (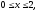
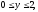
 ).
).
а)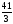 , б)
, б) , в)
, в)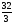 , г)19.
, г)19.
-
Вычислить тройной интеграл:
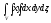 где область V
задается неравенствами
где область V
задается неравенствами
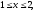


а)
 , б)21, в)
, б)21, в) , г)
, г) .
.
Вариант 8
-
Вычислить двойной интеграл:
 ,
,
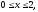
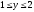 .
.
а)0, б)11, в)3, г)25.
-
Вычислить двойной интеграл:



а)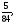 б)
б)
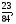 в)
в)
 г)
г)

-
Вычислить двойной интеграл, переходя к полярным координатам:

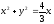
а)
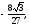 б)
б)
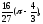 в)
в)
 г)
г)

-
Найти площадь, ограниченную кривыми:
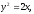

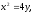

а)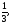 б)
б)
 в)
в)
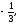 г)
г)
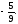
-
Вычислить тройной интеграл:
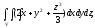 где область V
– прямоугольный параллелепипед (
где область V
– прямоугольный параллелепипед (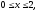

 ).
).
а)48, б)24, в)32, г)40.
-
Вычислить тройной интеграл:
 где область V
задается неравенствами
где область V
задается неравенствами
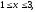


а) 117, б)78, в)58,5, г)39.
Вариант 9
-
Вычислить двойной интеграл:
 ,
,

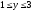 .
.
а)39, б)12, в)0, г)33.
-
Вычислить двойной интеграл:
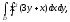
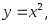

а)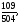 б)
б)
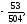 в)
в)
 г)
г)

-
Вычислить двойной интеграл, переходя к полярным координатам:
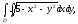

а)
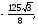 б)
б)
 в)
в)
 г)
г)
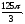
-
Найти площадь, ограниченную кривыми:
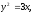

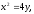
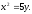
а)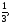 б)
б)
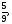 в)
в)
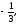 г)
г)
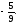
-
Вычислить тройной интеграл:
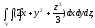 где область V
– прямоугольный параллелепипед (
где область V
– прямоугольный параллелепипед (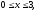
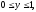
 ).
).
а)42, б)34,5, в)22, г)24.
-
Вычислить тройной интеграл:
 где область V
задается неравенствами
где область V
задается неравенствами

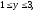
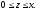
а)
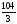 , б)104, в)
, б)104, в)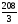 , г)52.
, г)52.
Вариант 10
-
Вычислить двойной интеграл:
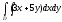 ,
,
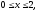
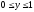 .
.
а)10, б)11, в)0, г)1.
-
Вычислить двойной интеграл:
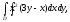


а)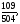 б)
б)
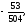 в)
в)
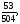 г)
г)

-
Вычислить двойной интеграл, переходя к полярным координатам:


а)
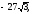 б)
б)
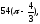 в)
в)
 г)
г)
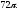
-
Найти площадь, ограниченную кривыми:
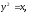

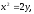

а)-4, б)
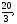 в)
4, г)
в)
4, г)
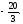
-
Вычислить тройной интеграл:
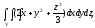 где область V
– прямоугольный параллелепипед (
где область V
– прямоугольный параллелепипед (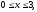
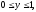
 ).
).
а)10,25, б)19,25, в)13, г)11.
-
Вычислить тройной интеграл:
 где область V
задается неравенствами
где область V
задается неравенствами

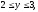
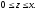
а)
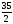 , б)
, б) , в)
, в)
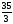 , г)
, г)
 .
.
Ответы:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
а |
б |
в |
а |
а |
б |
|
2 |
б |
а |
в |
а |
б |
в |
|
3 |
в |
а |
в |
а |
в |
а |
|
4 |
г |
а |
в |
а |
а |
г |
|
5 |
а |
б |
в |
а |
г |
б |
|
6 |
б |
в |
в |
а |
б |
а |
|
7 |
в |
б |
в |
а |
а |
в |
|
8 |
г |
в |
в |
а |
в |
г |
|
9 |
а |
а |
в |
а |
г |
а |
|
10 |
б |
в |
в |
в |
а |
б |
