3. Отображение и функции

1) Определение. Соответствие, при котором каждому из элементов множества X сопоставляется единственный элемент из множества Y, называется отображением.

3) Если элементу x соответствует y, то y называется образом элемента x, а x -прообразом элемента y. Пишут: или y = f(x). Множество A всех элементов , имеющих один и тот же образ , называется полным прообразом элемента y.

4) Область определения функции — это все значения x, при которых существует функция.Другими словами, область определения функции, заданной формулой, является все значения аргумента, за исключением тех, которые приводят к действиям, которые мы не можем выполнить. На данный момент мы знаем только два таких действия. Мы не можем делить на нуль и не можем извлечь квадратный корень из отрицательного числа.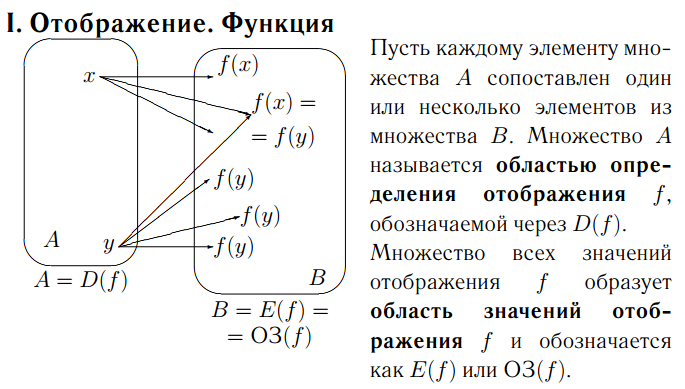

5)Способы задания, виды и св-ва отображений

Способы задания

ВЫРАЖЕНИЕ или ФОРМУЛА. Переменная, вместо которой надо подставлять элемент из области определения, называется аргументом функции. При этом явно указывается процедура вычисления значения f(x) функции f на аргументе x, точнее, при любом значении аргумента. Фактически этим способом мы указываем правило вычисления значения функции f при произвольном значении аргумента x.ТАБЛИЦА. Таблица значений функции состоит, как правило, из двух строк. В первой строке перечисляются все (!) элементы области определения, а во второй строке — соответствующие им значения функции.

ГРАФИК.Графиком функции f называется множество точек плоскости с координатами x, f(x) .

АЛГОРИТМ.X→|A|→y=y(x)

6)Операции над отображениями

1. Обращение y:A→B Y(x)=y

2.Композиция отображений

Y1:A→B y2:B→c

Композиция y1*y2 отображение y1:a->c,такая что y(x)=y1*y2(x)=Z(ЕyϵB)(y1=y1(x)&y2(y)=Z)

7)Ф-ии как спец класс отображений

8)Классификация ф-ий по типу мн-в

3.Бинарные отношения

1)Отношение

2) Бинарным отношениемназывается двухместное отношение между любыми двумя множествамиA и B, т.е. всякое подмножество декартова произведения этих множеств:  A B .

3)примеры Примеры бинарных отношений:

• на множестве целых чисел отношения «делится», «делит», «равно», «больше», «меньше», «взаимно просты»;

• на множестве прямых пространства отношения «параллельны», «взаимно перпендикулярны», «скрещиваются», «пересекаются», «совпадают»;

• на множестве окружностей плоскости «пересекаются», «касаются», «концентричны».

4)Способы задания

5) св-ва бинарных отношений

6) Проекция элемента (a, b) множества Ах В на множество А есть элемент а. Аналогично, элемент b является проекцией элемента (a, b) множества Ах В на множество В. Проекцией множества ЕАх В на А называется множество всех тех элементов из А, которые являются проекциями элементов из Е на множество А

7) Срез бинарного отношения. Различают срез бинарного отношения через элемент и через подмножество первого базисного множества.

8)Факториалы

9)Отношение эквивалентности

10) связь с разбиениями

11) Бинарное отношение ť на мн-ве A(ť AxA) наз-ся отношением толерантности, если оно рефлексивно и симметрично.

12) его связь с покрытием

13) отношение порядка

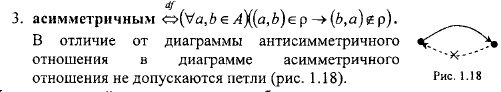
14) стр-ра упорядоченных мн-в

15) Решётка — частично упорядоченное множество, в котором каждое двухэлементное подмножество имеет как точную верхнюю (sup), так и точную нижнюю (inf) грани. Отсюда вытекает существование этих граней для любых непустых конечных подмножеств.Решётка может быть также определена как универсальная алгебра с двумя бинарными операциями (они обозначаются \/и /\ или + и ∙)