Производственная функция “продукт/капитал” и ее свойства
Производственная функция продукт/капитал имеет вид:
,
где Q - объем продукции,
k - капитальный коэффициент,
К - объем капитала
Данная функция используется в планировании капитальных вложений, хотя ей присущи существенные недостатки. Эта функция игнорирует несовершенства рынка, изменения в структуре основного и оборотного капитала, сменности работы оборудования, факторы профессиональной подготовки.
Капитальный коэффициент (k = К/Q),может иметь различные виды: 1) как отношение К/Q при условии неизменности прочих параметров; 2) как историческое отношение К/Q; 3) как проектируемое отношение К/Q, 4) как чистое отношение капитал/продукт, когда из расчетов исключается амортизация; 5) как валовое отношение капитал/продукт; 6) отношение капитал/продукт на основе предположения, что прочие параметры автоматически адаптируются к изменениям; 7) отношение капитал/продукт за единицу времени, когда в расчет принимаются новые вложения.
Домар использовал производственную функцию капитал/продукт для обоснования возможности непрерывного экономического роста, потому что эта функция позволяет выявить величину инвестиций, необходимых для обеспечения требуемого экономического роста. Ход рассуждения таков.
Пусть в экономике часть продукта не потребляется, а сберегается, а из сбережений формируются инвестиции, направляемые на расширение производства. Обозначим
,
где k - отношение капитал/продукция, взятое в применении к приростным величинам;
-
прирост продукции;
I - инвестиции.
Обозначим 
,
где g - темп роста продукции;
-
прирост продукции;
Q - весь объем продукции в течение года.
Тогда 
то есть рост будет обеспечен инвестициями, умноженными на обратную величину капитального коэффициента капитал/продукт.
Если принять инвестиции равными сбережениям, а отношение капитал/продукция постоянным, то
,
где S- сбережения.
Обозначим 
где s- норма сбережений;
S - сбережения;
Q- объем продукции.
В этом случае
g= s/k
То есть темп роста продукции равен норме сбережений, деленной на капитальный коэффициент.
То же самое выводится иным образом:
или g = s/k
Этот результат можно пояснить при помощи числового примера. Предположим, что норма сбережений равна S = 0,2 и что каждый дополнительный прирост капитала на одну единицу вызывает прирост продукции экономической системы на k=0,33. Тогда данная система при прочих равных условиях будет расти с темпом 0, 2 х 0, 33 = 0,066.
Более подробно о производственной функции продукт/капитал см. сн. (1)1.
Производственная функция Кобба-Дугласа и ее свойства
Производственная функция Кобба-Дугласа связывает выпуск Q с величиной капитала К и затратами труда L в виде произведения степеней:
Q
= gK
×
L
Расчет параметров этой производственной функции на основе статистических данных за период 1899-1922 гг. по обрабатывающей промышленности США дал следующие результаты:
Q = 1.01 К 0,27 × L 0,75 ,
где 1.01 - пропорция капитала и труда;
0,27 - доля капитала в созданном продукте,
0,75 - доля труда в созданном продукте.
Модификацией производственной функции Кобба-Дугласа является динамическая производственная функция следующего вида:
Q
= gK
×
L
×
e
где Q - объем продукции;
g - постоянный коэффициент;
К - объем капитала;
L - объем труда;
e
-
основание натурального логарифма;
v- константа;
t- момент времени.
a, b - константы такие, что a + b =1
Логарифмируя, получаем удобное для расчетов линейное уравнение: lg Q = lgg + a lgK + b lg L + evt .
На основе статистики CCCР за 1951-1963 гг. выведены следующие параметры этой производственной функции в логарифмической форме.
lg Q = -0,524 + 1,11 (0,334 lgK + 0,541 lgL + 0,125 lgR + 0, 00518),
где Q - произведенный национальный доход;
К - стоимость капитальных благ;
L - число отработанных человеко-часов;
R - оценка сельскохозяйственных земель,
Геометрическое представление производственной функции Кобба-Дугласа заключается в гиперповерхности в трехмерном пространстве
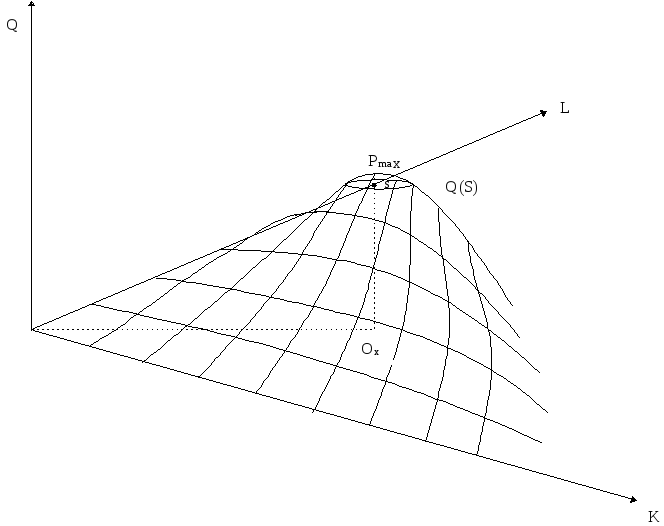
График 22. Геометрическое представление
производственной функции Кобба-Дугласа
Как показано на графике 22 производственная функция Кобба-Дугласа представляет собой гиперповерхность (производственный холм, где точка Qx - представляет собой оптимальное значение продукции и соответствующих ресурсов капитала и труда)2.
Барр Р. выделяет следующие особенности функции Кобба-Дугласа.
1) Если производственные факторы оплачиваются в соответствии с их предельной производительностью, то показатели степени и величин, характеризующих эти факторы, равны соответственно их доле в общем объеме производства.
Рассмотрим это на примере труда.
Предельная производительность труда, полученная путем дифференцирования производственной функции, составляет:
Поскольку предполагается, что заработная плата соразмерна предельной производительности труда, общая масса зарплаты составляет:
Отсюда вытекает:
Такой анализ может быть сделан и в отношении капитала.
2). Поскольку производственная функция содержит шкалу постоянной производительности, сумма величин предельной производительности равна общему объему продукции.
3) Функция Кобба-Дугласа характеризуется тем, что эластичность замещения между трудом и капиталом равна единице. Напомним, что эластичность замещения определяется по формуле:
Если производственную функцию нанести на график с логарифмическим масштабом на обеих осях координат, то коэффициент эластичности покажет наклон этой кривой в соответствующей точке3.