
- •8. Производственные функции
- •Технология производства, понятие производственных функций
- •Производственная функция “продукт/капитал” и ее свойства
- •Производственная функция Кобба-Дугласа и ее свойства
- •Модель экономической динамики Калдора
- •8.5. Введение в линейное программирование
- •8.6. Производственная функция Кейнса
- •9. Теория распределения
- •9.1. Сущность распределения и виды доходов
- •9.2. Эволюция общей теории распределения
- •9.3. Функциональное распределение и его свойства
- •Индивидуальное распределение, его свойства и методы анализа. Закон распределения Парето
8. Производственные функции
8.1. Технология производства, понятие производственных функций
8.2 Производственная функция “продукт \капитал” и ее свойства
8.3. Производственная функция Кобба - Дугласа и ее свойства
8.4. Модель экономической динамики Калдора
8.5. Введение в линейное программирование
8.6 Производственная функция благосостояния Кейнса
Технология производства, понятие производственных функций
Понятие “производство” в обыденном сознании ассоциируется обычно с процессом изготовления, создания определенных осязаемых, или материальных благ. Однако в экономической науке оно имеет более широкое содержание. Экономисты называют производством любую деятельность по использованию естественных ресурсов, включая ресурсы самого человека, для получения как осязаемых, так и неосязаемых (нематериальных) благ. Между производством хлеба и зрелищ, знаний и правосудия, информации и энергии так много технологических различий, что создать единую теорию производства пока не представляется возможным. Но в силу исторической традиции роль такой общей теории выполняет теория материального производства, понимаемого как процесс превращения (трансформации) производственных ресурсов в выпуск (продукт).
Теория производства изучает прежде всего соотношения между количеством применяемых ресурсов и объемом выпуска.
Каждый производственный процесс характеризуется определенной комбинацией ресурсов, безусловно необходимой для получения единицы продукции при данном уровне знаний. Технология производства описывает способ сочетания ресурсов для производства продукта. Чисто техническая зависимость между количеством применяемых ресурсов и объемом выпускаемой продукции в единицу времени (день, месяц, год) выражается через производственную функцию.
Графически каждый способ производства может быть представлен точкой, координаты которой характеризуют минимально необходимые для производства данного объема выпуска количества ресурсов, а производственная функция - линией равного выпуска, или изоквантой.
Каждая изокванта представляет множество минимально необходимых комбинаций производственных ресурсов или технически эффективных способов производства определенного объема продукции. Чем дальше от начала координат расположена изокванта, тем больший объем выпуска она представляет. Наклон изоквант характеризует предельную норму технического замещения одного ресурса другим.
Изокванты могут иметь различную конфигурацию. Линейная изокванта (график 18) предполагает совершенную замещаемость производственных ресурсов, так что данный выпуск может быть получен с помощью либо только труда, либо только капитала, либо с использованием различных комбинаций того и другого ресурса при постоянной норме их замещения. Изокванта, представленная на графике 19, характерна для случая жесткой дополняемости ресурсов. Известен лишь один метод производства данного продукта: труд и капитал комбинируются в единственно возможном соотношении, предельная норма замещения равна нулю. Такую изокванту называют изоквантой леонтьевского типа по имени американского экономиста русского происхождения В.В.Леонтьева, который положил такой тип изокванты в основу разработанного им метода затраты - выпуск.
На графике 20 показана ломаная изокванта, предполагающая наличие нескольких методов производства. При этом предельная норма технического замещения при движении вдоль такой изокванты сверху вниз направо убывает. Изокванта подобной конфигурации используется в линейном программировании - методе экономического анализа, разработанном нобелевскими лауреатами - Т.Купмансом (1910-1985 гг.) и Л.В.Канторовичем (1912-1986 гг.).
На графике 21 представлены изокванты, предполагающие возможность непрерывной, но не совершенной замещаемости ресурсов в определенных границах, за пределами которых замещение одного фактора другим технически невозможно. Традиционная экономическая теория обычно оперирует гладкими изоквантами, изображенными на графике 21, поскольку их анализ не требует применения сложных математических методов. Кроме того, изокванты такого вида можно рассматривать как некую приближенную аппроксимацию ломаной изокванты. Увеличивая число методов производства и, следовательно, множество точек, мы можем (в пределе) представить ломаную изокванту в виде гладкой кривой.
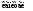

График 18. Линейная изокванта
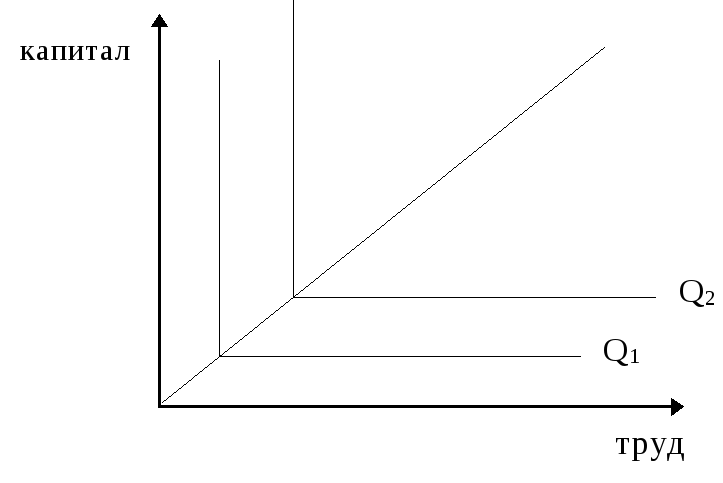
График 19. Изокванта леонтьевского типа

График 20. Ломаная изокванта

Рисунок 21. Гладкие изокванты
В общем виде производственная функция может быть выражена в алгебраических символах
Q = f (a1, a2.....an),
где Q- количество производимой продукции;
а1, а2.....аn - факторы производства
