29. Преломление волн в узловых точках

Рис.8

Переход волны с линии одного сопротивления на линию с другим сопротивлением происходит с преломлением и отражением волн.

К точке А (узловая точка) по линии подходит падающая волна, после точки А по линиидальше будет двигаться уже преломленная волна, а назад пойдет отраженная волна.

откуда

где - коэффициент преломления

Аналогично ,

Где 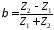- коэффициент отражения

При разомкнутом конце линии (), т.е напряжение на разомкнутом конце линии удваивается.

При коротком замыкании (),.

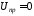При ;,, т.е. волна проходит без преломления.

Для энергия магнитного поля целиком переходит в энергию электрического поля.

Для энергия электрического поля переходит в энергию магнитного поля.

Кроме того, .

 .

Приравняв D к нулю, получим результат, аналогичный (1).

30 Расчет цепей с нелинейными элементами

Нужно найти ВАХ эквивалентного нелинейного элемента

U = U_нэ1 + U_нэ2 по II закону Кирхгофа

Для построения ВАХ эквивалентного нелинейного элемента необходимо произвольным образом взять значения токов и вычислить для этих значений U₁ первого элемента и U₂ второго элемента. Далее, используя II закон Кирхгофа, находим напряжение результирующего элемента для этих значений токов.

В результате получим координаты различных точек результирующей ВАХ.

31. Триггерный эффект в последовательной феррорезонансной цепи

32. Магнитная цепь. Основные законы.

33 Первое уравнение Максвела в дифференциальной форме.

 Первое Максвелла уравнения является обобщением на переменные поля эмпирического Ампера закона о возбуждении магнитного поля электрическими токами. Максвелл высказал гипотезу, что магнитное поле порождается не только токами, текущими в проводниках, но и переменными электрическими полями в диэлектриках или вакууме. Величина, пропорциональная скорости изменения электрического поля во времени, была названа Максвеллом током смещения. Ток смещения возбуждает магнитное поле по тому же закону, что и ток проводимости (позднее это было подтверждено экспериментально). Полный ток, равный сумме тока проводимости и тока смещения, всегда является замкнутым.   Первое Максвелла уравнения имеет вид: ,   (1, a) то есть циркуляция вектора напряжённости магнитного поля вдоль замкнутого контура L (сумма скалярных произведений вектора Н в данной точке контура на бесконечно малый отрезок dl контура) определяется полным током через произвольную поверхность S, ограниченную данным контуром. Здесь j_n — проекция плотности тока проводимости j на нормаль к бесконечно малой площадке ds, являющейся частью поверхности S,  — проекция плотности тока смещения на ту же нормаль, а с = 3×10¹⁰ см/сек — постоянная, равная скорости распространения электромагнитных взаимодействий в вакууме.

34 Второе уравнение Максвела.

 Второе Максвелла уравнения является математической формулировкой закона электромагнитной индукции Фарадея (см. Индукция электромагнитная) записывается в виде: ,   (1, б) то есть циркуляция вектора напряжённости электрического поля вдоль замкнутого контура L (эдс индукции) определяется скоростью изменения потока вектора магнитной индукции через поверхность S, ограниченную данным контуром. Здесь B_n — проекция на нормаль к площадке ds вектора магнитной индукции В; знак минус соответствуетЛенца правилу для направления индукционного тока.