Включение цепи r-l на синусоидальное напряжение
В соответствии со вторым законом Кирхгофа переходной процесс включения описывается уравнением:
где
—
фаза напряжения.
Расчет переходного процесса заключается в определении выражения для тока цепи в функции от времени.
Ток установившегося режима (частное решение):
|
|
где Iт — амплитудное значение тока,
|
|
z — полное сопротивление цепи,
|
|
φ — угол сдвига между напряжением и током,
Свободная составляющая тока определяется как общее
|
|
решение уравнения без свободного члена
Ads by Media WatchAd Options
|
|
|
|
|
— постоянная времени. |
|
|
где А — постоянная интегрирования,
Решение уравнения
|
|
6 Два предельных случая переходного процесса в цепи Rl
7 Разряд конденсатора на активное сопротивление
Если
конденсатор 
,
предварительно заряженный до
напряжения 
замкнуть
в момент 
на
сопротивление 
(рис.1.3),
то будет происходить его разряд. В данном
случае внешнего воздействия нет и
следует рассматривать лишь свободный
процесс в цепи, т.е. уравнение (l.4) будет
,
решением которого является выражение
.
Способы гашения электрической дуги Задачи дугогасительных устройств состоит в обеспечении гашения электрической дуги за минимальное время с допустимым уровнем перенапряжений, малом износе контактов, минимальном объеме распыленных газов, с минимальным звуковым и световым эффектами.
Для
определения константы
интегрирования 
воспользуемся
начальным условием задачи: при 
.Поэтому 
и
тогда решение принимает вид
.
Ток разряда
(1.10)
Сравнивая выражения (1.8) н (1.10),видим, что, как и следовало ожидать, направление тока разряда противоположно направлению тока заряда емкости для этой же цепи. Графики изменения напряжения и тока приведены на рнс.1.4. В процессе разряда емкости вся энергия, запасенная в ней, расходуется в активном сопротивлении в виде тепловых потерь.
8Включение цепи rc под постоянное напряжение
Будем считать, что до коммутации, при t < 0 конденсатор не был заряжен, т.е. существовали нулевые начальные условия: uc = 0, ic = 0.
Рисунок 6.17
t>0 Цепь
описывается уравнением:
,
решение которого uc = ucпр+ucсв.
Поскольку E =
const, то ucпр =
const; 
=0.Конденсатор
не пропускает постоянного тока.
Поэтому ucпр =E, т.е. в установившемся режиме uc уравновесит E и ток в цепи прекратится.
,
где tс = RC.
Объединяем обе составляющие и применяем второй закон коммутации для определения постоянной А.
; uc(0+)
= E + A; uc(-0)
= 0.
uc(0+) = uc(-0), следовательно, E + A = 0, откуда А = -E.
;
(6.33)
Из
полученных выражений можно сделать
вывод, что в первый момент незаряженный
конденсатор равносилен закоротке и 
,
а в установившемся режиме для постоянного
тока конденсатор представляет разрыв
цепи, icпр =
0.
График uc строим по составляющим и складываем их графически. Графики uс и iс представлены на рис. 6.18
9 Включение цепи rc на синусоидальное напряжение
Применим описанную ранее логику для решения задачи включения цепи RC на синусоидальное напряжение (рис. 8.13):
.
Известно, что установившееся значение напряжения на конденсаторе будет синусоидальным:
При 
,
то есть в момент коммутации, 
,если
емкость не была заряжена. Отсюда
.
Значит,
осциллограмма состоит из такой суммы
двух кривых, синусоиды и экспоненты,
что при t = 0 она (сумма) равна нулю (рис.
8.14). Получив такое представление о
процессе и учитывая, что 
,
легко записать решение в виде
.
Теперь
остается только тем или иным способом
определить установившееся значение
напряжения на емкости (
и 
)
по заданным е, R и С:
,
где 
;
.
|
| |
|
|
|
Значит, 
, 
11. Разряд конденсатора на цепь RL
|
Пусть напряжение на конденсаторе в момент коммутации равноU0 , а положительные направления тока и напряжений на элементах цепи такие же как в предыдущем примере(рис. 2.10). В данном случае приложенное напряжение, а также ток установившегося режима ,равны нулю, т.е. e(t)=0 и iПР=0. Тогда из системы уравнений (2.9) получим:
откуда
Окончательно для тока имеем:
и ,соответственно, для напряжений на катушке и на конденсаторе получим:
Последнее
выражение получено с учетом того что Характер процессов при разряде конденсатора зависит от характера корней характеристического уравнения. Исследуем различные возможные случаи. 1) Корни характеристического уравнения вещественны, отрицательны и отличны друг от друга.
Это
имеет место при условии
На
рис. 2.11 изображены кривые i(t), uC(t),
и uL(t).
В интервале времени 0 < t< tmток
по абсолютному значению возрастает
и достигает максимума при
Напряжение
на индуктивности достигает своего
максимума UL max при
t=t2m=2tm, что
находится из условия 2) Корни характеристического уравнения вещественны, отрицательны и равны друг другу.
Данный
случай, когда Получим:
Для напряжений соответственно получим:
Характер
процессов в этом случае не отличается
от рассмотренного выше. Процесс также
апериодический, причем данный случай
является предельным случаем
апериодического разряда, так как при
дальнейшем уменьшении R ниже
значения
3)
Корни характеристического уравнения
комплексные. Это имеет место при Введем обозначения:
Корни характеристического уравнения можем записать в виде
где
угол
Тогда выражение для тока примет вид
С учетом формулы Эйлера
получим
Для uL и uC :
Кривые i, uL и uC представлены на рис 2.12.
Из
полученных выражений и кривых видно,
что процесс в данном случае является
колебательным. Амплитуда колебаний
убывает по показательному закону,
следовательно, в цепи совершаются
затухающие колебания тока и напряжений.
Угловая частота затухающих колебаний
равна
В
предельном случае R=0 и
|
,
.
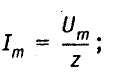
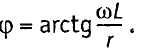
Так как p1<0
и p2<0
и, кроме того, êp2ê>êp1ê,
то при изменении t от 0 до µ разность 
всегда
положительна. Следовательно, ток не
меняет своего направления, т.е.
кондeнсатор
все время разряжается. Такой односторонний
разряд конденсатора называют
апериодическим разрядом.
.
Значение tm находится
из условия 
,
т.е. из условия 
.
В интервале времени tm <
t < µ ток по абсолютному значению
убывает, стремясь к нулю.
.
,
имеет место при 
.
При этом выражения для тока и напряжения
становятся неопределенными из-за
равенства нулю и числителя и знаменателя.
Раскроем эти неопределенности по
правилу Лопиталя, считая что p1-переменная
и стремится к p2.
разряд
становится колебательным.
.
,
лежит
в пределах 
,
так как
и 
.
.Соответственно
период затухающих колебаний определяется
как 
.
Быстроту затухания тока принято
характеризовать так называемым
декрементом колебаний 
равным
отношению двух последующих амплитуд
одного знака:
,а
также логарифмическим декрементом
колебаний, равным 
.
.
В этом случае колебания будут
незатухающими, так как энергия полей
не рассеивается. Угловая частота
незатухающих колебаний 
,
как видим, равна резонансной частоте
контура. Выражения для тока и напряжений
принимают вид