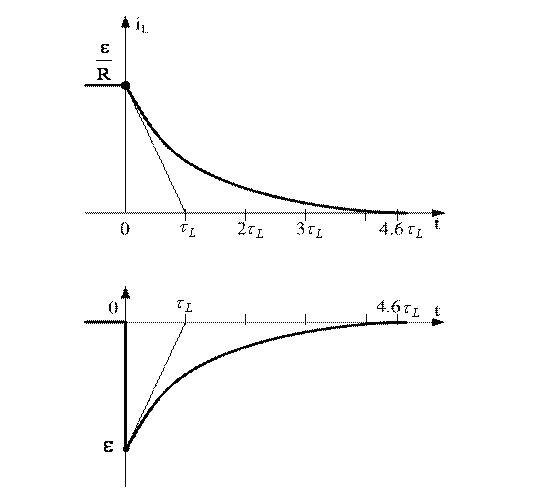3 Переходные процессы в цепи Rl( короткое замыкание)

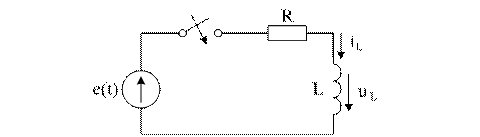
В схеме (рис. 6.3) контакт переключается из положения 1 в положение 2.

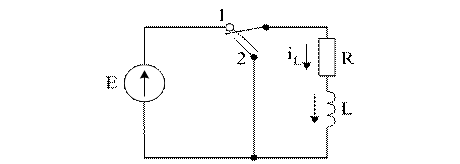
Рисунок 6.3

До коммутации, при t < 0, в цепи под действием постоянной ЭДС, протекал постоянный ток:

.

Напряжение на индуктивности при постоянном токе равно нулю: , т.е. при постоянном токе индуктивность не оказывает сопротивления току, она равносильна закоротке.

После коммутации, при t>0, цепь описывается уравнением: .

В такой цепи i_L пр = 0, поскольку нет стороннего источника. Поэтому

,

где .

Определим постоянную интегрирования А с помощью первого закона коммутации:

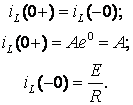
Следовательно, и(6.13). Найдем напряжения на индуктивности:

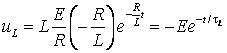. (6.14)

В первый момент после коммутации . Это объясняется тем, что для поддержания тока в цепи на прежнем уровне должна возникнуть ЭДС самоиндукции, а напряжение.

Графики i_L и u_L построены по уравнениям (6.13) и (6.14) и представлены на рис. 6.4.

Физический смысл переходного процесса состоит в том, что за его время энергия, которая была накоплена в магнитном поле до момента коммутации, выделяется в виде тепла в резисторе. Для доказательства вычислим энергию, которая выделяется в виде тепла за время переходного процесса:

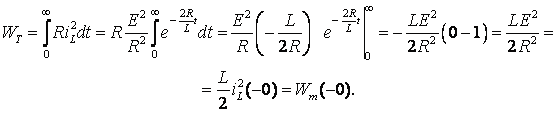
4 Включение rL цепи на постоянное напряжение

Пусть дана цепь (рис.1.1), которая подключается к источнику постоянного напряжения. Параметры цепы заданы: r, L, ключ K работает на замыкание.

Определить ток i (t).

Решение:

В последний момент времени перед замыканием ключа ток в цепи отсутствовал

i(0-) = 0,

где t = 0-.

При t = 0₊ ключ замыкается. Здесь t = 0₊ – первый момент времени после совершения события (замыкания ключа).

Ключ замкнулся, образовался контур. Составим для него уравнение второго закона Кирхгофа:

.

Это уравнение аналогично математическому дифференциальному уравнению первого порядка (ax’ + bx = y).

Решение для тока имеет вид:

,

где –

принужденная составляющая решения, А – постоянная интегрирования, которая может быть найдена из граничных условий.

По характеристическому уравнению: Lp + r = 0

определим корень: .

Обратная величина модуля корня называется постоянной переходного процесса (?):

,

а время переходного процесса равно: t_п.п = (4…5) ?.

В момент времени определим постоянную интегрирования А.

Подставим в решение для тока этот момент:

.

Отсюда А равно:

.

Окончательное решение для тока:

.

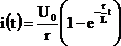Напряжение на индуктивности можно определить по формуле:

.

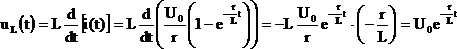Мгновенная мощность источника:

.

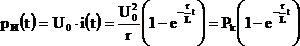Мгновенная мощность нагрузки (r):

.

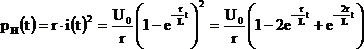Мгновенная мощность нагрузки (L):

.

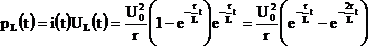Для расчета переходных процессов в цепях классическим методом необходимо знать законы коммутации. В электрических цепях этих законов два.

5 Вкл цепи rl под синусоидальное напряжение.

К схеме (рис. 6.6) при нулевых начальных условиях подключается синусоидальная ЭДС:

.

Рисунок 6.6

При t < 0 i_L = 0, u_L = 0.

При t > 0 . (6.17)

Решение этого уравнения состоит из двух составляющих:

. (6.18)

Поскольку в правой части уравнения (6.17) имеется синусоидальная ЭДС, то после окончания переходного процесса в цепи установится синусоидальный ток:

, (6.19)

где ;.

Для расчета принужденных составляющих i_L пр и u_L пр можно применить также комплексную форму записи. Эта методика будет показана при расчете цепи R, C.

Свободная составляющая не зависит от наличия и вида источника:

; (6.20)

.

Подставляем (6.19) и (6.20) в (6.18) и применим первый закон коммутации для определения постоянной А

. (6.21)

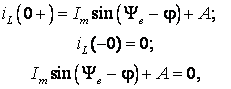
откуда

. (6.22)

Подставив (6.22) в (6.21) получим:

. (6.23)

Напряжение на катушке индуктивности тоже состоит из двух составляющих:, причем, где, а.

.

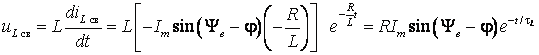Таким образом,

. (6.24)

Поскольку в выражения i_L (6.23) и u_L (6.24) входит величина Y_e, то интенсивность переходного процесса зависит от момента подключения синусоидальной ЭДС. Рассмотрим два крайних случая.

1) Если Y_e = j, то Y_I = 0; 

 – в этом случае не возникает переходный процесс.

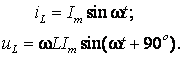
Графики i_L, u_L для этого случая представлены на рис. 6.7.

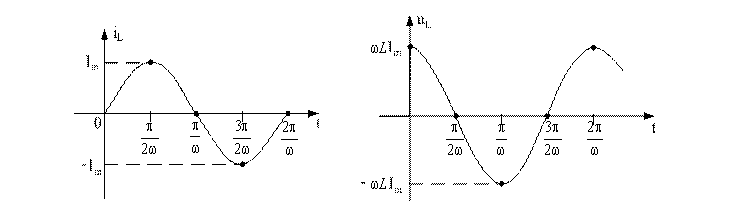
Рисунок 6.7

2) Выберем значение.

;

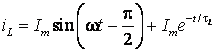 (6.25)

 (6.26)

График тока , построенный согласно (6.25). представлен на рис. 6.8.

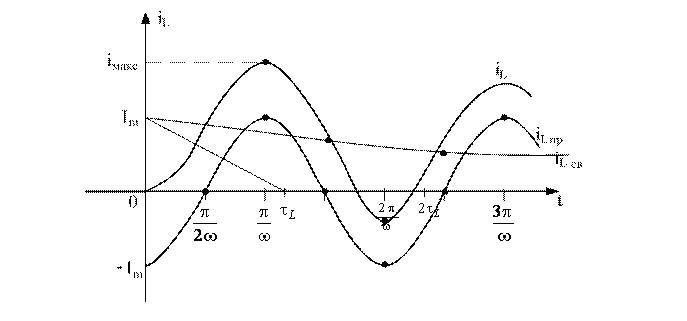
Рисунок 6.8

Если свободная составляющая затухает медленно, что возможно при малом значении R, через полпериода после включения ток достигает наибольшего значения i_макс., которое в пределе стремится к 2I_m, если t®¥. В реальных цепях свободная составляющая всегда затухает, и для выбора электрической аппаратуры принимают i_макс = 1,8 I_m.

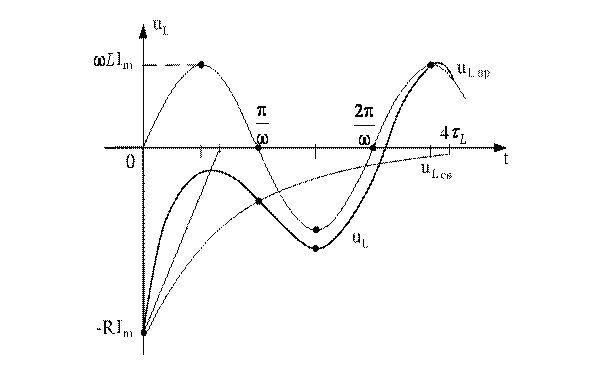
График напряжения u_L показан на рис. 6.9.

Рисунок 6.9

Если R >> wL. то в первый момент после включения возможен значительный скачок напряжения на катушке: . Изоляция электроустановок должна быть выбрана с учетом этого возможного скачка напряжения.

Таким образом, при синусоидальной ЭДС в цепи R, L при определенных условиях возникает сверхток i_макс и перенапряжение на катушке индуктивности.