
- •Математический факультет
- •Введение
- •1.2. Понятие графов и их виды
- •1.3. Способы описания графов
- •1.3.1. Матричное представление графов
- •1.3.2. Теоретико-множественное представление графов
- •1.3.3. Задание графов соответствием
- •Алгоритмы на графах
- •2.1. Алгоритм Беллмана-Форда
- •2.2 Алгоритм Флойда-Уоршелла
- •Заключение
- •Список использованной литературы
1.3.2. Теоретико-множественное представление графов
Граф описывается перечислением множества вершин и дуг. Примеры описания приведены для орграфов на рис.3 и рис.4.
G4 = (Х, А),
где Х = {хi}, i = 1, 2, 3, 4 – множество вершин; А = {ai }, i = 1, 2, ..., 6 – множество дуг, причем А = {(х1, х2), (х4, х2), (х2, х4 ), (х2, х3), (х3, х3), (х4 , х1)}.
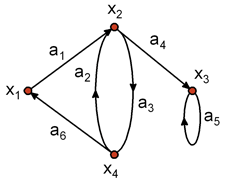
Рис.3. Пример орграфа.
G5 = (X, A),
где X = {B, C, D, E, F} – множество вершин графа, A = {ai}, i = 1, 2, ..., 5 – множество дуг графа, причем a1 = (F, B), a2 = (B, E), a3 = (F, D), a4 = (E, C), a5 = (C, D).
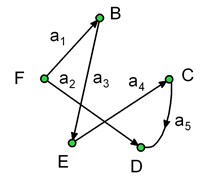
Рис.4. Пример орграфа.
1.3.3. Задание графов соответствием
Описание графов состоит в задании множества вершин Х и соответствия Г, которое показывает, как между собой связаны вершины.
Соответствием Г называется отображение множества Х в Х, а граф в этом случае обозначается парой G = (X, Г).
Отображением вершины хi — Г(хi) является множество вершин, в которые существуют дуги из вершины хi, т. е. Г(хi) = { хj: ∃ дуга (хi, хj) ∈ A}.
Так для орграфа на рис.2 описание заданием множества вершин и соответствия выглядит следующим образом:
G4=(X, Г)),
где X = {хi}, I = 1, 2, ..., 4 – множество вершин, Г(х1) = { х2 }, Г(х2) = { х3, х4 }, Г(х3) = {х3}, Г(х4) = { х1, х2 } – отображения.
Для неориентированного или смешанного графов предполагается, что соответствие Г задает такой эквивалентный ориентированный граф, который получается из исходного графа заменой каждого ориентированного ребра двумя противоположно направленными дугами, соединяющими те же самые вершины. Например, для графа на рис.1,б Г(х2) = { х1, х3, х5 }, Г(х4) ={ х3, х5} и т. д.
Алгоритмы на графах
2.1. Алгоритм Беллмана-Форда
Задан ориентированный взвешенный граф, содержащий, возможно, дуги отрицательного веса. Необходимо найти веса кратчайших путей от вершины v до всех остальных вершин.
Алгоритм решения.
Предположим сначала, что граф не содержит циклов отрицательного веса.
Пусть N –
количество вершин графа, M –
количество дуг, 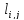 –
вес дуги, ведущей из вершиныi в
вершину j.
Обозначим за
–
вес дуги, ведущей из вершиныi в
вершину j.
Обозначим за 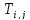 вес кратчайшего пути изv в j,
который содержит не более i дуг.
В случае отсутствия такого пути
положим
вес кратчайшего пути изv в j,
который содержит не более i дуг.
В случае отсутствия такого пути
положим 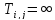 ,
где бесконечность – это некоторое
значение, заведомо превосходящее все
возможные расстояния. При
,
где бесконечность – это некоторое
значение, заведомо превосходящее все
возможные расстояния. При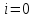 существует единственный допустимый
путь – путь из вершиныv в
неё саму, имеющий нулевой вес.
Соответственно, при
существует единственный допустимый
путь – путь из вершиныv в
неё саму, имеющий нулевой вес.
Соответственно, при 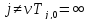 .
Пусть теперь
.
Пусть теперь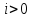 .
Понятно, что кратчайший путь из вершиныv в
вершину j состоит
из кратчайшего пути из v в
некоторую вершину p и
дуги
.
Понятно, что кратчайший путь из вершиныv в
вершину j состоит
из кратчайшего пути из v в
некоторую вершину p и
дуги 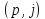 .
Тогда можно записать следующие
рекуррентные соотношения:
.
Тогда можно записать следующие
рекуррентные соотношения:

Здесь V — множество вершин графа, E — множество дуг.
Отметим, что оптимальный путь не должен содержать циклов. В самом деле, если у нас есть некоторый путь с циклом, то, выбросив цикл, мы получим путь меньшего либо равного веса. Тогда максимальное количество дуг в пути будет равно N-1(в противном случае в пути появится цикл).
Если
реализовывать алгоритм непосредственно
по приведённым выше соотношениям, то
его сложность составит O(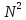 M).
Попробуем
улучшить эту оценку. Заметим, что для
каждой дуги можно однозначно определить,
при решении подзадач для какой именно
вершины она будет использована. Тогда,
вместо того чтобы при каждом i перебирать
все вершины и для каждой из них все
рёбра, можно просто перебрать все рёбра.
Получаем асимптотическую сложность
O(NM).
M).
Попробуем
улучшить эту оценку. Заметим, что для
каждой дуги можно однозначно определить,
при решении подзадач для какой именно
вершины она будет использована. Тогда,
вместо того чтобы при каждом i перебирать
все вершины и для каждой из них все
рёбра, можно просто перебрать все рёбра.
Получаем асимптотическую сложность
O(NM).
Кроме того, нет смысла хранить всю матрицу весов кратчайших путей. Достаточно лишь двух её последних строк. Если же мы немного отойдём от составленных рекуррентных соотношений, то сможем обойтись всего одной строкой. В самом деле, будем брать веса вспомогательных путей из некоторой строки и записывать улучшенные значения в неё же. Тогда после завершения i-ой итерации могут быть найдены веса оптимальных путей, содержащих более чем i дуг, однако все кратчайшие пути, содержащие t дуг, гарантированно будут найдены после выполнения t-ой итерации (действительно, они либо будут найдены на t-ой итерации в соответствии с рекуррентными соотношениями, либо ранее).
Предположим, что нам необходимо вывести также сам кратчайший путь. Тогда для каждой подзадачи необходимо будет сохранять предпоследнюю вершину в пути, т.е. значение k. Это значит, что понадобится матрица размерности NM.
Итак, если все циклы в графе имеют неотрицательный вес, то для нахождения весов кратчайших путей будет достаточно N-1 итерации. Но в противном случае ситуация изменится. Если в пути есть цикл отрицательного веса, то мы можем двигаться по нему бесконечно долго, каждый раз уменьшая длину пути. Произведём тестовую N-ую итерацию. Если после неё изменились какие-то из ранее вычисленных расстояний, то это равносильно тому, что в графе есть цикл отрицательного веса.
Задача 1
Дан взвешенный ориентированный граф из N вершин и M дуг. В графе могут быть как петли, так и дуги отрицательного веса. Требуется найти расстояние от первой вершины до всех остальных. Известно, что в графе нет циклов отрицательного веса и между любой парой вершин не может быть более одной дуги в одном направлении.
Входные данные:
В
первой строке записаны целые числа N
и M –
количество вершин и количество дуг
соответственно
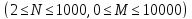 .
Дальше
идет M строк
с тройками целых чисел X, Y, W,
обозначающими, что дуга из X в Y имеет
вес W
.
Дальше
идет M строк
с тройками целых чисел X, Y, W,
обозначающими, что дуга из X в Y имеет
вес W 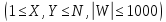 .
.
Выходные данные:
Вывести N-1 строку – длины кратчайших путей от первой вершины до всех остальных вершин в порядке возрастания их номеров. Если же до некоторой вершины не существует пути из первой, то в соответствующей строке необходимо вывести «NO».
import java.io.PrintWriter;
import java.util.Arrays;
import java.util.Scanner;
public class Solution {
private static final int INF = 1000 * 1000 * 1000; //в качестве условной бесконечности выберем достаточно большое число 10^9
public static void main(String[] args) {
Solution solution = new Solution();
solution.solve(); //вызываем процедуру решения задачи
}
private void solve() {
Scanner scanner = new Scanner(System.in);//для считывания воспользуемся классом Scanner
PrintWriter printWriter = new PrintWriter(System.out); //для считывания воспользуемся классом PrintWriter
int vertexCount = scanner.nextInt(); //считываем число вершин графа
int edgeCount = scanner.nextInt(); //считываем число дуг графа
Edge[] edges = new Edge[edgeCount]; //дуги графа будем хранить в массиве
for (int i = 0; i < edgeCount; i++) { //экземпляров класса Edge
int from = scanner.nextInt(); //считываем начальную вершину i-ой дуги
int to = scanner.nextInt(); //считываем конечную вершину i-ой дуги
int weight = scanner.nextInt(); //считываем вес i-ой дуги
from--;
to--; //так как нами используется 0-ая индексация, то уменьшим индексы вершин на единицу
edges[i] = new Edge(from, to, weight); //кладём считанную дугу в массив дуг
}
int[] distance = new int[vertexCount]; //создаем массив, i-ый элемент которого будет хранить текущее расстояние от 1-ой (или 0-ой в нашем случае 0-индексации) до i-ой вершины графа
Arrays.fill(distance, INF); //до начала работы алгоритма все расстояния, кроме 0-го, равны бесконечности (условной)
distance[0] = 0; //0-ое расстояние, очевидно равно нулю, так как расстояние от 0-ой вершины до самой себя равно нулю
for (int i = 0; i < vertexCount - 1; i++) {
for (int j = 0; j < edgeCount; j++) {
int from = edges[j].from;
int to = edges[j].to;
int weight = edges[j].weight; //в соответствии с алгоритмом будем обновлять массив расстояний
if (distance[from] == INF) { //ясно, что если вершина from на текущем шаге работы алгоритма находится бесконечно далеко от 0-ой, то она не изменит ответ
continue;
}
distance[to] = Math.min(distance[to], //В противном случае обновим расстояние до вершины to, это называют релаксацией
distance[from] + weight);
}
}
for (int i = 1; i < vertexCount; i++) {
if (distance[i] == INF) {
printWriter.println("NO");
}
else {
printWriter.println(distance[i]); //выводим расстояние от 0-ой вершины до каждой отличной от нее
}
}
scanner.close(); //закрытие потока ввода
printWriter.close(); //закрытие потока вывода
}
public class Edge {
int from;
int to;
int weight; //для удобства хранения дуг графа создадим класс, содержащий информацию о весе дуги, начальной и конечной вершинах дуги
public Edge(int u, int v, int w) {
this.from = u;
this.to = v;
this.weight = w;
}
}
}
