6. Стационарные и эргодические сигналы. Оценки моментных характеристик для стационарных эргодических сигналов.

Стационарность случайных cигналов подразумевает неизмен­ность их статистических характеристик во времени.

Случайный сигнал называется стационарным в узком смысле, если его - мерные функции закона распределения вероятностей для группы переменных, сдвинутых на время, совпадают и, таким образом, не зависят от времени сдвига

.

Случайный сигнал является стационарным в широком смысле, если его математическое ожидание и дисперсия не зависят от времени- ,, а его корреляционная (ковариаци­он­ная) функция зависит от разности аргументов-,.

Стационарный сигнал является эргодическим, если нахожде­ние его статистических характеристик может быть осуществлено усреднением по одной реализации с помощью интегриро­вания на конечном временном интервале длительностьюс последу­ющим предельным переходом

, ,

, ,

, .

При дискретизации единственной реализа­ции случай­ного стационарного эргодического сигнала ,,-число наблюдений сигнала, возмож­на запись оценокматематического ожидания и дисперсии в следующем виде: ,.

Оценка корреляционной функции представится как функция дискретного аргумен­та ,.

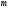7 Дискретное преобразование Фурье для действительного и комплексного случаев.

Дискретное преобразование Фурье для действительного случая

y(i)=y(Ti) – действительные наблюдения.

i=0,1,…,N-1, N – число наблюдений, T – интервал дискретизации. Фиксированные частоты ω_k модели подчиняются соотношениям: .

Модель для полигармонического сигнала примет вид

.

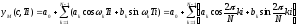Вектор параметров c, так же как и векторная базисная функция φ(Ti) будет иметь размерность (2N-1)

.

Оптимизируемый квадратичный функционал S(c,Y) и соответствующая стандартная задача оптимизации представляется следующим образом:

Введём векторно-матричные обозначения: вектор наблюдений размерности N. матрица плана сигнала размерности (N, (2N-1)) вектор параметров модели размерности (2N-1).

Оптимальные параметры модели с0 вычисляются путём решения системы линейных уравнений

.

Благодаря предложенному расположению частот в модели, базисные функции ортогональны. В этом можно убедиться, если произвести вычисления скалярных произведений для базисных функций, сводящиеся к табличным формулам:

Матрица A=XTX является диагональной, размерностью (2N-1,2N-1), коэффициенты Фурье b=XTY представляют собой взвешенные тригонометрические суммы:

,

Оптимальные коэффициенты модели выразятся через коэффициенты Фурье:

Дискретное преобразование Фурье для комплексного случая

Пусть y(i)=y1(i)+jy2(i) комплексные наблюдения, i=0,1,…,N-1. Комплексная модель для наблюдений имеет вид ,

где - коэффициенты комплексной модели,k=0,1,…,N-1, W – корень N-й степени из единицы:

Функционал S(c,Y) – мера близости комплексных наблюдений и модели, запишется с помощью комплексных сопряжений

Введём векторно-матричные переменные – вектор комплексных наблюдений Y размерности N, комплексную матрицу плана сигнала X размерности (N,N), вектор с комплексных коэффициентов ДПФ размерности N.

Матрица A=X*^TX и вектор коэффициентов Фурье b=X*^TY выразятся с использованием комплексных сопряжений. Коэффициенты ДПФ находятся из системы Ac⁰=b.

Базисные комплексные синусоидальные функции W^ki ортогональны, и поэтому матрица А - диагональная.

Параметры комплексной модели

Вычислим остаточную сумму для оптимальных коэффициентов комплексного ДПФ. Подставим под знак суммы полученные выражения для коэффициентов c(k)

После перемены порядка суммирования убедимся, что имеет место равенство:

Из последнего следует: S(c,Y)=0. Остаточная сумма для данного функционала на оптимальных коэффициентах ДПФ равняется нулю – предлагаемая тригонометрическая модель с нулевой погрешностью аппроксимирует наблюдения. Имеем формулы прямого и обратного ДПФ: