
- •1. Структура системы цос. Структура систем сбора данных
- •2. Аппроксимация наблюдений для линейных моделей, действительный и комплексный случай.
- •3. Модели сигналов на основе действительного и комплексного ряда Фурье Модели сигналов на основе действительного ряда Фурье
- •4. Интеграл Фурье. Свойства Интеграла Фурье
- •Свойства интеграла Фурье.
- •4. Преобразование Фурье для комплексной синусоиды оказывается равным- функции от частоты
- •5 Дискретизация непрерывных сигналов. Теорема Котельникова. Кажущиеся частоты и Противомаскировочная фильтрация.
- •6. Стационарные и эргодические сигналы. Оценки моментных характеристик для стационарных эргодических сигналов.
- •7 Дискретное преобразование Фурье для действительного и комплексного случаев.
- •8. Функции спектральной плотности мощности сигналов. Оценивание функции спм для стационарных эргодических сигналов
- •9. Разностные уравнения цифровых фильтров. Импульсно-переходные функции цифровых фильтров.
- •10. Передаточные функции цифровых фильтров. Передаточные функции на комплексной плоскости
2. Аппроксимация наблюдений для линейных моделей, действительный и комплексный случай.
Аппроксимация наблюдений для линейных моделей (действительный случай)
Рассмотрим случай
линейных дискретных моделей, y(i)=y(Ti),
i=0,1,…,N-1.
Представим модельную функцию сигнала
как
 .
ФункционалS(c,Y),
являющийся мерой близости модели и
наблюдений, определяется разностями
.
ФункционалS(c,Y),
являющийся мерой близости модели и
наблюдений, определяется разностями
 ,представляет
собой квадратичную функцию отс:
,представляет
собой квадратичную функцию отс:
 .
.
Введём векторно-матричные переменные: Y – вектор наблюдений, с – вектор параметров модели, Х – матрица плана сигнала.

 .
.
Функционал
записывается как скалярное произведение
и представляет собой квадратичную форму
 .
Поскольку на переменную с наложены
ограничения, отыскиваемый экстремум
находится путём приравнивания нулю
частных производных введённого
функционала
.
Поскольку на переменную с наложены
ограничения, отыскиваемый экстремум
находится путём приравнивания нулю
частных производных введённого
функционала
 .
.
Приведём
в качестве справки формулы для производных
линейных и квадратичных форм по векторному
аргументу
 .
.
Тогда,
с использованием указанных формул,
учитывая, что
 ,
имеем выражение для оптимального вектора
параметров
,
имеем выражение для оптимального вектора
параметров
 .
.
Матрица
 имеет размерность(m,m);
элементы этой матрицы симметричны
относительно главной диагонали и
определяются как скалярные произведения
базисных функций
имеет размерность(m,m);
элементы этой матрицы симметричны
относительно главной диагонали и
определяются как скалярные произведения
базисных функций
 .
Элементы вектора
.
Элементы вектора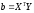 размерностиm
– коэффициенты Фурье вычисляются как
взвешенные суммы наблюдений
размерностиm
– коэффициенты Фурье вычисляются как
взвешенные суммы наблюдений
 .
.
Нахождение с0 оптимального вектора параметров с0 сводится к решению линейной системы уравнений: Ас0=b.
Аппроксимация наблюдений для линейных моделей (комплексный случай)
Введём комплексные наблюдения y(i)=y1(i)+jy2(i) и комплексную модель, задаваемую комплексным вектором параметров и комплексной базисной функцией c(r) = c1(r)+jc2(r), φr(Ti)= φ1r(Ti)+jφ2r(Ti), r=1,…,m, i=0,1,…,N-1,
yM(c,Ti)=cTφ(Ti).
 .
.
Воспользовавшись введёнными векторно-матричными переменными, но в комплексной форме, представим
 .
.
Поделав
соответствующие операции дифференцирования,
но имея ввиду, что переменные –
комплексные, получим выражение для
оптимального комплексного вектора:
 .
.

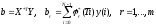 .
.
Если
базисные комплексные функции ортогональны,
то А
будет диагональной с элементами
 .
Оптимальные параметры
модели выразятся через коэффициенты
Фурье
.
Оптимальные параметры
модели выразятся через коэффициенты
Фурье .
.
3. Модели сигналов на основе действительного и комплексного ряда Фурье Модели сигналов на основе действительного ряда Фурье
Пусть
наблюдения cигнала
заданы в виде действительной
функции

![]()
Выбирается модель для указанного сигнала в форме действительного ряда Фурье следующего вида
|
|
|
Значения
модельных частот фиксированы
 ,
, ,
, и определяются длиной интервала
наблюдения, модельные синусоиды
располагаются с шагом по частоте
и определяются длиной интервала
наблюдения, модельные синусоиды
располагаются с шагом по частоте ,
который зависит от
,
который зависит от .
Вектор параметров модели имеет
бесконечную размерность,
.
Вектор параметров модели имеет
бесконечную размерность, ,
, .
Благодаря выбору частотного параметра
.
Благодаря выбору частотного параметра на интервале времени
на интервале времени укладывают целое число периодов
базисных функций
укладывают целое число периодов
базисных функций и
и .Вследствие
этого, указанные базисные функции
являются ортогональными.
.Вследствие
этого, указанные базисные функции
являются ортогональными.
Функционал
для решения задачи аппроксимации
функции
 :
:
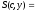
 .
.
Нахождение вектора параметров модели сводится к минимизации указанного функционала
 ,
,
 .
.
Ограничимся
конечным числом синусоид, составляющих
модель,=
 .
В этом случае вектор базисных функций
имеет размерность
.
В этом случае вектор базисных функций
имеет размерность и выглядит на интервале
и выглядит на интервале![]() следующим образом
следующим образом
 .
.
Нетрудно
убедиться в том, что для
![]() составляющие
базис функции ортогональны.
Действительно, легко проверить, что
интегралы от произведений базисных
функций равняются нулю
составляющие
базис функции ортогональны.
Действительно, легко проверить, что
интегралы от произведений базисных
функций равняются нулю
 ,
,
 ,
, ,
,
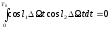 ,
,
 ,
, ,
,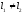 и
и .
.
Вычислим интегралы от квадратов базисных функций
 ,
,
 ,
, .
.
Получим
оптимальные значения коэффициентов
модели для фиксированного


 ,
,
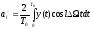 ,
, .
.
Устремим
 .
.
 ,
,
 ,
, .
.
В
силу ортогональности базисных
функций модели ряда Фурье
 ,
, ,
, ,
, .
.
Благодаря
ортогональности данного базиса для
рассматриваемой модели возможно
представление дискретного спектра
мощности в виде бесконечной
последовательности равноотстоящих
на
 по оси частот значений
по оси частот значений .
.
Модели сигналов на основе комплексного ряда Фурье
Пусть
произведено наблюдение комплексной
функции
 на
на![]() ,
модель сигнала представится
комплексным рядом Фурье
,
модель сигнала представится
комплексным рядом Фурье
|
|
|
|
Комплексный
вектор параметров модели имеет
бесконечную размерность

 .
Функционал остаточной суммы примет
вид
.
Функционал остаточной суммы примет
вид
|
|
|
|
пусть
число модельных синусоид = .
вектор базисных функций имеет
размерность
.
вектор базисных функций имеет
размерность
на
интервале времени
![]() составляющие
базис функции ортогональны. Интегралы
от произведений базисных функций
для
составляющие
базис функции ортогональны. Интегралы
от произведений базисных функций
для
 ,
,
 равняются нулю; с учётом комплексности
равняются нулю; с учётом комплексности .
.
Для

 .
.
Оптимальные
параметры модели
 ,
обеспечивающие минимум функционала,
после того как сделаны необходимые
выкладки и предельный переход
,
обеспечивающие минимум функционала,
после того как сделаны необходимые
выкладки и предельный переход ,
определяются следующими интегралами
,
определяются следующими интегралами
|
|
|
|
Пусть
для рассматриваемой функции сигнала
 выполняются условия сходимости с
учётом комплексности. Тогда на
оптимальных
выполняются условия сходимости с
учётом комплексности. Тогда на
оптимальных должно выполняться равенство
должно выполняться равенство
|
|
|
|
Вследствие
(2.5.8) остаточная сумма квадратов
(2.5.6) - значение функционала для
оптимальных параметров должно
принимать нулевое значение
 .
Таким образом
.
Таким образом ,
, ,
, .
.
Для
действительных сигналов
 можно выяснить соотношения между
коэффициентами действительного и
комплексного рядов Фурье
можно выяснить соотношения между
коэффициентами действительного и
комплексного рядов Фурье и
и .
.
 ,
,
 ,
,
 ,
,
 ,
, .
.
Тогда
 ,
, и
и ,
, ,
, .
.
Мощность
 -ой
комплексной модельной синусоидальной
функции вычисляется интегрированием
на интервале
-ой
комплексной модельной синусоидальной
функции вычисляется интегрированием
на интервале![]()
 ,
,
 ,
,
 ,
,
 .
.
Благодаря ортогональности используемого комплексного базиса общая мощность сигнала представляется в виде суммы мощностей составляющих как для положительных, так и отрицательных частот.




 ,
,

 .
.
 .
. ,
,
 .
. .
.