4. Интеграл Фурье. Свойства Интеграла Фурье

Интеграл Фурье реализуется на основе рассмотрения комплексного ряда Фурье для бесконечного временного интервала; будем полагать, что сигнал с конечным числом точек разрывов определён дляи для него выполняется условие абсолютной интегрируемости.

Данные условия являются достаточными для существования преобразования Фурье сигнала .

Без потери общности примем временной интервал симметричным , пусть этот интервал расширяется

, ,.

Запишем коэффициенты разложения комплексного ряда Фурье для расширяющегося временного интервала

, .

Подставим выражение в .

Устремим , обозначим,, получим в пределе

.

Сформируем интегралы ,.

Функцию называют интегралом Фурье или преобразованием Фурье для. Два последних интеграла являются прямым и обратным преобразованием Фурье. Сигнал представляется как во временной области при традиционном анализе, так и в частотной области в виде непрерывных коэффициентов разложений Фурье ,.

Функция в общем случае является комплексной функцией частоты и допускает следующие представления

, ,

где и-действительные и мнимые части,,-модуль и фаза преобразования Фурье.

Свойства интеграла Фурье.

.

1. Из определения преобразования Фурье следует его линейность или свойство суперпозиции. Пусть функция представляет собой взвешенную сумму функций, для которых заданы их преобразования Фурье

, . Тогда,.

2. Пусть масштабирующий множитель преобразующий функцию в, и.

, .

Введём переменную ,

, .

3. Пусть задано преобразование Фурье для функции :.Введём запаздывание (сдвиг по времени) для функции , сформируем. Вычислим преобразование Фурье для

,

.

Сделав аналогичные выкладки, получим, что преобразование Фурье для функции , умноженной на, сдвигается по частоте

, .

4. Преобразование Фурье для комплексной синусоиды оказывается равным- функции от частоты

. Действительно, .

5. Пусть преобразование Фурье для функции. Найдёмвыражение для преобразования Фурье для производной . Запишем выражение для обратного преобразования Фурье и продифференцируем его

, .

Из последнего выражения следует, что

.

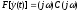Сделав почти аналогичные выкладки, можно записать преобразование Фурье для интеграла от , которое будет иметь вид

.

6. Вычислим преобразование Фурье для симметричного единичного импульса

, ,,,

.

Ввиду симметричности рассматриваемого единичного импульса, его преобразование Фурье является действительной функцией.

7. Найдём преобразование Фурье для произведения функций ,- соответственно преобразования Фурье для. Запишем интегралы

.

Изменив порядок интегрирования, с учётом выражения интеграла Фурье для комплексной синусоиды, получим

.

Преобразование Фурье от произведения функций равняется свёртке преобразований Фурье сомножителей.