8.4.1. Модель авторегрессии 1-го порядка (ар(1))

Рассмотрим модель авторегрессии АР(1): (t)=₁(t-1)+u(t). Здесь M[(t)]=0, cov((t),(t-1))0. При умножении обеих частей уравнения на (t-1) получим соотношение:

(t-1) (t)= (t-1) ₁(t-1)+u(t) (t-1). Математическое ожидание равно автоковариационной функции (1): M[(t-1) (t)]=M[(t-1) ₁(t-1)+u(t) (t-1)].

Отсюда (1)=₁(0). Математическое ожидание от слагаемого u(t)(t-1) равно 0 в силу независимости случайных величин u(t) и (t-1). Таким образом, искомый коэффициент ₁=(1)/(0) = (1).

Условие стационарности процесса состоит в том, что |₁|<1. Линейная зависимость между остатками позволяет определить дисперсию: 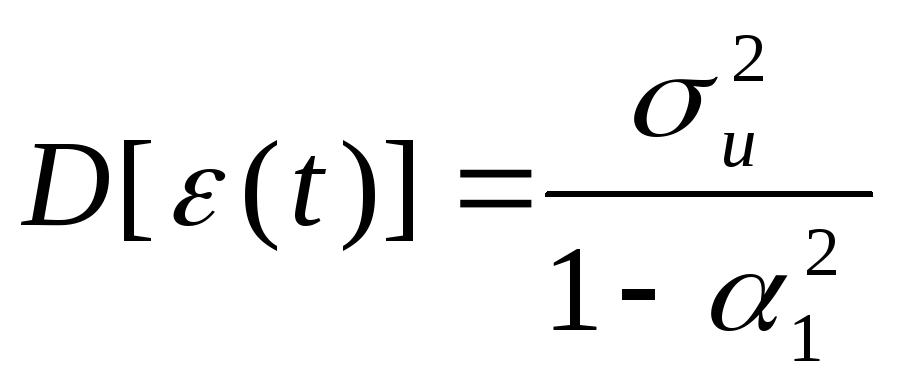, и ковариацию

cov((t),(t-k)) = (доказательство см. [1, с.691]).

8.4.2. Модель авторегрессии второго порядка - ар(2)

Эта модель, как и АР(1), представляет собой частный случай авторегрессионнного преобразования, когда все коэффициенты _i, кроме первых двух, равны нулю. Соответственно, она может быть определена выражением

, где последовательность величин u(t), u(t-1), u(t-2) и т.д. образует белый шум. Умножая обе части уравнения поочередно на (t-1) и (t-2) и беря математические ожидания от двух полученных таким образом соотношений, получаем систему уравнений, связывающую между собой параметры ₁ и ₂ с дисперсией (0)=D[(t)] и первыми двумя ковариациями (1)=M[(t)(t-1)] и (2)=M[(t)(t-2)] анализируемого процесса (t):

,

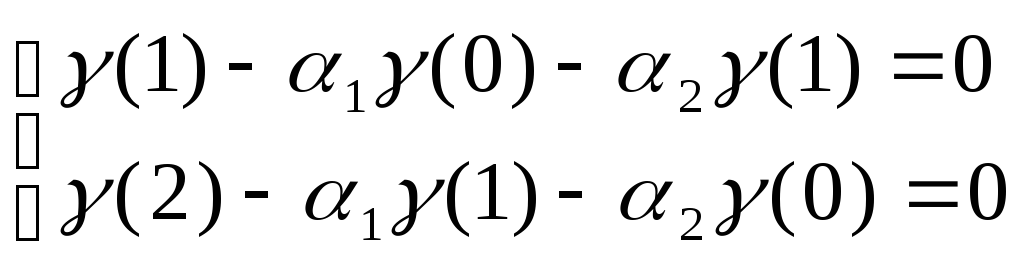или, после деления обоих уравнений на (0):

.

Разрешая эту систему относительно 1 и 2, имеем:

Условиями стационарности ряда (подробно [1, с.830]) являются

8.4.3. Модель авторегрессии ар(s)

Обобщая использованный прием, рассмотрим идентификацию модели АР(s).

Домножим уравнение на (t-), возьмем математическое ожидание и получим:

. Делением на (0) получим соотношение . Подставляя=1,2,…,s получим систему s уравнений, разрешимую относительно s неизвестных ₁, ₂, …_s:

Здесь мы воспользовались свойством автокорреляционной функции (0)=1.

8.4.4. Модель авторегрессии – скользящего среднего арсс(1,1)

В соответствии с определением (п.8.4) процесс АРСС(1,1) описывается формулой

Введем обозначение _u(k)=M[(t-k)u(t)]. Очевидно _u(k)=0, если k>0 в силу независимости(t-k) и u(t), однако, это неверно для k0.

Для идентификации модели домножим уравнение поочередно на (t), (t-1), (t-2) и возьмем математическое ожидание. Получим систему из трех уравнений, которая разрешима относительно трех неизвестных: ,  и _u(-1):

Условиями стационарности временного ряда являются (подробно [1, с.851]):

8.5. Модели нестационарных временных рядов и их идентификация

Удовлетворительные (в прикладном смы­сле) результаты в моделировании случайных остатков можно получить, оставаясь в рамках класса моделей стационарных временных рядов. Од­нако сами реальные временные ряды x(t), встречающиеся в экономике, финансах, торговле, маркетинге, за редкими исключениями являются не­стационарными. Правда, их нестационарность чаще всего проявляется лишь в наличии зависящей от времени t неслучайной составляющей f(t). В подобных случаях говорят о нестационарности на уровне первых мо­ментов, или о нестационарных однородных временных рядах. Иначе го­воря, временной ряд x(t) называется нестационарным однородным, если его случайный остаток (t), получающийся вычитанием из ряда x(t) его неслучайной составляющей f(t), представляет собой стационарный (в ши­роком смысле) временной ряд.