92

Модуль 6. Обобщенный метод наименьших квадратов

В предыдущих разделах были рассмотрены модели парной и множественной линейной регрессии, а также задачи экономического анализа, решаемые с помощью этих моделей. Наиболее распространенным в практике статистического оценивания параметров уравнений регрессии является метод наименьших квадратов. Этот метод основан на ряде предпосылок относительно природы данных и результатов построения модели. Основные из них - это четкое разделение исходных переменных на зависимые и независимые, некоррелированность факторов, входящих в уравнения, линейность связи, отсутствие автокорреляции остатков, равенство их математических ожиданий нулю и постоянная дисперсия. Эмпирические данные не всегда обладают такими характеристиками, т.е. предпосылки МНК нарушаются. Применение этого метода в чистом виде может привести к таким нежелательным результат как смещение оцениваемых параметров, снижение их состоятельности, устойчивости, а в некоторых случаях может и вовсе не дать решения. Для смягчения нежелательных эффектов при построении регрессионных уравнений, повышения адекватности моделей существует ряд усовершенствований МНК, которые применяются для данных нестандартной природы.

6.1. Обобщенный метод наименьших квадратов

Пусть V— некоторая симметричная, положительно определенная матрица порядкапп,гдеп, как и прежде, число исходных статистических данных, т. е. объем имеющейся в нашем распоряжении выборки).

Пусть по прежнему М(_i)=0 гдеi=1…n.предположим, что остатки _i некоррелированы между собой, но имеют разные дисперсии. В этом случае квадратнуюматрицу ковариацийможно представить в виде симметричной положительно определенной матрицы

M[^T] = ²V ( 6.0)

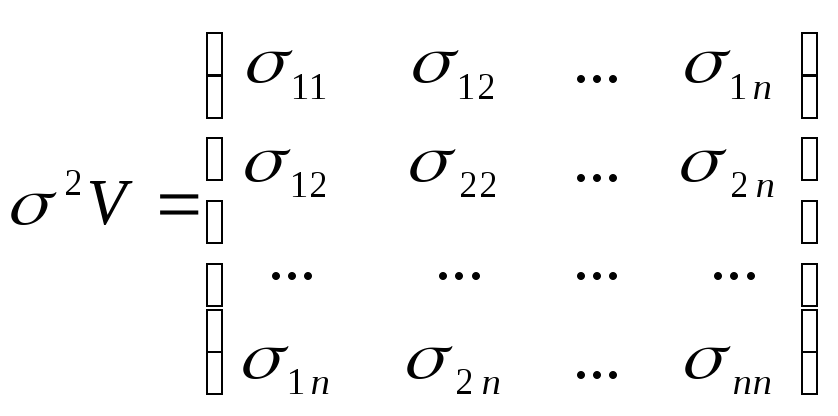
где cov(_i, _j) =_ij при ij; cov(_i,_i)=_ii – дисперсия элемента _i.

Будем предполагать, что в этом соотношении число  неизвестно, а матрица V известна. С точки зрения практической, прикладной последнее предположение в большинстве случаев нереалистично; однако в дальнейшем для некоторых частных случаев мы сможем отказаться от условия априорного знания матрицыV.

Задача заключается в отыскании оценок коэффициентов (см. 4.1.1.) в модели

у = Х+ , ( 6.0)

когда M[^T] =²V.

Положительно определенная матрица допускает представление в виде РР^Т, где матрицаРневырожденная. Поэтому запишемV= РР^Т, так что

Р^-1VР^Т-1 =Е,( 6.0)

где Е– единичная матрица, и

(Р^Т)^-1 Р^-1= V^-1 ( 6.0)

Умножим уравнение модели у = Х+  слева на матрицу Р^-1, получим

у* = Х*+ * ( 6.0)

Где у*= Р^-1у; Х* = Р^-1Х и*= Р^-1 .

Используя (6.3), легко показать, что M[**^T] =²Е,

Т.е. (6.5) удовлетворяет всем предположениям обыкновенной модели наименьших квадратов. В частности (мы воспользуемся равенством (6.4)),

( 0.6)

Есть несмещенная линейная оценка вектора , обладающая наименьшей дисперсией и матрицей ковариаций:D[]=²(Х*^ТХ*)^-1=²(Х^ТV^-1Х)^-1.

Несмещенная оценка для ²может быть выведена как

Далее, если предположить, что удовлетворяет нормальному распределению, то этим же свойством будет обладать и*. Поэтомуобладает минимальной дисперсией в классе несмещенных оценок.

Оценка , определенная с помощью (6.6), представляет собой оценку обобщенного метода наименьших квадратов. Заметим, что если мы применим к модели (6.2) обыкновенный метод наименьших квадратов, то получим оценку, которая будет линейной и несмещенной, ноне будетобладать наименьшей дисперсией. Замена обычного условияM(^T) =²Еусловием (6.1) ведет к нарушению для обыкновенного метода наименьших квадратов свойства наименьшей дисперсии оценок.