
- •Раздел 1. Теория вероятности
- •Глава 1. Основные понятия и теоремы теории вероятностей Параграф 1. Понятие о случайном событии
- •Параграф 2. Действия над событиями
- •Параграф 3. Классическое определение вероятности
- •Параграф 4. Статистическое определение вероятности
- •Параграф 5. Геометрическое определение вероятности
- •Параграф 6. Элементы комбинаторики
- •Параграф 7. Теоремы произведения вероятностей
- •Параграф 8. Теоремы сложения вероятностей
- •Параграф 9. Формула полной вероятности
- •Параграф 10. Формула Байеса
- •Глава 2. Повторные независимые испытания Параграф 1. Формула Бернулли
- •Параграф 2. Формула Пуассона
- •Параграф 3. Локальная теорема Муавра-Лапласа
- •Параграф 4. Интегральная торема Муавра-Лапласа
- •Глава 3. Случайные величины Параграф 1. Понятие случайной величины
- •Параграф 2. Действия над случайными величинами
- •Параграф 3. Дискретная случайная величина
- •Параграф 4. Функция распределения
- •Параграф 5. Непрерывная случайная величина
- •Параграф 6. Мода и медиана. Квантили. Моменты случайных величин. Асимметрия и эксцесс
- •Глава 4. Основные законы распределения Параграф 1. Биномиальный закон распределения
- •Параграф 2. Закон распределения Пуассона
- •Параграф 3. Геометрическое распределение
- •Параграф 4. Гипергеометрическое распределение
- •Параграф 2. Дискретная многомерная случайная величина
- •Параграф 3. Функция распределения многомерной случайной величины
Раздел 1. Теория вероятности
Глава 1. Основные понятия и теоремы теории вероятностей Параграф 1. Понятие о случайном событии
Опыт или наблюдение явления называется испытанием.
Пример 1. Бросание монеты; выстрел из винтовки; бросание игральной кости.
Результат или исход испытания называется событие.
Пример 2. Выпадение герба или выпадение цифры; попадание в цель или промах; появление того или иного числа очков на брошенной игральной кости.
Для
обозначения событий используются
большие буквы латинского алфавита:
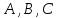 и т.д.
и т.д.
События называются совместимыми, если появление одного из них не исключает появление другого в одном и том же испытании.
Пример
3. Испытание: однократное бросание
игральной кости. Событие
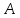 – появление четырех очков; событие
– появление четырех очков; событие – появление четного числа очков. События
– появление четного числа очков. События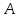 и
и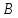 совместимые, так как появление одного
из них не исключает появление другого.
совместимые, так как появление одного
из них не исключает появление другого.
События называются несовместимыми, если появление одного из них исключает появление другого.
Пример
4. Испытание: однократное бросание
монеты. Событие
 – выпадение герба; событие
– выпадение герба; событие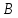 – выпадение цифры. События
– выпадение цифры. События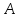 и
и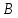 несовместимые, так как появление одного
из них исключает появление другого.
несовместимые, так как появление одного
из них исключает появление другого.
Событие называется достоверным, если в данном испытании оно является единственно возможным его исходом.
Событие называется невозможным, если в данном испытании оно заведомо не может произойти.
Пример
5. Испытание: Извлечение шара из урны, в
котором все шары белые. Событие
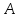 – вынут белый шар – достоверное событие;
событие
– вынут белый шар – достоверное событие;
событие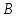 – вынут черный шар – невозможное
событие.
– вынут черный шар – невозможное
событие.
Событие называется случайным, если оно объективно может наступить или не наступить в данном испытании.
Пример
6. Испытание: однократное бросание
игральной кости. Событие
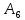 – выпадение шести очков – случайное
событие, так как оно объективно может
наступить или не наступить в данном
испытании.
– выпадение шести очков – случайное
событие, так как оно объективно может
наступить или не наступить в данном
испытании.
События называются противоположными, если в данном испытании они несовместимы и одно из них обязательно происходит.
Событие,
противоположное событию
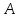 ,
обозначается через
,
обозначается через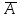 .
.
Пример
7. Испытание: однократное бросание
монеты. Событие
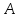 – выпадение герба (не выпадение цифры);
событие
– выпадение герба (не выпадение цифры);
событие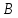 – не выпадение герба (выпадение цифры).
События
– не выпадение герба (выпадение цифры).
События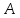 и
и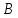 противоположны
противоположны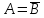 или
или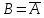 ,
так как они несовместимы и одно из них
обязательно происходит.
,
так как они несовместимы и одно из них
обязательно происходит.
Параграф 2. Действия над событиями
Произведением событий называется событие, состоящее в совместном наступлении всех этих событий.
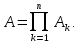
Пример
1. Испытание: два стрелка делают по
выстрелу. Событие
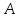 – попадание в цель первым стрелком;
событие
– попадание в цель первым стрелком;
событие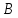 – попадание в цель вторым стрелком.
Событие
– попадание в цель вторым стрелком.
Событие – попадание в цель первым и вторым
стрелком вместе.
– попадание в цель первым и вторым
стрелком вместе.
Суммой событий называется событие, состоящее в наступлении хотя бы одного из данных событий.
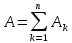
Пример
2. Испытание: два стрелка делают по
выстрелу. Событие
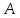 – попадание в цель первым стрелком;
событие
– попадание в цель первым стрелком;
событие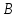 – попадание в цель вторым стрелком.
Событие
– попадание в цель вторым стрелком.
Событие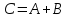 – попадание в цель первым или вторым
стрелком.
– попадание в цель первым или вторым
стрелком.
Разностью событий называется событие, которое состоит в том, что одно из событий не произойдет.
Пример
3. Испытание: два стрелка делают по
выстрелу. Событие
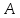 – попадание в цель первым стрелком;
событие
– попадание в цель первым стрелком;
событие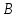 – попадание в цель вторым стрелком.
Событие
– попадание в цель вторым стрелком.
Событие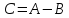 – попадание в цель первым стрелком и
промах второго стрелка.
– попадание в цель первым стрелком и
промах второго стрелка.
Диаграмма Венна и свойства действий над событиями.

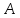
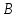



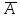
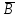
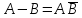
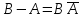

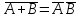
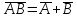


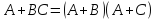
 ;
;
 ;
;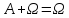 ;
;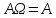 ;
;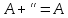 ;
;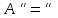 .
.
Рис. 1.1
