
- •preface
- •1.1 Introduction
- •1.5 Symmetric-key Encryption
- •1.6 Digital Signatures
- •1.8 Public-key cryptography
- •1.9 Hash Functions
- •1.11 Key Management
- •2.1 Probability Theory
- •2.2 Information Theory
- •2.3 Complexity Theory
- •2.4 Number Theory
- •2.5 Abstract Algebra
- •3.3 RSA Problem
- •3.8 Composite Moduli
- •4.1 Introduction
- •4.2 Primality Tests
- •4.5 Irreducible Polynomials
- •6. Stream Ciphers
- •7. Block Ciphers
- •8. Public-Key Encryption
- •10. Authentication
- •11. Digital Signatures
- •A.2 Crypto Proceedings
- •A.3 Eurocrypt Proceedings
- •References
- •Index

Chapter 8
|
Public-Key Encryption |
|
Contents in Brief |
|
|
8.1 |
Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
283 |
8.2 |
RSA public-key encryption . . . . . . . . . . . . . . . . . . . . . |
285 |
8.3 |
Rabin public-key encryption . . . . . . . . . . . . . . . . . . . . |
292 |
8.4 |
ElGamal public-key encryption . . . . . . . . . . . . . . . . . . . |
294 |
8.5 |
McEliece public-key encryption . . . . . . . . . . . . . . . . . . |
298 |
8.6 |
Knapsack public-key encryption . . . . . . . . . . . . . . . . . . |
300 |
8.7 |
Probabilistic public-key encryption . . . . . . . . . . . . . . . . . |
306 |
8.8 |
Notes and further references . . . . . . . . . . . . . . . . . . . . |
312 |
8.1 Introduction
This chapter considers various techniques for public-key encryption, also referred to as asymmetric encryption. As introduced previously (§1.8.1), in public-key encryption systems each entity A has a public key e and a corresponding private key d. In secure systems, the task of computing dgiven eis computationally infeasible. The public key defines an encryption transformation Ee, while the private key defines the associated decryption transformation Dd. Any entity B wishing to send a message m to A obtains an authentic copy of A’s public key e, uses the encryption transformation to obtain the ciphertext c = Ee(m), and transmits c to A. To decrypt c, A applies the decryption transformation to obtain the original message m = Dd(c).
The public key need not be kept secret, and, in fact, may be widely available – only its authenticity is required to guarantee that A is indeed the only party who knows the corresponding private key. A primary advantage of such systems is that providing authentic public keys is generally easier than distributing secret keys securely, as required in symmetrickey systems.
The main objective of public-key encryption is to provide privacy or confidentiality. Since A’s encryption transformation is public knowledge, public-key encryption alone does not provide data origin authentication (Definition 9.76) or data integrity (Definition 9.75). Such assurances must be provided through use of additional techniques (see §9.6), including message authentication codes and digital signatures.
Public-key encryption schemes are typically substantially slower than symmetric-key encryption algorithms such as DES (§7.4). For this reason, public-key encryption is most commonly used in practice for the transport of keys subsequently used for bulk data encryption by symmetric algorithms and other applications including data integrity and authentication, and for encrypting small data items such as credit card numbers and PINs.
283

284 |
Ch. 8 Public-Key Encryption |
Public-key decryption may also provide authentication guarantees in entity authentication and authenticated key establishment protocols.
Chapter outline
The remainder of the chapter is organized as follows. §8.1.1 provides introductory material. The RSA public-key encryption scheme is presented in §8.2; related security and implementation issues are also discussed. Rabin’s public-key encryption scheme, which is provably as secure as factoring, is the topic of §8.3. §8.4 considers the ElGamal encryption scheme; related security and implementation issues are also discussed. The McEliece public-key encryption scheme, based on error-correcting codes, is examined in §8.5. Although known to be insecure, the Merkle-Hellman knapsack public-key encryption scheme is presented in §8.6 for historical reasons – it was the first concrete realization of a public-key encryption scheme. Chor-Rivest encryption is also presented (§8.6.2) as an example of an as-yet unbroken public-key encryption scheme based on the subset sum (knapsack) problem. §8.7 introduces the notion of probabilistic public-key encryption, designed to meet especially stringent security requirements. §8.8 concludes with Chapter notes and references.
The number-theoretic computational problems which form the security basis for the public-key encryption schemes discussed in this chapter are listed in Table 8.1.
public-key encryption scheme |
computational problem |
|
|
RSA |
integer factorization problem (§3.2) |
|
RSA problem (§3.3) |
Rabin |
integer factorization problem (§3.2) |
|
square roots modulo composite n (§3.5.2) |
ElGamal |
discrete logarithm problem (§3.6) |
|
Diffie-Hellman problem (§3.7) |
generalized ElGamal |
generalized discrete logarithm problem (§3.6) |
|
generalized Diffie-Hellman problem (§3.7) |
McEliece |
linear code decoding problem |
Merkle-Hellman knapsack |
subset sum problem (§3.10) |
Chor-Rivest knapsack |
subset sum problem (§3.10) |
Goldwasser-Micali probabilistic |
quadratic residuosity problem (§3.4) |
Blum-Goldwasser probabilistic |
integer factorization problem (§3.2) |
|
Rabin problem (§3.9.3) |
Table 8.1: Public-key encryption schemes discussed in this chapter, and the related computational problems upon which their security is based.
8.1.1 Basic principles
Objectives of adversary
The primary objective of an adversary who wishes to “attack” a public-key encryption scheme is to systematically recover plaintext from ciphertext intended for some other entity A. If this is achieved, the encryption scheme is informally said to have been broken. A more ambitious objective is key recovery – to recover A’s private key. If this is achieved, the en-

§8.2 RSA public-key encryption |
285 |
cryption scheme is informally said to have been completely broken since the adversary then has the ability to decrypt all ciphertext sent to A.
Types of attacks
Since the encryption transformations are public knowledge, a passive adversary can always mount a chosen-plaintext attack on a public-key encryption scheme (cf. §1.13.1). A stronger attack is a chosen-ciphertext attack where an adversary selects ciphertext of its choice, and then obtains by some means (from the victim A) the corresponding plaintext (cf. §1.13.1). Two kinds of these attacks are usually distinguished.
1.In an indifferent chosen-ciphertext attack, the adversary is provided with decryptions of any ciphertexts of its choice, but these ciphertexts must be chosen prior to receiving the (target) ciphertext c it actually wishes to decrypt.
2.In an adaptive chosen-ciphertext attack, the adversary may use (or have access to) A’s decryption machine (but not the private key itself) even after seeing the target ciphertext c. The adversary may request decryptions of ciphertext which may be related to both the target ciphertext, and to the decryptions obtained from previous queries; a restriction is that it may not request the decryption of the target c itself.
Chosen-ciphertext attacks are of concern if the environment in which the public-key encryption scheme is to be used is subject to such an attack being mounted; if not, the existence of a chosen-ciphertext attack is typically viewed as a certificational weakness against a particular scheme, although apparently not directly exploitable.
Distributing public keys
The public-key encryption schemes described in this chapter assume that there is a means for the sender of a message to obtain an authentic copy of the intended receiver’s public key. In the absence of such a means, the encryption scheme is susceptible to an impersonation attack, as outlined in §1.8.2. There are many techniques in practice by which authentic public keys can be distributed, including exchanging keys over a trusted channel, using a trusted public file, using an on-line trusted server, and using an off-line server and certificates. These and related methods are discussed in §13.4.
Message blocking
Some of the public-key encryption schemes described in this chapter assume that the message to be encrypted is, at most, some fixed size (bitlength). Plaintext messages longer than this maximum must be broken into blocks, each of the appropriate size. Specific techniques for breaking up a message into blocks are not discussed in this book. The component blocks can then be encrypted independently (cf. ECB mode in §7.2.2(i)). To provide protection against manipulation (e.g., re-ordering) of the blocks, the Cipher Block Chaining (CBC) mode may be used (cf. §7.2.2(ii) and Example 9.84). Since the CFB and OFB modes (cf. §7.2.2(iii) and §7.2.2(iv)) employ only single-block encryption (and not decryption) for both message encryption and decryption, they cannot be used with public-key encryption schemes.
8.2 RSA public-key encryption
The RSA cryptosystem, named after its inventors R. Rivest, A. Shamir, and L. Adleman, is the most widely used public-key cryptosystem. It may be used to provide both secrecy and digital signatures and its security is based on the intractability of the integer factorization

286 |
Ch. 8 Public-Key Encryption |
problem (§3.2). This section describes the RSA encryption scheme, its security, and some implementation issues; the RSA signature scheme is covered in §11.3.1.
8.2.1Description
8.1Algorithm Key generation for RSA public-key encryption
SUMMARY: each entity creates an RSA public key and a corresponding private key. Each entity A should do the following:
1.Generate two large random (and distinct) primes pand q, each roughly the same size.
2.Compute n = pq and φ = (p − 1)(q − 1). (See Note 8.5.)
3.Select a random integer e, 1 < e < φ, such that gcd(e,φ) = 1.
4.Use the extended Euclidean algorithm (Algorithm 2.107) to compute the unique integer d, 1 < d < φ, such that ed ≡ 1 (mod φ).
5.A’s public key is (n,e); A’s private key is d.
8.2Definition The integers eand din RSA key generation are called the encryption exponent and the decryption exponent, respectively, while n is called the modulus.
8.3Algorithm RSA public-key encryption
SUMMARY: B encrypts a message m for A, which A decrypts.
1.Encryption. B should do the following:
(a)Obtain A’s authentic public key (n,e).
(b)Represent the message as an integer m in the interval [0,n − 1].
(c)Compute c = me mod n (e.g., using Algorithm 2.143).
(d)Send the ciphertext c to A.
2.Decryption. To recover plaintext m from c, A should do the following:
(a)Use the private key d to recover m = cd mod n.
Proof that decryption works. Since ed ≡ 1 (mod φ), there exists an integer k such that ed = 1 + kφ. Now, if gcd(m,p) = 1 then by Fermat’s theorem (Fact 2.127),
mp−1 ≡ 1 (mod p).
Raising both sides of this congruence to the power k(q−1)and then multiplying both sides by m yields
m1+k(p−1)(q−1) ≡ m (mod p).
On the other hand, if gcd(m,p) = p, then this last congruence is again valid since each side is congruent to 0 modulo p. Hence, in all cases
med ≡ m |
(mod p). |
By the same argument, |
|
med ≡ m |
(mod q). |
Finally, since p and q are distinct primes, it follows that med ≡ m (mod n),

§8.2 RSA public-key encryption |
287 |
and, hence,
cd ≡ (me)d ≡ m (mod n).
8.4Example (RSA encryption with artificially small parameters)
Key generation. Entity A chooses the primes p = 2357, q = 2551, and computes n = pq = 6012707and φ = (p−1)(q−1) = 6007800. A chooses e = 3674911and, using the extended Euclidean algorithm, finds d = 422191 such that ed ≡ 1 (mod φ). A’s public key is the pair (n = 6012707,e = 3674911), while A’s private key is d = 422191.
Encryption. To encrypt a message m = 5234673, B uses an algorithm for modular exponentiation (e.g., Algorithm 2.143) to compute
c = me mod n = 52346733674911 mod 6012707 = 3650502, |
|
and sends this to A. |
|
Decryption. To decrypt c, A computes |
|
cd mod n = 3650502422191 mod 6012707 = 5234673. |
|
8.5Note (universal exponent) The number λ = lcm(p−1,q −1), sometimes called the universal exponent of n, may be used instead of φ = (p − 1)(q − 1) in RSA key generation (Algorithm 8.1). Observe that λ is a proper divisor of φ. Using λ can result in a smaller decryption exponent d, which may result in faster decryption (cf. Note 8.9). However, if p and q are chosen at random, then gcd(p−1,q−1)is expected to be small, and consequently φ and λ will be roughly of the same size.
8.2.2Security of RSA
This subsection discusses various security issues related to RSA encryption. Various attacks which have been studied in the literature are presented, as well as appropriate measures to counteract these threats.
(i) Relation to factoring
The task faced by a passive adversary is that of recovering plaintext mfrom the corresponding ciphertext c, given the public information (n,e) of the intended receiver A. This is called the RSA problem (RSAP), which was introduced in §3.3. There is no efficient algorithm known for this problem.
One possible approach which an adversary could employ to solving the RSA problem is to first factor n, and then compute φ and d just as A did in Algorithm 8.1. Once d is obtained, the adversary can decrypt any ciphertext intended for A.
On the other hand, if an adversary could somehow compute d, then it could subsequently factor n efficiently as follows. First note that since ed ≡ 1 (mod φ), there is an integer k such that ed − 1 = kφ. Hence, by Fact 2.126(i), aed−1 ≡ 1 (mod n) for all a Zn. Let ed − 1 = 2st, where t is an odd integer. Then it can be shown that there exists an i [1,s] such that a2i−1t ≡1±(mod n) and a2it ≡ 1 (mod n) for at least half of all a Zn; if a and i are such integers then gcd(a2i−1t − 1,n) is a non-trivial factor of n. Thus the adversary simply needs to repeatedly select random a Zn and check if an i [1,s] satisfying the above property exists; the expected number of trials before a non-trivial factor of n is obtained is 2. This discussion establishes the following.
8.6Fact The problem of computing the RSA decryption exponent dfrom the public key (n,e), and the problem of factoring n, are computationally equivalent.

288 |
Ch. 8 Public-Key Encryption |
When generating RSA keys, it is imperative that the primes p and q be selected in such a way that factoring n = pq is computationally infeasible; see Note 8.8 for more details.
(ii) Small encryption exponent e
In order to improve the efficiency of encryption, it is desirable to select a small encryption exponent e (see Note 8.9) such as e = 3. A group of entities may all have the same encryption exponent e, however, each entity in the group must have its own distinct modulus (cf. §8.2.2(vi)). If an entity A wishes to send the same message m to three entities whose public moduli are n1, n2, n3, and whose encryption exponents are e = 3, then A would send ci = m3 mod ni, for i = 1,2,3. Since these moduli are most likely pairwise relatively prime, an eavesdropper observing c1, c2, c3 can use Gauss’s algorithm (Algorithm 2.121) to find a solution x, 0 ≤ x < n1n2n3, to the three congruences
x ≡ c1 x ≡ c2 x ≡ c3
(mod n1) (mod n2) (mod n3).
Since m3 < n1n2n3, by the Chinese remainder theorem (Fact 2.120), it must be the case that x = m3. Hence, by computing the integer cube root of x, the eavesdropper can recover the plaintext m.
Thus a small encryption exponent such as e = 3 should not be used if the same message, or even the same message with known variations, is sent to many entities. Alternatively, to prevent against such an attack, a pseudorandomly generated bitstring of appropriate length (taking into account Coppersmith’s attacks mentioned on pages 313–314) should be appended to the plaintext message prior to encryption; the pseudorandom bitstring should be independently generated for each encryption. This process is sometimes referred to as salting the message.
Small encryption exponents are also a problem for small messages m, because if m < n1/e, then m can be recovered from the ciphertext c = me mod n simply by computing the integer eth root of c; salting plaintext messages also circumvents this problem.
(iii) Forward search attack
If the message space is small or predictable, an adversary can decrypt a ciphertext cby simply encrypting all possible plaintext messages until c is obtained. Salting the message as described above is one simple method of preventing such an attack.
(iv) Small decryption exponent d
As was the case with the encryption exponent e, it may seem desirable to select a small decryption exponent din order to improve the efficiency of decryption. 1 However, if gcd(p− 1,q − 1) is small, as is typically the case, and if d has up to approximately one-quarter as many bits as the modulus n, then there is an efficient algorithm (referenced on page 313) for computing d from the public information (n,e). This algorithm cannot be extended to the case where d is approximately the same size as n. Hence, to avoid this attack, the decryption exponent d should be roughly the same size as n.
(v) Multiplicative properties
Let m1 and m2 be two plaintext messages, and let c1 and c2 be their respective RSA encryptions. Observe that
(m1m2)e ≡ me1me2 ≡ c1c2 (mod n).
1In this case, one would select d first and then compute e in Algorithm 8.1, rather than vice-versa.

§8.2 RSA public-key encryption |
289 |
In other words, the ciphertext corresponding to the plaintext m = m1m2 mod n is c = c1c2 mod n; this is sometimes referred to as the homomorphic property of RSA. This observation leads to the following adaptive chosen-ciphertext attack on RSA encryption.
Suppose that an active adversary wishes to decrypt a particular ciphertext c = me mod n intended for A. Suppose also that A will decrypt arbitrary ciphertext for the adversary, other than c itself. The adversary can conceal c by selecting a random integer x Zn
and computing c = cxe mod n. Upon presentation of c, A will compute for the adversary m = (c)d mod n. Since
m ≡ (c)d ≡ cd(xe)d ≡ mx (mod n),
the adversary can then compute m = mx−1 mod n.
This adaptive chosen-ciphertext attack should be circumvented in practice by imposing some structural constraints on plaintext messages. If a ciphertext cis decrypted to a message not possessing this structure, then c is rejected by the decryptor as being fraudulent. Now, if a plaintext message m has this (carefully chosen) structure, then with high probability mx mod n will not for x Zn. Thus the adaptive chosen-ciphertext attack described in the previous paragraph will fail because A will not decrypt c for the adversary. Note 8.63 provides a powerful technique for guarding against adaptive chosen-ciphertext and other kinds of attacks.
(vi) Common modulus attack
The following discussion demonstrates why it is imperative for each entity to choose its own RSA modulus n.
It is sometimes suggested that a central trusted authority should select a single RSA modulus n, and then distribute a distinct encryption/decryption exponent pair (ei,di) to each entity in a network. However, as shown in (i) above, knowledge of any (ei,di)pair allows for the factorization of the modulus n, and hence any entity could subsequently determine the decryption exponents of all other entities in the network. Also, if a single message were encrypted and sent to two or more entities in the network, then there is a technique by which an eavesdropper (any entity not in the network) could recover the message with high probability using only publicly available information.
(vii) Cycling attacks
Let c = me mod n be a ciphertext. Let k be a positive integer such that cek ≡ c (mod n); since encryption is a permutation on the message space {0,1,... ,n − 1} such an integer k must exist. For the same reason it must be the case that cek−1 ≡ m (mod n). This observation leads to the following cycling attack on RSA encryption. An adversary computes ce mod n, ce2 mod n, ce3 mod n,... until c is obtained for the first time. If cek mod n = c, then the previous number in the cycle, namely cek−1 mod n, is equal to the plaintext m.
A generalized cycling attack is to find the smallest positive integer u such that f = gcd(ceu − c,n) > 1. If
ceu ≡ c |
(mod p) and |
ceu ≡c |
(mod q) |
(8.1) |
then f = p. Similarly, if |
|
|
|
|
ceu ≡c |
(mod p) and |
ceu ≡ c |
(mod q) |
(8.2) |
then f = q. In either case, n has been factored, and the adversary can recover d and then m. On the other hand, if both
ceu ≡ c (mod p) and ceu ≡ c (mod q), |
(8.3) |

290 |
Ch. 8 Public-Key Encryption |
then f = n and ceu |
≡ c (mod n). In fact, u must be the smallest positive integer k |
for which cek ≡ c (mod n). In this case, the basic cycling attack has succeeded and so m = ceu−1 mod n can be computed efficiently. Since (8.3) is expected to occur much less frequently than (8.1) or (8.2), the generalized cycling attack usually terminates before the cycling attack does. For this reason, the generalized cycling attack can be viewed as being essentially an algorithm for factoring n.
Since factoring nis assumed to be intractable, these cycling attacks do not pose a threat to the security of RSA encryption.
(viii) Message concealing
A plaintext message m, 0 ≤ m ≤ n−1, in the RSA public-key encryption scheme is said to be unconcealed if it encrypts to itself; that is, me ≡ m (mod n). There are always some messages which are unconcealed (for example m = 0, m = 1, and m = n − 1). In fact, the number of unconcealed messages is exactly
[1 + gcd(e − 1,p − 1)] ·[1 + gcd(e − 1,q − 1)].
Since e−1, p−1 and q−1 are all even, the number of unconcealed messages is always at least 9. If p and q are random primes, and if e is chosen at random (or if e is chosen to be a small number such as e = 3 or e = 216 + 1 = 65537), then the proportion of messages which are unconcealed by RSA encryption will, in general, be negligibly small, and hence unconcealed messages do not pose a threat to the security of RSA encryption in practice.
8.2.3 RSA encryption in practice
There are numerous ways of speeding up RSA encryption and decryption in software and hardware implementations. Some of these techniques are covered in Chapter 14, including fast modular multiplication (§14.3), fast modular exponentiation (§14.6), and the use of the Chinese remainder theorem for faster decryption (Note 14.75). Even with these improvements, RSA encryption/decryption is substantially slower than the commonly used symmetric-key encryption algorithms such as DES (Chapter 7). In practice, RSA encryption is most commonly used for the transport of symmetric-key encryption algorithm keys and for the encryption of small data items.
The RSA cryptosystem has been patented in the U.S. and Canada. Several standards organizations have written, or are in the process of writing, standards that address the use of the RSA cryptosystem for encryption, digital signatures, and key establishment. For discussion of patent and standards issues related to RSA, see Chapter 15.
8.7Note (recommended size of modulus) Given the latest progress in algorithms for factoring integers (§3.2), a 512-bit modulus nprovides only marginal security from concerted attack. As of 1996, in order to foil the powerful quadratic sieve (§3.2.6) and number field sieve (§3.2.7) factoring algorithms, a modulus n of at least 768 bits is recommended. For longterm security, 1024-bit or larger moduli should be used.
8.8Note (selecting primes)
(i)As mentioned in §8.2.2(i), the primes p and q should be selected so that factoring n = pq is computationally infeasible. The major restriction on p and q in order to avoid the elliptic curve factoring algorithm (§3.2.4) is that p and q should be about the same bitlength, and sufficiently large. For example, if a 1024-bit modulus n is to be used, then each of p and q should be about 512 bits in length.
§8.2 RSA public-key encryption |
291 |
(ii) Another restriction on the primes p and q is that the difference p − q should not be |
|||||
too small. If p − q is small, then p ≈ q and hence p ≈ |
√ |
|
. Thus,√ |
n |
could be |
|
n |
||||
factored efficiently simply by trial division by all odd integers close to n. If p and q are chosen at random, then p − q will be appropriately large with overwhelming probability.
(iii)In addition to these restrictions, many authors have recommended that p and q be strong primes. A prime p is said to be a strong prime (cf. Definition 4.52) if the following three conditions are satisfied:
(a)p − 1 has a large prime factor, denoted r;
(b)p + 1 has a large prime factor; and
(c)r − 1 has a large prime factor.
An algorithm for generating strong primes is presented in §4.4.2. The reason for condition (a) is to foil Pollard’s p−1factoring algorithm (§3.2.3) which is efficient only if n has a prime factor p such that p − 1 is smooth. Condition (b) foils the p + 1 factoring algorithm mentioned on page 125 in §3.12, which is efficient only if n has a prime factor p such that p + 1 is smooth. Finally, condition (c) ensures that the cycling attacks described in §8.2.2(vii) will fail.
If the prime p is randomly chosen and is sufficiently large, then both p−1 and p+1 can be expected to have large prime factors. In any case, while strong primes protect against the p−1 and p+1factoring algorithms, they do not protect against their generalization, the elliptic curve factoring algorithm (§3.2.4). The latter is successful in factoring n if a randomly chosen number of the same size as p (more precisely, this number is the order of a randomly selected elliptic curve defined over Zp) has only small prime factors. Additionally, it has been shown that the chances of a cycling attack succeeding are negligible if p and q are randomly chosen (cf. §8.2.2(vii)). Thus, strong primes offer little protection beyond that offered by random primes. Given the current state of knowledge of factoring algorithms, there is no compelling reason for requiring the use of strong primes in RSA key generation. On the other hand, they are no less secure than random primes, and require only minimal additional running time to compute; thus there is little real additional cost in using them.
8.9Note (small encryption exponents)
(i)If the encryption exponent e is chosen at random, then RSA encryption using the repeated square-and-multiply algorithm (Algorithm 2.143) takes k modular squarings and an expected k/2 (less with optimizations) modular multiplications, where k is the bitlength of the modulus n. Encryption can be sped up by selecting e to be small and/or by selecting e with a small number of 1’s in its binary representation.
(ii)The encryption exponent e = 3 is commonly used in practice; in this case, it is necessary that neither p−1nor q−1be divisible by 3. This results in a very fast encryp-
tion operation since encryption only requires 1 modular multiplication and 1 modular squaring. Another encryption exponent used in practice is e = 216 + 1 = 65537.
This number has only two 1’s in its binary representation, and so encryption using
the repeated square-and-multiply algorithm requires only 16 modular squarings and 1 modular multiplication. The encryption exponent e = 216 + 1 has the advantage over e = 3 in that it resists the kind of attack discussed in §8.2.2(ii), since it is unlikely the same message will be sent to 216+1recipients. But see also Coppersmith’s attacks mentioned on pages 313–314.

292 |
Ch. 8 Public-Key Encryption |
8.3 Rabin public-key encryption
A desirable property of any encryption scheme is a proof that breaking it is as difficult as solving a computational problem that is widely believed to be difficult, such as integer factorization or the discrete logarithm problem. While it is widely believed that breaking the RSA encryption scheme is as difficult as factoring the modulus n, no such equivalence has been proven. The Rabin public-key encryption scheme was the first example of a provably secure public-key encryption scheme – the problem faced by a passive adversary of recovering plaintext from some given ciphertext is computationally equivalent to factoring.
8.10Algorithm Key generation for Rabin public-key encryption
SUMMARY: each entity creates a public key and a corresponding private key. Each entity A should do the following:
1.Generate two large random (and distinct) primes pand q, each roughly the same size.
2.Compute n = pq.
3.A’s public key is n; A’s private key is (p,q).
8.11Algorithm Rabin public-key encryption
SUMMARY: B encrypts a message m for A, which A decrypts.
1.Encryption. B should do the following:
(a)Obtain A’s authentic public key n.
(b)Represent the message as an integer m in the range {0,1,... ,n − 1}.
(c)Compute c = m2 mod n.
(d)Send the ciphertext c to A.
2.Decryption. To recover plaintext m from c, A should do the following:
(a)Use Algorithm 3.44 to find the four square roots m1, m2, m3, and m4 of cmodulo n.2 (See also Note 8.12.)
(b)The message sent was either m1, m2, m3, or m4. A somehow (cf. Note 8.14) decides which of these is m.
8.12Note (finding square roots of c modulo n = pq when p ≡ q ≡ 3 (mod 4)) If p and q are both chosen to be ≡ 3 (mod 4), then Algorithm 3.44 for computing the four square roots of c modulo n simplifies as follows:
1.Use the extended Euclidean algorithm (Algorithm 2.107) to find integers aand b satisfying ap + bq = 1. Note that a and b can be computed once and for all during the key generation stage (Algorithm 8.10).
2.Compute r = c(p+1)/4 mod p.
3.Compute s = c(q+1)/4 mod q.
4.Compute x = (aps + bqr) mod n.
5.Compute y = (aps − bqr) mod n.
6.The four square roots of c modulo n are x, −x mod n, y, and −y mod n.
2In the very unlikely case that gcd(m,n) =, the1 ciphertext cdoes not have four distinct square roots modulo n, but rather only one or two.

§8.3 Rabin public-key encryption |
293 |
8.13Note (security of Rabin public-key encryption)
(i)The task faced by a passive adversary is to recover plaintext m from the corresponding ciphertext c. This is precisely the SQROOT problem of §3.5.2. Recall (Fact 3.46) that the problems of factoring n and computing square roots modulo n are computationally equivalent. Hence, assuming that factoring n is computationally intractable, the Rabin public-key encryption scheme is provably secure against a passive adversary.
(ii)While provably secure against a passive adversary, the Rabin public-key encryption
scheme succumbs to a chosen-ciphertext attack (but see Note 8.14(ii)). Such an at-
tack can be mounted as follows. The adversary selects a random integer m Zn and computes c = m2 mod n. The adversary then presents c to A’s decryption machine, which decrypts c and returns some plaintext y. Since A does not know m, and m is
randomly chosen, the plaintext y is not necessarily the same as m. With probability 12, y ≡m±mod n, in which case gcd(m−y,n) is one of the prime factors of n. If
y ≡ ±m mod n, then the attack is repeated with a new m.3
(iii)The Rabin public-key encryption scheme is susceptible to attacks similar to those on RSA described in §8.2.2(ii), §8.2.2(iii), and §8.2.2(v). As is the case with RSA, attacks (ii) and (iii) can be circumvented by salting the plaintext message, while attack
(v) can be avoided by adding appropriate redundancy prior to encryption.
8.14Note (use of redundancy)
(i)A drawback of Rabin’s public-key scheme is that the receiver is faced with the task of selecting the correct plaintext from among four possibilities. This ambiguity in decryption can easily be overcome in practice by adding prespecified redundancy to the original plaintext prior to encryption. (For example, the last 64 bits of the message may be replicated.) Then, with high probability, exactly one of the four square roots m1, m2, m3, m4 of a legitimate ciphertext c will possess this redundancy, and the receiver will select this as the intended plaintext. If none of the square roots of c possesses this redundancy, then the receiver should reject c as fraudulent.
(ii)If redundancy is used as above, Rabin’s scheme is no longer susceptible to the chosen-
ciphertext attack of Note 8.13(ii). If an adversary selects a message m having the required redundancy and gives c = m2 mod n to A’s decryption machine, with very high probability the machine will return the plaintext m itself to the adversary (since the other three square roots of cwill most likely not contain the required redundancy), providing no new information. On the other hand, if the adversary selects a message
m which does not contain the required redundancy, then with high probability none of the four square roots of c = m2 mod n will possess the required redundancy. In this case, the decryption machine will fail to decrypt c and thus will not provide a response to the adversary. Note that the proof of equivalence of breaking the modified scheme by a passive adversary to factoring is no longer valid. However, if the natural assumption is made that Rabin decryption is composed of two processes, the first which finds the four square roots of c mod n, and the second which selects the distinguished square root as the plaintext, then the proof of equivalence holds. Hence, Rabin public-key encryption, suitably modified by adding redundancy, is of great practical interest.
3This chosen-ciphertext attack is an execution of the constructive proof of the equivalence of factoring n and the SQROOT problem (Fact 3.46), where A’s decryption machine is used instead of the hypothetical polynomialtime algorithm for solving the SQROOT problem in the proof.

294 |
Ch. 8 Public-Key Encryption |
8.15Example (Rabin public-key encryption with artificially small parameters)
Key generation. Entity A chooses the primes p = 277, q = 331, and computes n = pq = 91687. A’s public key is n = 91687, while A’s private key is (p = 277,q = 331). Encryption. Suppose that the last six bits of original messages are required to be replicated prior to encryption (cf. Note 8.14(i)). In order to encrypt the 10-bit message m = 1001111001, B replicates the last six bits of m to obtain the 16-bit message
m = 1001111001111001, which in decimal notation is m = 40569. B then computes
c = m2 mod n = 405692 mod 91687 = 62111
and sends this to A.
Decryption. To decrypt c, A uses Algorithm 3.44 and her knowledge of the factors of n to compute the four square roots of c mod n:
m1 = 69654, m2 = 22033, m3 = 40569, m4 = 51118,
which in binary are
m1 |
= 10001000000010110, |
m2 |
= 101011000010001, |
m3 |
= 1001111001111001, |
m4 |
= 1100011110101110. |
Since only m3 has the required redundancy, A decrypts c to m3 and recovers the original message m = 1001111001.
8.16Note (efficiency) Rabin encryption is an extremely fast operation as it only involves a single modular squaring. By comparison, RSA encryption with e = 3 takes one modular multiplication and one modular squaring. Rabin decryption is slower than encryption, but comparable in speed to RSA decryption.
8.4ElGamal public-key encryption
The ElGamal public-key encryption scheme can be viewed as Diffie-Hellman key agreement (§12.6.1) in key transfer mode (cf. Note 8.23(i)). Its security is based on the intractability of the discrete logarithm problem (see §3.6) and the Diffie-Hellman problem (§3.7). The basic ElGamal and generalized ElGamal encryption schemes are described in this section.
8.4.1Basic ElGamal encryption
8.17Algorithm Key generation for ElGamal public-key encryption
SUMMARY: each entity creates a public key and a corresponding private key. Each entity A should do the following:
1.Generate a large random prime p and a generator α of the multiplicative group Zp of the integers modulo p (using Algorithm 4.84).
2.Select a random integer a, 1 ≤ a ≤ p − 2, and compute αa mod p (using Algorithm 2.143).
3.A’s public key is (p,α,αa); A’s private key is a.

§8.4 ElGamal public-key encryption |
295 |
8.18Algorithm ElGamal public-key encryption
SUMMARY: B encrypts a message m for A, which A decrypts.
1.Encryption. B should do the following:
(a)Obtain A’s authentic public key (p,α,αa).
(b)Represent the message as an integer m in the range {0,1,... ,p − 1}.
(c)Select a random integer k, 1 ≤ k ≤ p − 2.
(d)Compute γ = αk mod p and δ = m · (αa)k mod p.
(e)Send the ciphertext c = (γ,δ) to A.
2.Decryption. To recover plaintext m from c, A should do the following:
(a)Use the private key a to compute γp−1−a mod p (note: γp−1−a = γ−a =
α−ak).
(b)Recover m by computing (γ−a) · δ mod p.
Proof that decryption works. The decryption of Algorithm 8.18 allows recovery of original plaintext because
γ−a ·δ ≡ α−akmαak ≡ m (mod p).
8.19Example (ElGamal encryption with artificially small parameters)
Key generation. Entity A selects the prime p = 2357 and a generator α = 2 of Z2357. A chooses the private key a = 1751 and computes
αa mod p = 21751 mod 2357 = 1185.
A’s public key is (p = 2357,α = 2,αa = 1185).
Encryption. To encrypt a message m = 2035, B selects a random integer k = 1520 and computes
γ = 21520 mod 2357 = 1430
and |
|
δ = 2035 ·11851520 mod 2357 = 697. |
|
B sends γ = 1430 and δ = 697 to A. |
|
Decryption. To decrypt, A computes |
|
γp−1−a = 1430605 mod 2357 = 872, |
|
and recovers m by computing |
|
m = 872 ·697 mod 2357 = 2035. |
|
8.20Note (common system-wide parameters) All entities may elect to use the same prime p and generator α, in which case p and α need not be published as part of the public key. This results in public keys of smaller sizes. An additional advantage of having a fixed base α is that exponentiation can then be expedited via precomputations using the techniques described in §14.6.3. A potential disadvantage of common system-wide parameters is that larger moduli p may be warranted (cf. Note 8.24).
296 |
Ch. 8 Public-Key Encryption |
8.21Note (efficiency of ElGamal encryption)
(i)The encryption process requires two modular exponentiations, namely αk mod pand (αa)k mod p. These exponentiations can be sped up by selecting random exponents k having some additional structure, for example, having low Hamming weights. Care must be taken that the possible number of exponents is large enough to preclude a search via a baby-step giant-step algorithm (cf. Note 3.59).
(ii)A disadvantage of ElGamal encryption is that there is message expansion by a factor of 2. That is, the ciphertext is twice as long as the corresponding plaintext.
8.22Remark (randomized encryption) ElGamal encryption is one of many encryption schemes which utilizes randomization in the encryption process. Others include McEliece encryption (§8.5), and Goldwasser-Micali (§8.7.1), and Blum-Goldwasser (§8.7.2) probabilistic encryption. Deterministic encryption schemes such as RSA may also employ randomization in order to circumvent some attacks (e.g., see §8.2.2(ii) and §8.2.2(iii)). The fundamental idea behind randomized encryption (see Definition 7.3) techniques is to use randomization to increase the cryptographic security of an encryption process through one or more of the following methods:
(i)increasing the effective size of the plaintext message space;
(ii)precluding or decreasing the effectiveness of chosen-plaintext attacks by virtue of a one-to-many mapping of plaintext to ciphertext; and
(iii)precluding or decreasing the effectiveness of statistical attacks by leveling the a priori probability distribution of inputs.
8.23Note (security of ElGamal encryption)
(i)The problem of breaking the ElGamal encryption scheme, i.e., recovering m given p, α, αa, γ, and δ, is equivalent to solving the Diffie-Hellman problem (see §3.7). In
fact, the ElGamal encryption scheme can be viewed as simply comprising a DiffieHellman key exchange to determine a session key αak, and then encrypting the message by multiplication with that session key. For this reason, the security of the El-
Gamal encryption scheme is said to be based on the discrete logarithm problem in Zp, although such an equivalence has not been proven.
(ii)It is critical that different random integers k be used to encrypt different messages. Suppose the same k is used to encrypt two messages m1 and m2 and the resulting ciphertext pairs are (γ1,δ1) and (γ2,δ2). Then δ1/δ2 = m1/m2, and m2 could be easily computed if m1 were known.
8.24Note (recommended parameter sizes) Given the latest progress on the discrete logarithm problem in Zp (§3.6), a 512-bit modulus p provides only marginal security from concerted attack. As of 1996, a modulus p of at least 768 bits is recommended. For long-term security, 1024-bit or larger moduli should be used. For common system-wide parameters (cf.
Note 8.20) even larger key sizes may be warranted. This is because the dominant stage in the index-calculus algorithm (§3.6.5) for discrete logarithms in Zp is the precomputation of a database of factor base logarithms, following which individual logarithms can be
computed relatively quickly. Thus computing the database of logarithms for one particular modulus p will compromise the secrecy of all private keys derived using p.

§8.4 ElGamal public-key encryption |
297 |
8.4.2 Generalized ElGamal encryption
The ElGamal encryption scheme is typically described in the setting of the multiplicative group Zp, but can be easily generalized to work in any finite cyclic group G.
As with ElGamal encryption, the security of the generalized ElGamal encryption scheme is based on the intractability of the discrete logarithm problem in the group G. The group G should be carefully chosen to satisfy the following two conditions:
1.for efficiency, the group operation in G should be relatively easy to apply; and
2.for security, the discrete logarithm problem in G should be computationally infeasible.
The following is a list of groups that appear to meet these two criteria, of which the first three have received the most attention.
1.The multiplicative group Zp of the integers modulo a prime p.
2.The multiplicative group F2m of the finite field F2m of characteristic two.
3.The group of points on an elliptic curve over a finite field.
4.The multiplicative group Fq of the finite field Fq, where q = pm, p a prime.
5.The group of units Zn, where n is a composite integer.
6.The jacobian of a hyperelliptic curve defined over a finite field.
7.The class group of an imaginary quadratic number field.
8.25Algorithm Key generation for generalized ElGamal public-key encryption
SUMMARY: each entity creates a public key and a corresponding private key. Each entity A should do the following:
1.Select an appropriate cyclic group Gof order n, with generator α. (It is assumed here that G is written multiplicatively.)
2.Select a random integer a, 1 ≤ a ≤ n − 1, and compute the group element αa.
3.A’s public key is (α,αa), together with a description of how to multiply elements in G; A’s private key is a.
8.26Algorithm Generalized ElGamal public-key encryption
SUMMARY: B encrypts a message m for A, which A decrypts.
1.Encryption. B should do the following:
(a)Obtain A’s authentic public key (α,αa).
(b)Represent the message as an element m of the group G.
(c)Select a random integer k, 1 ≤ k ≤ n − 1.
(d)Compute γ = αk and δ = m · (αa)k.
(e)Send the ciphertext c = (γ,δ) to A.
2.Decryption. To recover plaintext m from c, A should do the following:
(a)Use the private key a to compute γa and then compute γ−a.
(b)Recover m by computing (γ−a) · δ.
8.27Note (common system-wide parameters) All entities may elect to use the same cyclic group G and generator α, in which case α and the description of multiplication in G need not be published as part of the public key (cf. Note 8.20).

298 |
Ch. 8 Public-Key Encryption |
8.28Example (ElGamal encryption using the multiplicative group of F2m, with artificially small parameters)
Key generation. Entity Aselects the group Gto be the multiplicative group of the finite field
F24, whose elements are represented by the polynomials over F2 of degree less than 4, and where multiplication is performed modulo the irreducible polynomial f(x) = x4 + x + 1 (cf. Example 2.231). For convenience, a field element a3x3 + a2x2 + a1x + a0 is repre-
sented by the binary string (a3a2a1a0). The group G has order n = 15 and a generator is
α = (0010).
A chooses the private key a = 7 and computes αa = α7 = (1011). A’s public key is αa = (1011) (together with α = (0010) and the polynomial f(x) which defines the multiplication in G, if these parameters are not common to all entities).
Encryption. To encrypt a message m = (1100), B selects a random integer k = 11 and computes γ = α11 = (1110), (αa)11 = (0100), and δ = m · (αa)11 = (0101). B sends
γ = (1110) and δ = (0101) to A.
Decryption. To decrypt, A computes γa = (0100), (γa)−1 = (1101) and finally recovers m by computing m = (γ−a) · δ = (1100).
8.5 McEliece public-key encryption
The McEliece public-key encryption scheme is based on error-correcting codes. The idea behind this scheme is to first select a particular code for which an efficient decoding algorithm is known, and then to disguise the code as a general linear code (see Note 12.36). Since the problem of decoding an arbitrary linear code is NP-hard (Definition 2.73), a description of the original code can serve as the private key, while a description of the transformed code serves as the public key.
The McEliece encryption scheme (when used with Goppa codes) has resisted cryptanalysis to date. It is also notable as being the first public-key encryption scheme to use randomization in the encryption process. Although very efficient, the McEliece encryption scheme has received little attention in practice because of the very large public keys (see Remark 8.33).
8.29Algorithm Key generation for McEliece public-key encryption
SUMMARY: each entity creates a public key and a corresponding private key.
1.Integers k, n, and t are fixed as common system parameters.
2.Each entity A should perform steps 3 – 7.
3.Choose a k×n generator matrix G for a binary (n,k)-linear code which can correct t errors, and for which an efficient decoding algorithm is known. (See Note 12.36.)
4.Select a random k × k binary non-singular matrix S.
5.Select a random n × n permutation matrix P.
6.Compute the k × n matrix G = SGP.
7.A’s public key is (G,t); A’s private key is (S,G,P).

§8.5 McEliece public-key encryption |
299 |
8.30Algorithm McEliece public-key encryption
SUMMARY: B encrypts a message m for A, which A decrypts.
1.Encryption. B should do the following:
(a)Obtain A’s authentic public key (G,t).
(b)Represent the message as a binary string m of length k.
(c)Choose a random binary error vector z of length n having at most t 1’s.
(d)Compute the binary vector c = mG + z.
(e)Send the ciphertext c to A.
2.Decryption. To recover plaintext m from c, A should do the following:
(a)Compute c = cP−1, where P−1 is the inverse of the matrix P.
(b)Use the decoding algorithm for the code generated by G to decode c to m.
(c)Compute m = mS−1.
Proof that decryption works. Since
c = cP−1 = (mG + z)P−1 = (mSGP + z)P−1 = (mS)G + zP−1,
and zP−1 is a vector with at most t 1’s, the decoding algorithm for the code generated by G corrects c to m = mS. Finally, mS−1 = m, and, hence, decryption works.
A special type of error-correcting code, called a Goppa code, may be used in step 3 of the key generation. For each irreducible polynomial g(x)of degree tover F2m, there exists a binary Goppa code of length n = 2m and dimension k ≥ n − mt capable of correcting any pattern of t or fewer errors. Furthermore, efficient decoding algorithms are known for such codes.
8.31Note (security of McEliece encryption) There are two basic kinds of attacks known.
(i)From the public information, an adversary may try to compute the key G or a key G for a Goppa code equivalent to the one with generator matrix G. There is no efficient method known for accomplishing this.
(ii)An adversary may try to recover the plaintext mdirectly given some ciphertext c. The adversary picks k columns at random from G. If Gk, ck and zk denote the restriction of G, cand z, respectively, to these k columns, then (ck +zk) = mGk. If zk = 0 and
if Gk is non-singular, then m can be recovered by solving the system of equations ck = mGk. Since the probability that zk = 0, i.e., the selected k bits were not in
error, is only |
n−t |
/ |
n |
, the probability of this attack succeeding is negligibly small. |
|
k |
|
k |
|
8.32Note (recommended parameter sizes) The original parameters suggested by McEliece were n = 1024, t = 50, and k ≥ 524. Based on the security analysis (Note 8.31), an optimum choice of parameters for the Goppa code which maximizes the adversary’s work factor appears to be n = 1024, t = 38, and k ≥ 644.
8.33Remark (McEliece encryption in practice) Although the encryption and decryption operations are relatively fast, the McEliece scheme suffers from the drawback that the public key is very large. A (less significant) drawback is that there is message expansion by a factor of n/k. For the recommended parameters n = 1024, t = 38, k ≥ 644, the public key is about 219 bits in size, while the message expansion factor is about 1.6. For these reasons, the scheme receives little attention in practice.

300 |
Ch. 8 Public-Key Encryption |
8.6 Knapsack public-key encryption
Knapsack public-key encryption schemes are based on the subset sum problem, which is NP-complete (see §2.3.3 and §3.10). The basic idea is to select an instance of the subset sum problem that is easy to solve, and then to disguise it as an instance of the general subset sum problem which is hopefully difficult to solve. The original knapsack set can serve as the private key, while the transformed knapsack set serves as the public key.
The Merkle-Hellman knapsack encryption scheme (§8.6.1) is important for historical reasons, as it was the first concrete realization of a public-key encryption scheme. Many variations have subsequently been proposed but most, including the original, have been demonstrated to be insecure (see Note 8.40), a notable exception being the Chor-Rivest knapsack scheme (§8.6.2).
8.6.1 Merkle-Hellman knapsack encryption
The Merkle-Hellman knapsack encryption scheme attempts to disguise an easily solved instance of the subset sum problem, called a superincreasing subset sum problem, by modular multiplication and a permutation. It is however not recommended for use (see Note 8.40).
8.34 Definition A superincreasing sequence is a sequence (b1,b2,... ,bn)of positive integers with the property that bi > bj for each i, 2 ≤ i ≤ n.
Algorithm 8.35 efficiently solves the subset sum problem for superincreasing sequences.
8.35 Algorithm Solving a superincreasing subset sum problem
INPUT: a superincreasing sequence (b1,b2,... ,bn) and an integer s which is the sum of a
subset of the bi.
OUTPUT: (x1,x2,... ,xn) where xi {0,1}, such that ni=1 xibi = s.
1.i←n.
2.While i ≥ 1 do the following:
2.1If s ≥ bi then xi←1 and s←s − bi. Otherwise xi←0.
2.2i←i − 1.
3.Return((x1,x2,... ,xn)).
8.36Algorithm Key generation for basic Merkle-Hellman knapsack encryption
SUMMARY: each entity creates a public key and a corresponding private key.
1.An integer n is fixed as a common system parameter.
2.Each entity A should perform steps 3 – 7.
3.Choose a superincreasing sequence (b1,b2,... ,bn) and modulus M such that M > b1 + b2 + ···+ bn.
4.Select a random integer W, 1 ≤ W ≤ M − 1, such that gcd(W,M) = 1.
5.Select a random permutation π of the integers {1,2,... ,n}.
6.Compute ai = Wbπ(i) mod M for i = 1,2,... ,n.
7.A’s public key is (a1,a2,... ,an); A’s private key is (π,M,W,(b1,b2,... ,bn)).

§8.6 Knapsack public-key encryption |
301 |
8.37Algorithm Basic Merkle-Hellman knapsack public-key encryption
SUMMARY: B encrypts a message m for A, which A decrypts.
1.Encryption. B should do the following:
(a)Obtain A’s authentic public key (a1,a2,... ,an).
(b)Represent the message m as a binary string of length n, m = m1m2 ···mn.
(c)Compute the integer c = m1a1 + m2a2 + ···+ mnan.
(d)Send the ciphertext c to A.
2.Decryption. To recover plaintext m from c, A should do the following:
(a)Compute d = W−1c mod M.
(b)By solving a superincreasing subset sum problem (Algorithm 8.35), find integers r1,r2,... ,rn, ri {0,1}, such that d = r1b1 + r2b2 + ···+ rnbn.
(c)The message bits are mi = rπ(i), i = 1,2,... ,n.
Proof that decryption works. The decryption of Algorithm 8.37 allows recovery of original plaintext because
n |
n |
d ≡ W−1c ≡ W−1 miai ≡ |
mibπ(i) (mod M). |
i=1 |
i=1 |
Since 0 ≤ d < M, d = ni=1 mibπ(i) mod M, and hence the solution of the superincreasing subset sum problem in step (b) of the decryption gives the message bits, after application of the permutation π.
8.38Example (basic Merkle-Hellman knapsack encryption with artificially small parameters)
Key generation. Let n = 6. Entity A chooses the superincreasing sequence (12,17,33,74, 157,316), M = 737, W = 635, and the permutation π of {1,2,3,4,5,6} defined by
π(1) = 3, π(2) = 6, π(3) = 1, π(4) = 2, π(5) = 5, and π(6) = 4. A’s public key is the knapsack set (319,196,250,477,200,559), while A’s private key is (π,M,W,(12,17,33,
74,157,316)).
Encryption. To encrypt the message m = 101101, B computes
c = 319 + 250 + 477 + 559 = 1605
and sends this to A.
Decryption. To decrypt, A computes d = W−1c mod M = 136, and solves the superincreasing subset sum problem
136 = 12r1 + 17r2 + 33r3 + 74r4 + 157r5 + 316r6 |
|
to get 136 = 12 + 17 + 33 + 74. Hence, r1 = 1, r2 = 1, r3 = 1, r4 = 1, r5 = 0, r6 |
= 0, |
and application of the permutation π yields the message bits m1 = r3 = 1, m2 = r6 |
= 0, |
m3 = r1 = 1, m4 = r2 = 1, m5 = r5 = 0, m6 = r4 = 1. |
|
Multiple-iterated Merkle-Hellman knapsack encryption
One variation of the basic Merkle-Hellman scheme involves disguising the easy superincreasing sequence by a series of modular multiplications. The key generation for this variation is as follows.

302 |
Ch. 8 Public-Key Encryption |
8.39Algorithm Key generation for multiple-iterated Merkle-Hellman knapsack encryption
SUMMARY: each entity creates a public key and a corresponding private key.
1.Integers n and t are fixed as common system parameters.
2.Each entity A should perform steps 3 – 6.
3.Choose a superincreasing sequence (a(0)1 ,a(0)2 ,... ,a(0)n ).
4.For j from 1 to t do the following:
4.1Choose a modulus Mj with Mj > a(1j−1) + a(2j−1) + ··· + a(nj−1).
4.2Select a random integer Wj, 1 ≤ Wj ≤ Mj − 1, such that gcd(Wj,Mj) = 1.
4.3Compute a(ij) = a(ij−1)Wj mod Mj for i = 1,2,... ,n.
5.Select a random permutation π of the integers {1,2,... ,n}.
6.A’s public key is (a1,a2,... ,an), where ai = a(πt()i) for i = 1,2,... ,n; A’s private key is (π,M1,... ,Mt,W1,... ,Wt,a(0)1 ,a(0)2 ,... ,a(0)n ).
Encryption is performed in the same way as in the basic Merkle-Hellman scheme (Algorithm 8.37). Decryption is performed by successively computing dj = Wj−1dj+1 mod Mj for j = t,t−1,... ,1, where dt+1 = c. Finally, the superincreasing subset sum problem d1 = r1a(0)1 +r2a(0)2 +···+rna(0)n is solved for ri, and the message bits are recovered after application of the permutation π.
8.40 Note (insecurity of Merkle-Hellman knapsack encryption)
(i)A polynomial-time algorithm for breaking the basic Merkle-Hellman scheme is known. Given the public knapsack set, this algorithm finds a pair of integers U , M such that U /M is close to U/M (where W and M are part of the private key, and
U = W−1 mod M) and such that the integers bi = U ai mod M, 1 ≤ i ≤ n, form a superincreasing sequence. This sequence can then be used by an adversary in place of (b1,b2,... ,bn) to decrypt messages.
(ii)The most powerful general attack known on knapsack encryption schemes is the technique discussed in §3.10.2 which reduces the subset sum problem to the problem of finding a short vector in a lattice. It is typically successful if the density (see Definition 3.104) of the knapsack set is less than 0.9408. This is significant because the density of a Merkle-Hellman knapsack set must be less than 1, since otherwise there will in general be many subsets of the knapsack set with the same sum, in which case some ciphertexts will not be uniquely decipherable. Moreover, since each iteration in the multiple-iterated scheme lowers the density, this attack will succeed if the knapsack set has been iterated a sufficient number of times.
Similar techniques have since been used to break most knapsacks schemes that have been proposed, including the multiple-iterated Merkle-Hellman scheme. The most prominent knapsack scheme that has resisted such attacks to date is the Chor-Rivest scheme (but see Note 8.44).
8.6.2 Chor-Rivest knapsack encryption
The Chor-Rivest scheme is the only known knapsack public-key encryption scheme that does not use some form of modular multiplication to disguise an easy subset sum problem.

§8.6 Knapsack public-key encryption |
303 |
8.41Algorithm Key generation for Chor-Rivest public-key encryption
SUMMARY: each entity creates a public key and a corresponding private key. Each entity A should do the following:
1.Select a finite field Fq of characteristic p, where q = ph, p ≥ h, and for which the discrete logarithm problem is feasible (see Note 8.45(ii)).
2.Select a random monic irreducible polynomial f(x) of degree h over Zp (using Algorithm 4.70). The elements of Fq will be represented as polynomials in Zp[x] of degree less than h, with multiplication performed modulo f(x).
3.Select a random primitive element g(x) of the field Fq (using Algorithm 4.80).
4.For each ground field element i Zp, find the discrete logarithm ai = logg(x)(x+i) of the field element (x + i) to the base g(x).
5.Select a random permutation π on the set of integers {0,1,2,... ,p − 1}.
6.Select a random integer d, 0 ≤ d ≤ ph − 2.
7.Compute ci = (aπ(i) + d) mod (ph − 1) , 0 ≤ i ≤ p − 1.
8.A’s public key is ((c0,c1,... ,cp−1),p,h); A’s private key is (f(x),g(x),π,d).
8.42Algorithm Chor-Rivest public-key encryption
SUMMARY: B encrypts a message m for A, which A decrypts.
1.Encryption. B should do the following:
(a)Obtain A’s authentic public key ((c0,c1,... ,cp−1),p,h).
(b)Represent the message m as a binary string of length lg hp , where hp is a binomial coefficient (Definition 2.17).
(c)Consider m as the binary representation of an integer. Transform this integer into a binary vector M = (M0,M1,... ,Mp−1) of length p having exactly h 1’s as follows:
i.Set l←h.
ii.For i from 1 to p do the following:
If m ≥ p−l i then set Mi−1←1, m←m − p−l i , l←l − 1. Otherwise,
set Mi−1 |
←0. (Note: |
n |
= 1 for n ≥ 0; |
0 |
= 0 for l ≥ 1.) |
|
|
|
|
0 |
|
l |
|
(d) Compute c = |
p−1 |
Mici mod (ph − 1). |
|
|
||
|
i=0 |
|
|
|
|
|
(e)Send the ciphertext c to A.
2.Decryption. To recover plaintext m from c, A should do the following:
(a)Compute r = (c − hd) mod (ph − 1).
(b)Compute u(x) = g(x)r mod f(x) (using Algorithm 2.227).
(c)Compute s(x) = u(x) + f(x), a monic polynomial of degree h over Zp.
(d) Factor s(x) into linear factors over Zp: s(x) = |
h |
(x + tj), where tj Zp |
(cf. Note 8.45(iv)). |
j=1 |
|
|
|
(e)Compute a binary vector M = (M0,M1,... ,Mp−1) as follows. The components of M that are 1 have indices π−1(tj), 1 ≤ j ≤ h. The remaining components are 0.
(f)The message m is recovered from M as follows:
i.Set m←0, l←h.
ii.For i from 1 to p do the following:
If Mi−1 = 1 then set m←m + p−l i and l←l − 1.

304 Ch. 8 Public-Key Encryption
Proof that decryption works. Observe that |
|
||
u(x) = |
g(x)r mod f(x) |
|
|
≡ |
g(x)c−hd ≡ g(x)( |
ip=0−1 Mici)−hd |
(mod f(x)) |
≡ |
g(x)( ip=0−1 Mi(aπ(i)+d))−hd ≡ g(x) |
ip=0−1 Miaπ(i) (mod f(x)) |
|
|
p−1 |
p−1 |
|
≡ |
[g(x)aπ(i) ]Mi ≡ |
(x + π(i))Mi (mod f(x)). |
|
|
i=0 |
i=0 |
|
Since pi=0−1(x + π(i))Mi and s(x) are monic polynomials of degree h and are congruent modulo f(x), it must be the case that
p−1
s(x) = u(x) + f(x) = (x + π(i))Mi.
i=0
Hence, the hroots of s(x)all lie in Zp, and applying π−1 to these roots gives the coordinates of M that are 1.
8.43Example (Chor-Rivest public-key encryption with artificially small parameters)
Key generation. Entity A does the following:
1.Selects p = 7 and h = 4.
2.Selects the irreducible polynomial f(x) = x4 + 3x3 + 5x2 + 6x + 2 of degree 4
over Z7. The elements of the finite field F74 are represented as polynomials in Z7[x] of degree less than 4, with multiplication performed modulo f(x).
3.Selects the random primitive element g(x) = 3x3 + 3x2 + 6.
4.Computes the following discrete logarithms:
a0 = logg(x) a1 = logg(x) a2 = logg(x) a3 = logg(x) a4 = logg(x) a5 = logg(x) a6 = logg(x)
(x) = 1028
(x + 1) = 1935 (x + 2) = 2054 (x + 3) = 1008 (x + 4) = 379 (x + 5) = 1780 (x + 6) = 223.
5.Selects the random permutation π on {0,1,2,3,4,5,6}defined by π(0) = 6, π(1) = 4, π(2) = 0, π(3) = 2, π(4) = 1, π(5) = 5, π(6) = 3.
6.Selects the random integer d = 1702.
7.Computes
c0 = (a6 + d) mod 2400 = 1925 c1 = (a4 + d) mod 2400 = 2081 c2 = (a0 + d) mod 2400 = 330 c3 = (a2 + d) mod 2400 = 1356 c4 = (a1 + d) mod 2400 = 1237 c5 = (a5 + d) mod 2400 = 1082 c6 = (a3 + d) mod 2400 = 310.
§8.6 Knapsack public-key encryption |
305 |
8.A’s public key is ((c0,c1,c2,c3,c4,c5,c6),p = 7,h = 4), while A’s private key is
(f(x),g(x),π,d).
Encryption. To encrypt a message m = |
22 for A, B does the following: |
|
|
|
(a) |
Obtains authentic A’s public key. |
|
|
|
(b) |
Represents m as a binary string of length 5: m = 10110. (Note that lg |
7 |
= 5.) |
|
|
|
|
4 |
|
(c)Uses the method outlined in step 1(c) of Algorithm 8.42 to transform m to the binary vector M = (1,0,1,1,0,0,1)of length 7.
(d)Computes c = (c0 + c2 + c3 + c6) mod 2400 = 1521.
(e)Sends c = 1521 to A.
Decryption. To decrypt the ciphertext c = 1521, A does the following:
(a)Computes r = (c − hd) mod 2400 = 1913.
(b)Computes u(x) = g(x)1913 mod f(x) = x3 + 3x2 + 2x + 5.
(c)Computes s(x) = u(x) + f(x) = x4 + 4x3 + x2 + x.
(d)Factors s(x) = x(x + 2)(x + 3)(x + 6) (so t1 = 0, t2 = 2, t3 = 3, t4 = 6).
(e)The components of M that are 1 have indices π−1(0) = 2, π−1(2) = 3, π−1(3) = 6, and π−1(6) = 0. Hence, M = (1,0,1,1,0,0,1).
(f)Uses the method outlined in step 2(f) of Algorithm 8.42 to transform M to the integer
m = 22, thus recovering the original plaintext. |
|
8.44Note (security of Chor-Rivest encryption)
(i)When the parameters of the system are carefully chosen (see Note 8.45 and page 318), there is no feasible attack known on the Chor-Rivest encryption scheme. In particular, the density of the knapsack set (c0,c1,... ,cp−1) is p/lg(maxci), which is large enough to thwart the low-density attacks on the general subset sum problem (§3.10.2).
(ii)It is known that the system is insecure if portions of the private key are revealed, for example, if g(x) and d in some representation of Fq are known, or if f(x) is known, or if π is known.
8.45Note (implementation)
(i)Although the Chor-Rivest scheme has been described only for the case p a prime, it extends to the case where the base field Zp is replaced by a field of prime power order.
(ii)In order to make the discrete logarithm problem feasible in step 1 of Algorithm 8.41, the parameters p and h may be chosen so that q = ph − 1 has only small factors. In this case, the Pohlig-Hellman algorithm (§3.6.4) can be used to efficiently compute discrete logarithms in the finite field Fq.
(iii)In practice, the recommended size of the parameters are p ≈ 200 and h ≈ 25. One
particular choice of parameters originally suggested is p = 197 and h = 24; in this case, the largest prime factor of 19724 −1 is 10316017, and the density of the knapsack set is about 1.077. Other parameter sets originally suggested are {p = 211,h = 24}, {p = 35,h = 24} (base field F35), and {p = 28,h = 25} (base field F28).
(iv)Encryption is a very fast operation. Decryption is much slower, the bottleneck being the computation of u(x) in step 2b. The roots of s(x) in step 2d can be found simply by trying all possibilities in Zp.
(v)A major drawback of the Chor-Rivest scheme is that the public key is fairly large, namely, about (ph · lgp) bits. For the parameters p = 197 and h = 24, this is about
36000 bits.

306 Ch. 8 Public-Key Encryption
(vi) There is message expansion by a factor of lgph/lg |
p |
. For p = 197 and h = 24, |
this is 1.797. |
h |
|
|
|
8.7 Probabilistic public-key encryption
A minimal security requirement of an encryption scheme is that it must be difficult, in essentially all cases, for a passive adversary to recover plaintext from the corresponding ciphertext. However, in some situations, it may be desirable to impose more stringent security requirements.
The RSA, Rabin, and knapsack encryption schemes are deterministic in the sense that under a fixed public key, a particular plaintext mis always encrypted to the same ciphertext c. A deterministic scheme has some or all of the following drawbacks.
1.The scheme is not secure for all probability distributions of the message space. For example, in RSA the messages 0and 1always get encrypted to themselves, and hence are easy to detect.
2.It is sometimes easy to compute partial information about the plaintext from the ciphertext. For example, in RSA if c = me mod n is the ciphertext corresponding to a plaintext m, then
c |
|
= |
me |
= |
m e |
= |
m |
|
|
|
|
|
|
|
|||
n |
n |
n |
n |
|||||
since e is odd, and hence an adversary can easily gain one bit of information about m, namely the Jacobi symbol mn .
3. It is easy to detect when the same message is sent twice.
Of course, any deterministic encryption scheme can be converted into a randomized scheme by requiring that a portion of each plaintext consist of a randomly generated bitstring of a pre-specified length l. If the parameter l is chosen to be sufficiently large for the purpose at hand, then, in practice, the attacks listed above are thwarted. However, the resulting randomized encryption scheme is generally not provably secure against the different kinds of attacks that one could conceive.
Probabilistic encryption utilizes randomness to attain a provable and very strong level of security. There are two strong notions of security that one can strive to achieve.
8.46Definition A public-key encryption scheme is said to be polynomially secure if no passive adversary can, in expected polynomial time, select two plaintext messages m1 and m2 and
then correctly distinguish between encryptions of m1 and m2 with probability significantly greater than 12.
8.47Definition A public-key encryption scheme is said to be semantically secure if, for all probability distributions over the message space, whatever a passive adversary can compute in expected polynomial time about the plaintext given the ciphertext, it can also compute in expected polynomial time without the ciphertext.
Intuitively, a public-key encryption scheme is semantically secure if the ciphertext does not leak any partial information whatsoever about the plaintext that can be computed in expected polynomial time.

§8.7 Probabilistic public-key encryption |
307 |
8.48Remark (perfect secrecy vs. semantic security) In Shannon’s theory (see §1.13.3(i)), an encryption scheme has perfect secrecy if a passive adversary, even with infinite computational resources, can learn nothing about the plaintext from the ciphertext, except possibly its length. The limitation of this notion is that perfect secrecy cannot be achieved unless the key is at least as long as the message. By contrast, the notion of semantic security can be viewed as a polynomially bounded version of perfect secrecy — a passive adversary with polynomially bounded computational resources can learn nothing about the plaintext from the ciphertext. It is then conceivable that there exist semantically secure encryption schemes where the keys are much shorter that the messages.
Although Definition 8.47 appears to be stronger than Definition 8.46, the next result asserts that they are, in fact, equivalent.
8.49Fact A public-key encryption scheme is semantically secure if and only if it is polynomially secure.
8.7.1Goldwasser-Micali probabilistic encryption
The Goldwasser-Micali scheme is a probabilistic public-key system which is semantically secure assuming the intractability of the quadratic residuosity problem (see §3.4).
8.50Algorithm Key generation for Goldwasser-Micali probabilistic encryption
SUMMARY: each entity creates a public key and corresponding private key. Each entity A should do the following:
1.Select two large random (and distinct) primes p and q, each roughly the same size.
2.Compute n = pq.
3.Select a y Zn such that y is a quadratic non-residue modulo n and the Jacobi sym-
bol ny
= 1 (y is a pseudosquare modulo n); see Remark 8.54.
4.A’s public key is (n,y); A’s private key is the pair (p,q).
8.51Algorithm Goldwasser-Micali probabilistic public-key encryption
SUMMARY: B encrypts a message m for A, which A decrypts.
1.Encryption. B should do the following:
(a)Obtain A’s authentic public key (n,y).
(b)Represent the message m as a binary string m = m1m2 ···mt of length t.
(c)For i from 1 to t do:
i.Pick an x Zn at random.
ii.If mi = 1 then set ci←yx2 mod n; otherwise set ci←x2 mod n.
(d)Send the t-tuple c = (c1,c2,... ,ct) to A.
2.Decryption. To recover plaintext m from c, A should do the following:
(a)For i from 1 to t do:
i. Compute the Legendre symbol ei = |
ci |
(using Algorithm 2.149). |
|
p |
|
ii.If ei = 1 then set mi←0; otherwise set mi←1.
(b)The decrypted message is m = m1m2 ···mt.

308 Ch. 8 Public-Key Encryption
Proof that decryption works. If a message bit mi is 0, then ci = x2 mod n is a quadratic residue modulo n. If a message bit mi is 1, then since y is a pseudosquare modulo n, ci = yx2 mod n is also a pseudosquare modulo n. By Fact 2.137, ci is a quadratic residue
modulo n if and only if ci is a quadratic residue modulo p, or equivalently |
ci |
= 1. Since |
|
p |
|
A knows p, she can compute this Legendre symbol and hence recover the message bit mi.
8.52Note (security of Goldwasser-Micali probabilistic encryption) Since x is selected at random from Zn, x2 mod n is a random quadratic residue modulo n, and yx2 mod n is a random pseudosquare modulo n. Hence, an eavesdropper sees random quadratic residues and pseudosquares modulo n. Assuming that the quadratic residuosity problem is difficult, the eavesdropper can do no better that guess each message bit. More formally, if the quadratic residuosity problem is hard, then the Goldwasser-Micali probabilistic encryption scheme is semantically secure.
8.53Note (message expansion) A major disadvantage of the Goldwasser-Micali scheme is the message expansion by a factor of lgn bits. Some message expansion is unavoidable in a probabilistic encryption scheme because there are many ciphertexts corresponding to each plaintext. Algorithm 8.56 is a major improvement of the Goldwasser-Micali scheme in that the plaintext is only expanded by a constant factor.
8.54Remark (finding pseudosquares) A pseudosquare y modulo n can be found as follows. First find a quadratic non-residue a modulo p and a quadratic non-residue b modulo q (see Remark 2.151). Then use Gauss’s algorithm (Algorithm 2.121) to compute the integer y, 0 ≤ y ≤ n−1, satisfying the simultaneous congruences y ≡ a (mod p), y ≡ b (mod q). Since y (≡ a (mod p)) is a quadratic non-residue modulo p, it is also a quadratic nonresidue modulo n(Fact 2.137). Also, by the properties of the Legendre and Jacobi symbols
(§2.4.5), |
y |
= |
y |
y |
= (−1)(−1) = 1. Hence, y is a pseudosquare modulo n. |
|
n |
|
p |
q |
|
8.7.2 Blum-Goldwasser probabilistic encryption
The Blum-Goldwasser probabilistic public-key encryption scheme is the most efficient probabilistic encryption scheme known and is comparable to the RSA encryption scheme, both in terms of speed and message expansion. It is semantically secure (Definition 8.47) assuming the intractability of the integer factorization problem. It is, however, vulnerable to a chosen-ciphertext attack (see Note 8.58(iii)). The scheme uses the Blum-Blum-Shub generator (§5.5.2) to generate a pseudorandom bit sequence which is then XORed with the plaintext. The resulting bit sequence, together with an encryption of the random seed used, is transmitted to the receiver who uses his trapdoor information to recover the seed and subsequently reconstruct the pseudorandom bit sequence and the plaintext.
8.55Algorithm Key generation for Blum-Goldwasser probabilistic encryption
SUMMARY: each entity creates a public key and a corresponding private key. Each entity A should do the following:
1.Select two large random (and distinct) primes p, q, each congruent to 3 modulo 4.
2.Compute n = pq.
3.Use the extended Euclidean algorithm (Algorithm 2.107) to compute integers a and b such that ap + bq = 1.
4.A’s public key is n; A’s private key is (p,q,a,b).

§8.7 Probabilistic public-key encryption |
309 |
8.56Algorithm Blum-Goldwasser probabilistic public-key encryption
SUMMARY: B encrypts a message m for A, which A decrypts.
1.Encryption. B should do the following:
(a)Obtain A’s authentic public key n.
(b)Let k = lgn and h = lgk . Represent the message m as a string m = m1m2 ···mt of length t, where each mi is a binary string of length h.
(c)Select as a seed x0, a random quadratic residue modulo n. (This can be done by selecting a random integer r Zn and setting x0←r2 mod n.)
(d)For i from 1 to t do the following:
i.Compute xi = x2i−1 mod n.
ii.Let pi be the h least significant bits of xi.
iii.Compute ci = pi mi.
(e)Compute xt+1 = x2t mod n.
(f)Send the ciphertext c = (c1,c2,... ,ct,xt+1) to A.
2.Decryption. To recover plaintext m from c, A should do the following:
(a)Compute d1 = ((p + 1)/4)t+1 mod (p − 1).
(b)Compute d2 = ((q + 1)/4)t+1 mod (q − 1).
(c)Compute u = xdt+11 mod p.
(d)Compute v = xdt+12 mod q.
(e)Compute x0 = vap + ubq mod n.
(f)For i from 1 to t do the following:
i.Compute xi = x2i−1 mod n.
ii.Let pi be the h least significant bits of xi.
iii.Compute mi = pi ci.
Proof that decryption works. Since xt is a quadratic residue modulo n, it is also a quadratic residue modulo p; hence, x(tp−1)/2 ≡ 1 (mod p). Observe that
x(p+1)/4 |
≡ (x2)(p+1)/4 |
≡ x(p+1)/2 |
≡ x(p−1)/2xt ≡ xt (mod p). |
|||
t+1 |
t |
|
t |
|
|
t |
Similarly, xt(p+1)/4 ≡ xt−1 (mod p) and so |
|
|
||||
|
((p+1)/4)2 |
≡ xt−1 |
(mod p). |
|||
|
xt+1 |
|
||||
Repeating this argument yields |
|
|
|
|
|
|
|
u ≡ xd1 |
≡ x((p+1)/4)t+1 |
≡ x0 (mod p). |
|||
|
t+1 |
|
t+1 |
|
|
|
Analogously, |
|
|
|
|
|
|
|
v |
≡ xd2 |
≡ x0 |
|
(mod q). |
|
|
|
|
t+1 |
|
|
|
Finally, since ap + bq = 1, vap + ubq ≡ x0 |
(mod p) and vap + ubq ≡ x0 (mod q). |
|||||
Hence, x0 = vap + ubq mod n, and A recovers the same random seed that B used in the encryption, and consequently also recovers the original plaintext.
8.57Example (Blum-Goldwasser probabilistic encryption with artificially small parameters)
Key generation. Entity Aselects the primes p = 499, q = 547, each congruent to 3modulo 4, and computes n = pq = 272953. Using the extended Euclidean algorithm, A computes

310 Ch. 8 Public-Key Encryption
the integers a = −57, b = 52 satisfying ap+bq = 1. A’s public key is n = 272953, while A’s private key is (p,q,a,b).
Encryption. The parameters k and h have the values 18 and 4, respectively. B represents the message m as a string m1m2m3m4m5 (t = 5) where m1 = 1001, m2 = 1100, m3 = 0001, m4 = 0000, m5 = 1100. B then selects a random quadratic residue x0 = 159201 (= 3992 mod n), and computes:
i |
xi = xi2−1 mod n |
pi |
ci = pi mi |
|
|
|
|
1 |
180539 |
1011 |
0010 |
2 |
193932 |
1100 |
0000 |
3 |
245613 |
1101 |
1100 |
4 |
130286 |
1110 |
1110 |
5 |
40632 |
1000 |
0100 |
|
|
|
|
and x6 |
= x2 |
mod n = 139680. B sends the ciphertext |
|
|
|
|
5 |
|
|
|
|
|
|
c = (0010,0000,1100,1110,0100,139680) |
|||
to A. |
|
|
|
|
|
Decryption. To decrypt c, A computes |
|
|
|||
|
|
d1 |
= ((p + 1)/4)6 mod (p − 1) = |
463 |
|
|
|
d2 |
= ((q + 1)/4)6 mod (q − 1) = |
337 |
|
|
|
u = x6463 mod p |
= |
20 |
|
|
|
v = x6337 mod q |
= |
24 |
|
|
|
x0 |
= vap + ubq mod n |
= |
159201. |
Finally, A uses x0 to construct the xi and pi just as B did for encryption, and recovers the plaintext mi by XORing the pi with the ciphertext blocks ci.
8.58Note (security of Blum-Goldwasser probabilistic encryption)
(i)Observe first that n is a Blum integer (Definition 2.156). An eavesdropper sees the quadratic residue xt+1. Assuming that factoring n is difficult, the h least significant bits of the principal square root xt of xt+1 modulo n are simultaneously secure (see Definition 3.82 and Fact 3.89). Thus the eavesdropper can do no better than to guess the pseudorandom bits pi, 1 ≤ i ≤ t. More formally, if the integer factorization problem is hard, then the Blum-Goldwasser probabilistic encryption scheme is semantically secure. Note, however, that for a modulus n of a fixed bitlength (e.g., 1024 bits), this statement is no longer true, and the scheme should only be considered computationally secure.
(ii)As of 1996, the modulus n should be at least 1024bits in length if long-term security is desired (cf. Note 8.7). If n is a 1025-bit integer, then k = 1024 and h = 10.
(iii)As with the Rabin encryption scheme (Algorithm 8.11), the Blum-Goldwasser scheme is also vulnerable to a chosen-ciphertext attack that recovers the private key from the public key. It is for this reason that the Blum-Goldwasser scheme has not received much attention in practice.
8.59Note (efficiency of Blum-Goldwasser probabilistic encryption)
(i)Unlike Goldwasser-Micali encryption, the ciphertext in Blum-Goldwasser encryption is only longer than the plaintext by a constant number of bits, namely k+1 (the size in bits of the integer xt+1).

§8.7 Probabilistic public-key encryption |
311 |
(ii)The encryption process is quite efficient — it takes only 1 modular multiplication to encrypt h bits of plaintext. By comparison, the RSA encryption process (Algorithm 8.3) requires 1 modular exponentiation (me mod n) to encrypt k bits of plaintext. Assuming that the parameter e is randomly chosen and assuming that an (unoptimized) modular exponentiation takes 3k/2 modular multiplications, this translates to an encryption rate for RSA of 2/3 bits per modular multiplication. If one chooses a special value for e, such as e = 3 (see Note 8.9), then RSA encryption is faster than Blum-Goldwasser encryption.
(iii)Blum-Goldwasser decryption (step 2 of Algorithm 8.56) is also quite efficient, requiring 1 exponentiation modulo p−1(step 2a), 1 exponentiation modulo q−1(step 2b), 1 exponentiation modulo p(step 2c), 1 exponentiation modulo q (step 2d), and tmultiplications modulo n (step 2f) to decrypt ht ciphertext bits. (The time to perform step 2e is negligible.) By comparison, RSA decryption (step 2 of Algorithm 8.3) requires 1 exponentiation modulo n (which can be accomplished by doing 1 exponentiation modulo p and 1 exponentiation modulo q) to decrypt k ciphertext bits. Thus, for short messages (< k bits), Blum-Goldwasser decryption is slightly slower than RSA decryption, while for longer messages, Blum-Goldwasser is faster.
8.7.3Plaintext-aware encryption
While semantic security (Definition 8.47) is a strong security requirement for public-key encryption schemes, there are other measures of security.
8.60Definition A public-key encryption scheme is said to be non-malleable if given a ciphertext, it is computationally infeasible to generate a different ciphertext such that the respective plaintexts are related in a known manner.
8.61Fact If a public-key encryption scheme is non-malleable, it is also semantically secure.
Another notion of security is that of being plaintext-aware. In Definition 8.62, valid ciphertext means those ciphertext which are the encryptions of legitimate plaintext messages (e.g. messages containing pre-specified forms of redundancy).
8.62Definition A public-key encryption scheme is said to be plaintext-aware if it is computationally infeasible for an adversary to produce a valid ciphertext without knowledge of the corresponding plaintext.
In the “random oracle model”, the property of being plaintext-aware is a strong one
— coupled with semantic security, it can be shown to imply that the encryption scheme is non-malleable and also secure against adaptive chosen-ciphertext attacks. Note 8.63 gives one method of transforming any k-bit to k-bit trapdoor one-way permutation (such as RSA) into an encryption scheme that is plaintext-aware and semantically secure.
8.63Note (Bellare-Rogaway plaintext-aware encryption) Let f be a k-bit to k-bit trapdoor oneway permutation (such as RSA). Let k0 and k1 be parameters such that 2k0 and 2k1 steps
each represent infeasible amounts of work (e.g., k0 = k1 = 128). The length of the plaintext m is fixed to be n = k −k0 −k1 (e.g., for k = 1024, n = 768). Let G : {0,1}k0 −→ {0,1}n+k1 and H : {0,1}n+k1 −→ {0,1}k0 be random functions. Then the encryption function, as depicted in Figure 8.1, is
E(m) = f({m0k1 G(r)} {r H(m0k1 G(r))}),
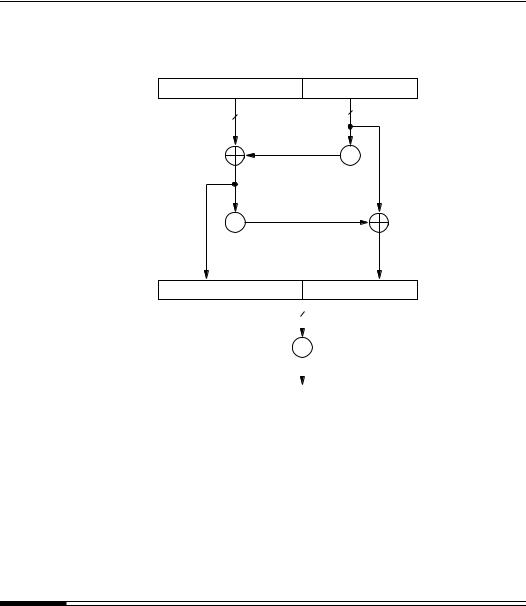
312 Ch. 8 Public-Key Encryption
where m0k1 denotes m concatenated with a string of 0’s of bitlength k1, r is a random binary string of bitlength k0, and denotes concatenation.
m0k1 |
r |
n + k1 |
k0 |
|
|
|
G |
H
m0k1 G(r) |
|
r H(m0k1 G(r)) |
|
n + k0 + k1 |
|
m plaintext |
|
|
|
|
|
|
|
|
r random bit string |
|
f |
||
|
E(m) ciphertext |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
E(m) |
|
|
Figure 8.1: Bellare-Rogaway plaintext-aware encryption scheme.
Under the assumption that Gand H are random functions, the encryption scheme E of Note 8.63 can be proven to be plaintext-aware and semantically secure. In practice, G and H can be derived from a cryptographic hash function such as the Secure Hash Algorithm (§9.4.2(iii)). In this case, the encryption scheme can no longer be proven to be plaintextaware because the random function assumption is not true; however, such a scheme appears to provides greater security assurances than those designed using ad hoc techniques.
8.8 Notes and further references
§8.1
For an introduction to public-key cryptography and public-key encryption in particular, see §1.8. A particularly readable introduction is the survey by Diffie [343]. Historical notes on public-key cryptography are given in the notes to §1.8 on page 47. A comparison of the features of public-key and symmetric-key encryption is given in §1.8.4; see also §13.2.5.
Other recent proposals for public-key encryption schemes include those based on finite automata (Renji [1032]); hidden field equations (Patarin [965]); and isomorphism of polynomials (Patarin [965]).
§8.2
The RSA cryptosystem was invented in 1977 by Rivest, Shamir, and Adleman [1060]. Kaliski and Robshaw [655] provide an overview of the major attacks on RSA encryption and
§8.8 Notes and further references |
313 |
signatures, and the practical methods of counteracting these threats.
The computational equivalence of computing the decryption exponent d and factoring n (§8.2.2(i)) was shown by Rivest, Shamir and Adleman [1060], based on earlier work by Miller [876].
The attack on RSA with small encryption exponent (§8.2.2(ii)) is discussed by H˚astad [544], who showed more generally that sending the encryptions of more than e(e+1)/2 linearly related messages (messages of the form (aim + bi), where the ai and bi are known) en-
ables an eavesdropper to recover the messages provided that the moduli ni satisfy ni > 2(e+1)(e+2)/4(e+1)(e+1). H˚astad also showed that sending three linearly related messages
using the Rabin public-key encryption scheme (Algorithm 8.11) is insecure.
The attack on RSA with small decryption exponent d (§8.2.2(iv)) is due to Wiener [1240]. Wiener showed that his attack can be avoided if the encryption exponent e is chosen to be at least 50% longer than the modulus n. In this case, d should be at least 160 bits in length to avoid the square-root discrete logarithm algorithms such as Pollard’s rho algorithm (Algorithm 3.60) and the parallelized variant of van Oorschot and Wiener [1207].
The adaptive chosen-ciphertext attack on RSA encryption (§8.2.2(v)) is due to Davida [302]. See also the related discussion in Denning [327]. Desmedt and Odlyzko [341] described an indifferent chosen-ciphertext attack in which the adversary has to obtain the plaintext corresponding to about Ln[12, 12]carefully chosen-ciphertext, subsequent to which it can decrypt all further ciphertext in Ln[12, 12] time without having to use the authorized user’s decryption machine.
The common modulus attacks on RSA (§8.2.2(vi)) are due to DeLaurentis [320] and Simmons [1137].
The cycling attack (§8.2.2(vii)) was proposed by Simmons and Norris [1151]. Shortly after, Rivest [1052] showed that the cycling attack is extremely unlikely to succeed if the primes p and q are chosen so that: (i) p − 1 and q − 1 have large prime factors p and q , respectively; and (ii) p − 1 and q − 1 have large prime factors p and q , respectively. Maurer [818] showed that condition (ii) is unnecessary. Williams and Schmid [1249] proposed the generalized cycling attack and showed that this attack is really a factoring algorithm. Rivest [1051] provided heuristic evidence that if the primes p and q are selected at random, each having the same bitlength, then the expected time before the generalized cycling attack succeeds is at least p1/3.
The note on message concealing (§8.2.2(viii)) is due to Blakley and Borosh [150], who also extended this work to all composite integers n and determined the number of deranging exponents for a fixed n, i.e., exponents e for which the number of unconcealed messages is the minimum possible. For further work see Smith and Palmer [1158].
Suppose that two or more plaintext messages which have a (known) polynomial relationship (e.g. m1 and m2 might be linearly related: m1 = am2 + b) are encrypted with the same small encryption exponent (e.g. e = 3 or e = 216 + 1). Coppersmith et al. [277] presented a new class of attacks on RSA which enable a passive adversary to recover such plaintext from the corresponding ciphertext. This attack is of practical significance because various cryptographic protocols have been proposed which require the encryption of polynomially related messages. Examples include the key distribution protocol of Tatebayashi, Matsuzaki, and Newman [1188], and the verifiable signature scheme of Franklin and Reiter [421]. Note that these attacks are different from those of §8.2.2(ii) and §8.2.2(vi) where the same plaintext is encrypted under different public keys.
Coppersmith [274] presented an efficient algorithm for finding a root of a polynomial of degree k over Zn, where n is an RSA-like modulus, provided that there there is a root smaller
314 |
Ch. 8 Public-Key Encryption |
than n1/k. The algorithm yielded the following two attacks on RSA with small encryption exponents. If e = 3and if an adversary knows a ciphertext cand more than 2/3of the plaintext mcorresponding to c, then the adversary can efficiently recover the rest of m. Suppose now that messages are padded with random bitstrings and encrypted with exponent e = 3. If an adversary knows two ciphertexts c1 and c2 which correspond to two encryptions of the same message m (with different padding), then the adversary can efficiently recovery m, provided that the padding is less than 1/9 of the length of n. The latter attack suggests that caution must be exercised when using random padding in conjunction with a small encryption exponent.
Let n = pq be a k-bit RSA modulus, where p and q are k/2-bit primes. Coppersmith [273] showed how ncan be factored in polynomial time if the high order k/4bits of pare known. This improves an algorithm of Rivest and Shamir [1058], which requires knowledge of the high order k/3bits of p. For related theoretical work, see Maurer [814]. One implication of Coppersmith’s result is that the method of Vanstone and Zuccherato [1214] for generating RSA moduli having a predetermined set of bits is insecure.
A trapdoor in the RSA cryptosystem was proposed by Anderson [26] whereby a hardware device generates the RSA modulus n = pq in such a way that the hardware manufacturer can easily factor n, but factoring n remains difficult for all other parties. However, Kaliski [652] subsequently showed how to efficiently detect such trapdoors and, in some cases, to actually factor the modulus.
The arguments and recommendations about the use of strong primes in RSA key generation (Note 8.8) are taken from the detailed article by Rivest [1051].
Shamir [1117] proposed a variant of the RSA encryption scheme called unbalanced RSA, which makes it possible to enhance security by increasing the modulus size (e.g. from 500 bits to 5000 bits) without any deterioration in performance. In this variant, the public modulus n is the product of two primes p and q, where one prime (say q) is significantly larger in size than the other; plaintext messages m are in the interval [0,p − 1]. For concreteness, consider the situation where p is a 500-bit prime, and q is a 4500-bit prime. Factoring such a 5000-bit modulus n is well beyond the reach of the special-purpose elliptic curve factoring algorithm of §3.2.4 (whose running time depends on the size of the smallest prime factor of n) and general-purpose factoring algorithms such as the number field sieve of §3.2.7. Shamir recommends that the encryption exponent e be in the interval [20,100], which makes the encryption time with a 5000-bit modulus comparable to the decryption time with a 500-bit modulus. Decryption of the ciphertext c (= md mod n) is accomplished by computing m1 = cd1 mod p, where d1 = d mod (p − 1). Since 0 ≤ m < p, m1 is in fact equal to m. Decryption in unbalanced RSA thus only involves one exponentiation modulo a 500-bit prime, and takes the same time as decryption in ordinary RSA with a 500-bit modulus. This optimization does not apply to the RSA signature scheme (§11.3.1), since the verifier does not know the factor p of the public modulus n.
A permutation polynomial of Zn is a polynomial f(x) Zn[x] which induces a permutation of Zn upon substitution of the elements of Zn; that is, {f(a)|a Zn} = Zn. In RSA encryption the permutation polynomial xe of Zn is used, where gcd(e,φ) = 1. Muller¨ and Nobauer¨ [910] suggested replacing the polynomial xe by the so-called Dickson polynomials to create a modified RSA encryption scheme called the Dickson scheme. The Dickson scheme was further studied by Muller¨ and Nobauer¨ [909]. Other suitable classes of permutation polynomials were investigated by Lidl and Muller¨ [763]. Smith and Lennon [1161] proposed an analogue of the RSA cryptosystem called LUC which is based on Lucas sequences. Due to the relationships between Dickson polynomials and the Lucas sequences,
§8.8 Notes and further references |
315 |
the LUC cryptosystem is closely related to the Dickson scheme. Bleichenbacher, Bosma, and Lenstra [154] presented a chosen-message attack on the LUC signature scheme, undermining the primary advantage claimed for LUC over RSA. Pinch [976, 977] extended the attacks on RSA with small encryption exponent (§8.2.2(ii)) and small decryption exponent (§8.2.2(iv)) to the LUC system.
An analogue of the RSA cryptosystem which uses special kinds of elliptic curves over Zn, where n is a composite integer, was proposed by Koyama et al. [708]. Demytko [321] presented an analogue where there is very little restriction on the types of elliptic curves that can be used. A new cryptosystem based on elliptic curves over Zn in which the message is held in the exponent instead of the group element was proposed by Vanstone and Zuccherato [1213]. The security of all these schemes is based on the difficulty of factoring n. Kurosawa, Okada, and Tsujii [721] showed that the encryption schemes of Koyama et al. and Demytko are vulnerable to low exponent attacks (cf. §8.2.2(ii)); Pinch [977] demonstrated that the attack on RSA with small decryption exponent d (§8.2.2(iv)) also extends to these schemes. Kaliski [649] presented a chosen-ciphertext attack on the Demytko encryption scheme (and also a chosen-message attack on the corresponding signature scheme), and concluded that the present benefits of elliptic curve cryptosystems based on a composite modulus do not seem significant.
§8.3
The Rabin public-key encryption scheme (Algorithm 8.11) was proposed in 1979 by Rabin [1023]. In Rabin’s paper, the encryption function was defined to be E(m) = m(m + b) mod n, where b and n comprise the public key. The security of this scheme is equivalent to the security of the scheme described in Algorithm 8.11 with encryption function E(m) = m2 mod n. A related digital signature scheme is described in §11.3.4. Schwenk and Eisfeld [1104] consider public-key encryption and signature schemes whose security relies on the intractability of factoring polynomials over Zn.
Williams [1246] presented a public-key encryption scheme similar in spirit to Rabin’s but using composite integers n = pq with primes p ≡ 3 (mod 8) and q ≡ 7 (mod 8). Williams’ scheme also has the property that breaking it (that is, recovering plaintext from some given ciphertext) is equivalent to factoring n, but has the advantage over Rabin’s scheme that there is an easy procedure for identifying the intended message from the four roots of a quadratic polynomial. The restrictions on the forms of the primes pand q were removed later by Williams [1248]. A simpler and more efficient scheme also having the properties of provable security and unique decryption was presented by Kurosawa, Ito, and Takeuchi [720]. As with Rabin, all these schemes are vulnerable to a chosen-ciphertext attack (but see Note 8.14).
It is not the case that all public-key encryption schemes for which the decryption problem is provably as difficult as recovering the private key from the public key must succumb to a chosen-ciphertext attack. Goldwasser, Micali, and Rivest [484] were the first to observe this, and presented a digital signature scheme provably secure against an adaptive chosenciphertext attack (see §11.6.4). Naor and Yung [921] proposed the first concrete public-key encryption scheme that is semantically secure against indifferent chosen-ciphertext attack. The Naor-Yung scheme uses two independent keys of a probabilistic public-encryption scheme that is secure against a passive adversary (for example, the Goldwasser-Micali scheme of Algorithm 8.51) to encrypt the plaintext, and then both encryptions are sent along with a non-interactive zero-knowledge proof that the same message was encrypted with both keys. Following this work, Rackoff and Simon [1029] gave the first concrete construction for a public-key encryption scheme that is semantically secure against an adaptive chosen-
316 |
Ch. 8 Public-Key Encryption |
ciphertext attack. Unfortunately, these schemes are all impractical because of the degree of message expansion.
Damg˚ard [297] proposed simple and efficient methods for making public-key encryption schemes secure against indifferent chosen-ciphertext attacks. Zheng and Seberry [1269] noted that Damg˚ard’s schemes are insecure against an adaptive chosen-ciphertext attack, and proposed three practical schemes intended to resist such an attack. The Damg˚ard and Zheng-Seberry schemes were not proven to achieve their claimed levels of security. Bellare and Rogaway [93] later proved that one of the Zheng-Seberry schemes is provably secure against adaptive chosen-ciphertext attacks for their random oracle model. Lim and Lee [766] proposed another method for making public-key schemes secure against adaptive chosen-ciphertext attacks; this scheme was broken by Frankel and Yung [419].
§8.4
The ElGamal cryptosystem was invented by ElGamal [368]. Haber and Lenstra (see Rueppel et al. [1083]) raised the possibility of a trapdoor in discrete logarithm cryptosystems whereby a modulus p is generated (e.g., by a hardware manufacturer) that is intentionally “weak”; cf. Note 4.58. Here, a “weak” prime pis one for which the discrete logarithm problem in Zp is relatively easy. For example, p − 1 may contain only small prime factors, in which case the Pohlig-Hellman algorithm (§3.6.4) would be especially effective. Another example is a prime p for which the number field sieve for discrete logarithms (page 128) is especially well-suited. However, Gordon [509] subsequently showed how such trapdoors can be easily detected. Gordon also showed that the probability of a randomly chosen prime possessing such a trapdoor is negligibly small.
Rivest and Sherman [1061] gave an overview and unified framework for randomized encryption, including comments on chosen-plaintext and chosen-ciphertext attacks.
Elliptic curves were first proposed for use in public-key cryptography by Koblitz [695] and Miller [878]. Recent work on the security and implementation of elliptic curve systems is reported by Menezes [840]. Menezes, Okamoto, and Vanstone [843] showed that if the elliptic curve belongs to a special family called supersingular curves, then the discrete logarithm problem in the elliptic curve group can be reduced in expected polynomial time to the discrete logarithm problem in a small extension of the underlying finite field. Hence, if a supersingular elliptic curve is desired in practice, then it should be carefully chosen.
A modification of ElGamal encryption employing the group of units Zn, where n is a composite integer, was proposed by McCurley [825]; the scheme has the property that breaking it is provably at least as difficult as factoring the modulus n(cf. Fact 3.80). If a cryptanalyst somehow learns the factors of n, then in order to recover plaintext from ciphertext it is still left with the task of solving the Diffie-Hellman problem (§3.7) modulo the factors of n.
Hyperelliptic curve cryptosystems were proposed by Koblitz [696] but little research has since been done regarding their security and practicality.
The possibility of using the class group of an imaginary quadratic number field in publickey cryptography was suggested by Buchmann and Williams [218], however, the attractiveness of this choice was greatly diminished after the invention of a subexponential-time algorithm for computing discrete logarithms in these groups by McCurley [826].
Smith and Skinner [1162] proposed analogues of the Diffie-Hellman key exchange (called LUCDIF) and ElGamal encryption and digital signature schemes (called LUCELG) which use Lucas sequences modulo a prime p instead of modular exponentiation. Shortly thereafter, Laih, Tu, and Tai [733] and Bleichenbacher, Bosma, and Lenstra [154] showed that the analogue of the discrete logarithm problem for Lucas functions polytime reduces to the
§8.8 Notes and further references |
317 |
discrete logarithm problem in the multiplicative group of the finite field Fp2. Since there are subexponential-time algorithms known for the discrete logarithm problem in these fields (cf. §3.6), LUCDIF and LUCELG appear not to offer any advantages over the original schemes.
§8.5
The McEliece encryption scheme (Algorithm 8.30) was introduced in 1978 by McEliece [828]. For information on Goppa codes and their decoding algorithms, see MacWilliams and Sloane [778]. The problem of decoding an arbitrary linear code was shown to be NP- hard by Berlekamp, McEliece, and van Tilborg [120]. The security of the McEliece scheme has been studied by Adams and Meijer [6], Lee and Brickell [742], van Tilburg [1212], Gibson [451], and by Chabaud [235]. Gibson showed that there are, in fact, many trapdoors to a given McEliece encryption transformation, any of which may be used for decryption; this is contrary to the results of Adams and Meijer. However, Gibson notes that there are probably sufficiently few trapdoors that finding one by brute force is computationally infeasible. The cryptanalytic attack reported by Korzhik and Turkin [707] has not been published in its entirety, and is not believed to be an effective attack.
The strength of the McEliece encryption scheme can be severely weakened if the Goppa code is replaced with another type of error-correcting code. For example, Gabidulin, Paramonov, and Tretjakov [435] proposed a modification which uses maximum-rank-distance (MRD) codes in place of Goppa codes. This scheme, and a modification of it by Gabidulin [434], were subsequently shown to be insecure by Gibson [452, 453].
§8.6
The basic and multiple-iterated Merkle-Hellman knapsack encryption schemes (§8.6.1) were introduced by Merkle and Hellman [857]. An elementary overview of knapsack systems is given by Odlyzko [941].
The first polynomial-time attack on the basic Merkle-Hellman scheme (cf. Note 8.40(i)) was devised by Shamir [1114] in 1982. The attack makes use of H. Lenstra’s algorithm for integer programming which runs in polynomial time when the number of variables is fixed, but is inefficient in practice. Lagarias [723] improved the practicality of the attack by reducing the main portion of the procedure to a problem of finding an unusually good simultaneous diophantine approximation; the latter can be solved by the more efficient L3-lattice basis reduction algorithm (§3.10.1). The first attack on the multiple-iterated Merkle-Hellman scheme was by Brickell [200]. For surveys of the cryptanalysis of knapsack schemes, see Brickell [201] and Brickell and Odlyzko [209]. Orton [960] proposed a modification to the multiple-iterated Merkle-Hellman scheme that permits a knapsack density approaching 1, thus avoiding currently known attacks. The high density also allows for a fast digital signature scheme.
Shamir [1109] proposed a fast signature scheme based on the knapsack problem, later broken by Odlyzko [939] using the L3-lattice basis reduction algorithm.
The Merkle-Hellman knapsack scheme illustrates the limitations of using an NP-complete problem to design a secure public-key encryption scheme. Firstly, Brassard [190] showed that under reasonable assumptions, the problem faced by the cryptanalyst cannot be NP- hard unless NP=co-NP, which would be a very surprising result in computational complexity theory. Secondly, complexity theory is concerned primarily with asymptotic complexity of a problem. By contrast, in practice one works with a problem instance of a fixed size. Thirdly, NP-completeness is a measure of the worst-case complexity of a problem. By contrast, cryptographic security should depend on the average-case complexity of the problem (or even better, the problem should be intractable for essentially all instances), since the
318 |
Ch. 8 Public-Key Encryption |
cryptanalyst’s task should be hard for virtually all instances and not merely in the worst case. There are many NP-complete problems that are known to have polynomial-time averagecase algorithms, for example, the graph coloring problem; see Wilf [1243]. Another interesting example is provided by Even and Yacobi [379] who describe a symmetric-key encryption scheme based on the subset sum problem for which breaking the scheme (under a chosen-plaintext attack) is an NP-hard problem, yet an algorithm exists which solves most instances in polynomial time.
The Chor-Rivest knapsack scheme (Algorithm 8.42) was proposed by Chor and Rivest [261]. Recently, Schnorr and Horner¨ [1100] introduced new algorithms for lattice basis reduction that are improvements on the L3-lattice basis reduction algorithm (Algorithm 3.101), and used these to break the Chor-Rivest scheme with parameters {p = 103,h = 12}. Since the density of such knapsack sets is 1.271, the attack demonstrated that subset sum problems with density greater than 1 can be solved via lattice basis reduction. Schnorr and Horner¨ also reported some success solving Chor-Rivest subset sum problems with parameters {p = 151,h = 16}. It remains to be seen whether the techniques of Schnorr and Horner¨ can be successfully applied to the recommended parameter case {p = 197,h = 24}.
Depending on the choice of parameters, the computation of discrete logarithms in the ChorRivest key generation stage (step 4 of Algorithm 8.41) may be a formidable task. A modified version of the scheme which does not require the computation of discrete logarithms in a field was proposed by H. Lenstra [758]. This modified scheme is called the powerline system and is not a knapsack system. It was proven to be at least as secure as the original Chor-Rivest scheme, and is comparable in terms of encryption and decryption speeds.
Qu and Vanstone [1013] showed how the Merkle-Hellman knapsack schemes can be viewed as special cases of certain knapsack-like encryption schemes arising from subset factorizations of finite groups. They also proposed an efficient public-key encryption scheme based on subset factorizations of the additive group Zn of integers modulo n. Blackburn, Murphy, and Stern [143] showed that a simplified variant which uses subset factorizations of the n-dimensional vector space Zn2 over Z2 is insecure.
§8.7
The notion of probabilistic public-key encryption was conceived by Goldwasser and Micali [479], who also introduced the notions of polynomial and semantic security. The equivalence of these two notions (Fact 8.49) was proven by Goldwasser and Micali [479] and Micali, Rackoff, and Sloan [865]. Polynomial security was also studied by Yao [1258], who referred to it as polynomial-time indistinguishability.
The Goldwasser-Micali scheme (Algorithm 8.51) can be described in a general setting by using the notion of a trapdoor predicate. Briefly, a trapdoor predicate is a Boolean function B : {0,1} −→ {0,1} such that given a bit v it is easy to choose an x at random satisfying B(x) = v. Moreover, given a bitstring x, computing B(x) correctly with probability significantly greater than 12 is difficult; however, if certain trapdoor information is known, then it is easy to compute B(x). If entity A’s public key is a trapdoor predicate B, then any other entity encrypts a message bit mi by randomly selecting an xi such that B(xi) = mi, and then sends xi to A. Since Aknows the trapdoor information, she can compute B(xi)to recover mi, but an adversary can do no better than guess the value of mi. Goldwasser and Micali [479] proved that if trapdoor predicates exist, then this probabilistic encryption scheme is polynomially secure. Goldreich and Levin [471] simplified the work of Yao [1258], and showed how any trapdoor length-preserving permutation f can be used to obtain a trapdoor predicate, which in turn can be used to construct a probabilistic public-key encryption
§8.8 Notes and further references |
319 |
scheme.
The Blum-Goldwasser scheme (Algorithm 8.56) was proposed by Blum and Goldwasser [164]. The version given here follows the presentation of Brassard [192]. Two probabilistic public-key encryption schemes, one whose breaking is equivalent to solving the RSA problem (§3.3), and the other whose breaking is equivalent to factoring integers, were proposed by Alexi et al. [23]. The scheme based on RSA is as follows. Let h = lglgn , where (n,e) is entity A’s RSA public key. To encrypt an h-bit message m for A, choose a random y Zn such that the h least significant bits of y equal m, and compute the ciphertext c = ye mod n. A can recover m by computing y = cd mod n, and extracting the h least significant bits of y. While both the schemes proposed by Alexi et al. are more efficient than the Goldwasser-Micali scheme, they suffer from large message expansion and are consequently not as efficient as the Blum-Goldwasser scheme.
The idea of non-malleable cryptography (Definition 8.60) was introduced by Dolev, Dwork, and Naor [357], who also observed Fact 8.61. The paper gives the example of two contract bidders who encrypt their bids. It should not be possible for one bidder A to see the encrypted bid of the other bidder B and somehow be able to offer a bid that was slightly lower, even if A may not know what the resulting bid actually is at that time. Bellare and Rogaway [95] introduced the notion of plaintext-aware encryption (Definition 8.62). They presented the scheme described in Note 8.63, building upon earlier work of Johnson et al. [639]. Rigorous definitions and security proofs were provided, as well as a concrete instantiation of the plaintext-aware encryption scheme using RSA as the trapdoor permutation, and constructing the random functions Gand H from the SHA-1 hash function (§9.4.2(iii)). Johnson and Matyas [640] presented some enhancements to the plaintext-aware encryption scheme. Bellare and Rogaway [93] presented various techniques for deriving appropriate random functions from standard cryptographic hash functions.

Chapter 9
Hash Functions and Data Integrity
Contents in Brief |
|
|
9.1 |
Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
321 |
9.2 |
Classification and framework . . . . . . . . . . . . . . . . . . . . |
322 |
9.3 |
Basic constructions and general results . . . . . . . . . . . . . . . |
332 |
9.4 |
Unkeyed hash functions (MDCs) . . . . . . . . . . . . . . . . . . |
338 |
9.5 |
Keyed hash functions (MACs) . . . . . . . . . . . . . . . . . . . |
352 |
9.6 |
Data integrity and message authentication . . . . . . . . . . . . . |
359 |
9.7 |
Advanced attacks on hash functions . . . . . . . . . . . . . . . . |
368 |
9.8 |
Notes and further references . . . . . . . . . . . . . . . . . . . . |
376 |
9.1 Introduction
Cryptographic hash functions play a fundamental role in modern cryptography. While related to conventional hash functions commonly used in non-cryptographic computer applications – in both cases, larger domains are mapped to smaller ranges – they differ in several important aspects. Our focus is restricted to cryptographic hash functions (hereafter, simply hash functions), and in particular to their use for data integrity and message authentication.
Hash functions take a message as input and produce an output referred to as a hashcode, hash-result, hash-value, or simply hash. More precisely, a hash function h maps bitstrings of arbitrary finite length to strings of fixed length, say n bits. For a domain D and range R with h : D→R and |D| > |R|, the function is many-to-one, implying that the existence of collisions (pairs of inputs with identical output) is unavoidable. Indeed, restricting h to a domain of t-bit inputs (t > n), if h were “random” in the sense that all outputs were essentially equiprobable, then about 2t−n inputs would map to each output, and two randomly chosen inputs would yield the same output with probability 2−n (independent of t). The basic idea of cryptographic hash functions is that a hash-value serves as a compact representative image (sometimes called an imprint, digital fingerprint, or message digest) of an input string, and can be used as if it were uniquely identifiable with that string.
Hash functions are used for data integrity in conjunction with digital signature schemes, where for several reasons a message is typically hashed first, and then the hash-value, as a representative of the message, is signed in place of the original message (see Chapter 11). A distinct class of hash functions, called message authentication codes (MACs), allows message authentication by symmetric techniques. MAC algorithms may be viewed as hash functions which take two functionally distinct inputs, a message and a secret key, and produce a fixed-size (say n-bit) output, with the design intent that it be infeasible in
321

322 |
Ch. 9 Hash Functions and Data Integrity |
practice to produce the same output without knowledge of the key. MACs can be used to provide data integrity and symmetric data origin authentication, as well as identification in symmetric-key schemes (see Chapter 10).
A typical usage of (unkeyed) hash functions for data integrity is as follows. The hashvalue corresponding to a particular message x is computed at time T1. The integrity of this hash-value (but not the message itself) is protected in some manner. At a subsequent time T2, the following test is carried out to determine whether the message has been altered, i.e., whether a message x is the same as the original message. The hash-value of x is computed and compared to the protected hash-value; if they are equal, one accepts that the inputs are also equal, and thus that the message has not been altered. The problem of preserving the integrity of a potentially large message is thus reduced to that of a small fixed-size hashvalue. Since the existence of collisions is guaranteed in many-to-one mappings, the unique association between inputs and hash-values can, at best, be in the computational sense. A hash-value should be uniquely identifiable with a single input in practice, and collisions should be computationally difficult to find (essentially never occurring in practice).
Chapter outline
The remainder of this chapter is organized as follows. §9.2 provides a framework including standard definitions, a discussion of the desirable properties of hash functions and MACs, and consideration of one-way functions. §9.3 presents a general model for iterated hash functions, some general construction techniques, and a discussion of security objectives and basic attacks (i.e., strategies an adversary may pursue to defeat the objectives of a hash function). §9.4 considers hash functions based on block ciphers, and a family of functions based on the MD4 algorithm. §9.5 considers MACs, including those based on block ciphers and customized MACs. §9.6 examines various methods of using hash functions to provide data integrity. §9.7 presents advanced attack methods. §9.8 provides chapter notes with references.
9.2 Classification and framework
9.2.1 General classification
At the highest level, hash functions may be split into two classes: unkeyed hash functions, whose specification dictates a single input parameter (a message); and keyed hash functions, whose specification dictates two distinct inputs, a message and a secret key. To facilitate discussion, a hash function is informally defined as follows.
9.1Definition A hash function (in the unrestricted sense) is a function h which has, as a minimum, the following two properties:
1.compression — h maps an input x of arbitrary finite bitlength, to an output h(x) of fixed bitlength n.
2.ease of computation — given h and an input x, h(x) is easy to compute.

§9.2 Classification and framework |
323 |
As defined here, hash function implies an unkeyed hash function. On occasion when discussion is at a generic level, this term is abused somewhat to mean both unkeyed and keyed hash functions; hopefully ambiguity is limited by context.
For actual use, a more goal-oriented classification of hash functions (beyond keyed vs. unkeyed) is necessary, based on further properties they provide and reflecting requirements of specific applications. Of the numerous categories in such a functional classification, two types of hash functions are considered in detail in this chapter:
1.modification detection codes (MDCs)
Also known as manipulation detection codes, and less commonly as message integrity codes (MICs), the purpose of an MDC is (informally) to provide a representative image or hash of a message, satisfying additional properties as refined below. The end goal is to facilitate, in conjunction with additional mechanisms (see §9.6.4), data integrity assurances as required by specific applications. MDCs are a subclass of unkeyed hash functions, and themselves may be further classified; the specific classes of MDCs of primary focus in this chapter are (cf. Definitions 9.3 and 9.4):
(i)one-way hash functions (OWHFs): for these, finding an input which hashes to a pre-specified hash-value is difficult;
(ii)collision resistant hash functions (CRHFs): for these, finding any two inputs having the same hash-value is difficult.
2.message authentication codes (MACs)
The purpose of a MAC is (informally) to facilitate, without the use of any additional mechanisms, assurances regarding both the source of a message and its integrity (see §9.6.3). MACs have two functionally distinct parameters, a message input and a secret key; they are a subclass of keyed hash functions (cf. Definition 9.7).
Figure 9.1 illustrates this simplified classification. Additional applications of unkeyed hash functions are noted in §9.2.6. Additional applications of keyed hash functions include use in challenge-response identification protocols for computing responses which are a function of both a secret key and a challenge message; and for key confirmation (Definition 12.7). Distinction should be made between a MAC algorithm, and the use of an MDC with a secret key included as part of its message input (see §9.5.2).
It is generally assumed that the algorithmic specification of a hash function is public knowledge. Thus in the case of MDCs, given a message as input, anyone may compute the hash-result; and in the case of MACs, given a message as input, anyone with knowledge of the key may compute the hash-result.
9.2.2 Basic properties and definitions
To facilitate further definitions, three potential properties are listed (in addition to ease of computation and compression as per Definition 9.1), for an unkeyed hash function h with inputs x, x and outputs y, y .
1. preimage resistance — for essentially all pre-specified outputs, it is computationally infeasible to find any input which hashes to that output, i.e., to find any preimage x such that h(x ) = y when given any y for which a corresponding input is not known. 1
2.2nd-preimage resistance — it is computationally infeasible to find any second input
which has the same output as any specified input, i.e., given x, to find a 2nd-preimage x =x such that h(x) = h(x ).
1This acknowledges that an adversary may easily precompute outputs for any small set of inputs, and thereby invert the hash function trivially for such outputs (cf. Remark 9.35).
324 |
Ch. 9 Hash Functions and Data Integrity |
hash functions
|
unkeyed |
keyed |
|
|
modification |
other |
other |
message |
|
detection |
authentication |
|||
applications |
applications |
|||
(MDCs) |
(MACs) |
|||
|
|
OWHF CRHF
 preimage resistant
preimage resistant 
2nd  preimage resistant
preimage resistant
collision resistant 
Figure 9.1: Simplified classification of cryptographic hash functions and applications.
3.collision resistance — it is computationally infeasible to find any two distinct inputs x, x which hash to the same output, i.e., such that h(x) = h(x ). (Note that here there is free choice of both inputs.)
Here and elsewhere, the terms “easy” and “computationally infeasible” (or “hard”) are intentionally left without formal definition; it is intended they be interpreted relative to an understood frame of reference. “Easy” might mean polynomial time and space; or more practically, within a certain number of machine operations or time units – perhaps seconds or milliseconds. A more specific definition of “computationally infeasible” might involve super-polynomial effort; require effort far exceeding understood resources; specify a lower bound on the number of operations or memory required in terms of a specified security parameter; or specify the probability that a property is violated be exponentially small. The properties as defined above, however, suffice to allow practical definitions such as Definitions 9.3 and 9.4 below.
9.2Note (alternate terminology) Alternate terms used in the literature are as follows: preimage resistant ≡ one-way (cf. Definition 9.9); 2nd-preimage resistance ≡ weak collision resistance; collision resistance ≡ strong collision resistance.
For context, one motivation for each of the three major properties above is now given. Consider a digital signature scheme wherein the signature is applied to the hash-value h(x) rather than the message x. Here h should be an MDC with 2nd-preimage resistance, otherwise, an adversary C may observe the signature of some party A on h(x), then find an x such that h(x) = h(x ), and claim that A has signed x . If C is able to actually choose the message which A signs, then C need only find a collision pair (x,x ) rather than the harder task of finding a second preimage of x; in this case, collision resistance is also necessary (cf. Remark 9.93). Less obvious is the requirement of preimage resistance for some public-key signature schemes; consider RSA (Chapter 11), where party A has public key
§9.2 Classification and framework |
325 |
(e,n). C may choose a random value y, compute z = ye mod n, and (depending on the particular RSA signature verification process used) claim that y is A’s signature on z. This (existential) forgery may be of concern if C can find a preimage x such that h(x) = z, and for which x is of practical use.
9.3Definition A one-way hash function (OWHF) is a hash function h as per Definition 9.1 (i.e., offering ease of computation and compression) with the following additional properties, as defined above: preimage resistance, 2nd-preimage resistance.
9.4Definition A collision resistant hash function (CRHF) is a hash function h as per Definition 9.1 (i.e., offering ease of computation and compression) with the following additional properties, as defined above: 2nd-preimage resistance, collision resistance (cf. Fact 9.18).
Although in practice a CRHF almost always has the additional property of preimage resistance, for technical reasons (cf. Note 9.20) this property is not mandated in Definition 9.4.
9.5Note (alternate terminology for OWHF, CRHF) Alternate terms used in the literature are as follows: OWHF ≡ weak one-way hash function (but here preimage resistance is often not explicitly considered); CRHF ≡ strong one-way hash function.
9.6Example (hash function properties)
(i)A simple modulo-32 checksum (32-bit sum of all 32-bit words of a data string) is an easily computed function which offers compression, but is not preimage resistant.
(ii)The function g(x) of Example 9.11 is preimage resistant but provides neither compression nor 2nd-preimage resistance.
(iii)Example 9.13 presents a function with preimage resistance and 2nd-preimage resis-
tance (but not compression). |
|
9.7Definition A message authentication code (MAC) algorithm is a family of functions hk parameterized by a secret key k, with the following properties:
1. ease of computation — for a known function hk, given a value k and an input x, hk(x) is easy to compute. This result is called the MAC-value or MAC.
2.compression — hk maps an input x of arbitrary finite bitlength to an output hk(x) of fixed bitlength n.
Furthermore, given a description of the function family h, for every fixed allowable value of k (unknown to an adversary), the following property holds:
3. computation-resistance — given zero or more text-MAC pairs (xi,hk(xi)), it is computationally infeasible to compute any text-MAC pair (x,hk(x)) for any new input x =xi (including possibly for hk(x) = hk(xi) for some i).
If computation-resistance does not hold, a MAC algorithm is subject to MAC forgery. While computation-resistance implies the property of key non-recovery (it must be computationally infeasible to recover k, given one or more text-MAC pairs (xi,hk(xi)) for that k), key non-recovery does not imply computation-resistance (a key need not always actually be recovered to forge new MACs).
9.8Remark (MAC resistance when key known) Definition 9.7 does not dictate whether MACs need be preimageand collision resistant for parties knowing the key k (as Fact 9.21 implies for parties without k).
326 |
Ch. 9 Hash Functions and Data Integrity |
(i) Objectives of adversaries vs. MDCs
The objective of an adversary who wishes to “attack” an MDC is as follows:
(a)to attack a OWHF: given a hash-value y, find a preimage x such that y = h(x); or given one such pair (x,h(x)), find a second preimage x such that h(x ) = h(x).
(b)to attack a CRHF: find any two inputs x, x , such that h(x ) = h(x).
A CRHF must be designed to withstand standard birthday attacks (see Fact 9.33).
(ii) Objectives of adversaries vs. MACs
The corresponding objective of an adversary for a MAC algorithm is as follows:
(c)to attack a MAC: without prior knowledge of a key k, compute a new text-MAC pair (x,hk(x)) for some text x =xi, given one or more pairs (xi,hk(xi)).
Computation-resistance here should hold whether the texts xi for which matching MACs are available are given to the adversary, or may be freely chosen by the adversary. Similar to the situation for signature schemes, the following attack scenarios thus exist for MACs, for adversaries with increasing advantages:
1.known-text attack. One or more text-MAC pairs (xi,hk(xi)) are available.
2.chosen-text attack. One or more text-MAC pairs (xi,hk(xi)) are available for xi chosen by the adversary.
3.adaptive chosen-text attack. The xi may be chosen by the adversary as above, now allowing successive choices to be based on the results of prior queries.
As a certificational checkpoint, MACs should withstand adaptive chosen-text attack regardless of whether such an attack may actually be mounted in a particular environment. Some practical applications may limit the number of interactions allowed over a fixed period of time, or may be designed so as to compute MACs only for inputs created within the application itself; others may allow access to an unlimited number of text-MAC pairs, or allow MAC verification of an unlimited number of messages and accept any with a correct MAC for further processing.
(iii) Types of forgery (selective, existential)
When MAC forgery is possible (implying the MAC algorithm has been technically defeated), the severity of the practical consequences may differ depending on the degree of control an adversary has over the value x for which a MAC may be forged. This degree is differentiated by the following classification of forgeries:
1.selective forgery – attacks whereby an adversary is able to produce a new text-MAC pair for a text of his choice (or perhaps partially under his control). Note that here the selected value is the text for which a MAC is forged, whereas in a chosen-text attack the chosen value is the text of a text-MAC pair used for analytical purposes (e.g., to forge a MAC on a distinct text).
2.existential forgery – attacks whereby an adversary is able to produce a new text-MAC pair, but with no control over the value of that text.
Key recovery of the MAC key itself is the most damaging attack, and trivially allows selective forgery. MAC forgery allows an adversary to have a forged text accepted as authentic. The consequences may be severe even in the existential case. A classic example is the replacement of a monetary amount known to be small by a number randomly distributed between 0 and 232 − 1. For this reason, messages whose integrity or authenticity is to be verified are often constrained to have pre-determined structure or a high degree of verifiable redundancy, in an attempt to preclude meaningful attacks.

§9.2 Classification and framework |
327 |
Analogously to MACs, attacks on MDC schemes (primarily 2nd-preimage and collision attacks) may be classified as selective or existential. If the message can be partially controlled, then the attack may be classified as partially selective (e.g., see §9.7.1(iii)).
9.2.3 Hash properties required for specific applications
Because there may be costs associated with specific properties – e.g., CRHFs are in general harder to construct than OWHFs and have hash-values roughly twice the bitlength – it should be understood which properties are actually required for particular applications, and why. Selected techniques whereby hash functions are used for data integrity, and the corresponding properties required thereof by these applications, are summarized in Table 9.1.
In general, an MDC should be a CRHF if an untrusted party has control over the exact content of hash function inputs (see Remark 9.93); a OWHF suffices otherwise, including the case where there is only a single party involved (e.g., a store-and-retrieve application). Control over precise format of inputs may be eliminated by introducing into the message randomization that is uncontrollable by one or both parties. Note, however, that data integrity techniques based on a shared secret key typically involve mutual trust and do not address non-repudiation; in this case, collision resistance may or may not be a requirement.
Hash properties required → |
Preimage |
2nd- |
Collision |
Details |
Integrity application ↓ |
resistant |
preimage |
resistant |
|
|
|
|
|
|
MDC + asymmetric signature |
yes |
yes |
yes† |
page 324 |
MDC + authentic channel |
|
yes |
yes† |
page 364 |
MDC + symmetric encryption |
|
|
|
page 365 |
hash for one-way password file |
yes |
|
|
page 389 |
MAC (key unknown to attacker) |
yes |
yes |
yes† |
page 326 |
MAC (key known to attacker) |
|
yes‡ |
|
page 325 |
Table 9.1: Resistance properties required for specified data integrity applications.
†Resistance required if attacker is able to mount a chosen message attack.
‡Resistance required in rare case of multi-cast authentication (see page 378).
9.2.4 One-way functions and compression functions
Related to Definition 9.3 of a OWHF is the following, which is unrestrictive with respect to a compression property.
9.9Definition A one-way function (OWF) is a function f such that for each xin the domain of f, it is easy to compute f(x); but for essentially all y in the range of f, it is computationally infeasible to find any x such that y = f(x).
9.10Remark (OWF vs. domain-restricted OWHF) A OWF as defined here differs from a OWHF with domain restricted to fixed-size inputs in that Definition 9.9 does not require 2nd-preimage resistance. Many one-way functions are, in fact, non-compressing, in which case most image elements have unique preimages, and for these 2nd-preimage resistance holds vacuously – making the difference minor (but see Example 9.11).
328 |
Ch. 9 Hash Functions and Data Integrity |
9.11Example (one-way functions and modular squaring) The squaring of integers modulo a prime p, e.g., f(x) = x2 −1 mod p, behaves in many ways like a random mapping. However, f(x) is not a OWF because finding square roots modulo primes is easy ( §3.5.1). On the other hand, g(x) = x2 mod n is a OWF (Definition 9.9) for appropriate randomly chosen primes p and q where n = pq and the factorization of n is unknown, as finding a preimage (i.e., computing a square root mod n) is computationally equivalent to factoring (Fact 3.46)
and thus intractable. Nonetheless, finding a 2nd-preimage, and, therefore, collisions, is trivial (given x, −x yields a collision), and thus g fits neither the definition of a OWHF nor a CRHF with domain restricted to fixed-size inputs.
9.12Remark (candidate one-way functions) There are, in fact, no known instances of functions which are provably one-way (with no assumptions); indeed, despite known hash function constructions which are provably as secure as NP-complete problems, there is no assurance the latter are difficult. All instances of “one-way functions” to date should thus more properly be qualified as “conjectured” or “candidate” one-way functions. (It thus remains possible, although widely believed most unlikely, that one-way functions do not exist.) A proof of existence would establish P =NP, while non-existence would have devastating cryptographic consequences (see page 377), although not directly implying P = NP.
Hash functions are often used in applications (cf. §9.2.6) which require the one-way property, but not compression. It is, therefore, useful to distinguish three classes of functions (based on the relative size of inputs and outputs):
1.(general) hash functions. These are functions as per Definition 9.1, typically with additional one-way properties, which compress arbitrary-length inputs to n-bit outputs.
2.compression functions (fixed-size hash functions). These are functions as per Definition 9.1, typically with additional one-way properties, but with domain restricted
to fixed-size inputs – i.e., compressing m-bit inputs to n-bit outputs, m > n.
3.non-compressing one-way functions. These are fixed-size hash functions as above, except that n = m. These include one-way permutations, and can be more explicitly described as computationally non-invertible functions.
9.13Example (DES-based OWF) A one-way function can be constructed from DES or any block cipher E which behaves essentially as a random function (see Remark 9.14), as follows: f(x) = Ek(x) x, for any fixed known key k. The one-way nature of this construction can be proven under the assumption that E is a random permutation. An intuitive argument follows. For any choice of y, finding any x (and key k) such that Ek(x) x = y is difficult because for any chosen x, Ek(x) will be essentially random (for any key k) and thus so will Ek(x) x; hence, this will equal y with no better than random chance. By
similar reasoning, if one attempts to use decryption and chooses an x, the probability that Ek−1(x y) = x is no better than random chance. Thus f(x) appears to be a OWF. While f(x) is not a OWHF (it handles only fixed-length inputs), it can be extended to yield one
(see Algorithm 9.41). |
|
9.14Remark (block ciphers and random functions) Regarding random functions and their properties, see §2.1.6. If a block cipher behaved as a random function, then encryption and decryption would be equivalent to looking up values in a large table of random numbers; for a fixed input, the mapping from a key to an output would behave as a random mapping. However, block ciphers such as DES are bijections, and thus at best exhibit behavior more like random permutations than random functions.

§9.2 Classification and framework |
329 |
9.15 Example (one-wayness w.r.t. two inputs) Consider f(x,k) = Ek(x), where E represents DES. This is not a one-way function of the joint input (x,k), because given any func-
tion value y = f(x,k), one can choose any key k and compute x = E−1 |
(y) yielding |
k |
|
a preimage (x ,k ). Similarly, f(x,k) is not a one-way function of x if k is known, as |
|
given y = f(x,k) and k, decryption of y using k yields x. (However, a “black-box” which computes f(x,k) for fixed, externally-unknown k is a one-way function of x.) In contrast, f(x,k) is a one-way function of k; given y = f(x,k) and x, it is not known how to find a preimage k in less than about 255 operations. (This latter concept is utilized in one-time digital signature schemes – see §11.6.2.)
9.16Example (OWF - multiplication of large primes) For appropriate choices of primes p and q, f(p,q) = pq is a one-way function: given p and q, computing n = pq is easy, but given n, finding p and q, i.e., integer factorization, is difficult. RSA and many other cryptographic
systems rely on this property (see Chapter 3, Chapter 8). Note that contrary to many oneway functions, this function f does not have properties resembling a “random” function.
9.17Example (OWF - exponentiation in finite fields) For most choices of appropriately large
primes p and any element α Zp of sufficiently large multiplicative order (e.g., a generator), f(x) = αx mod p is a one-way function. (For example, p must not be such that all the prime divisors of p − 1 are small, otherwise the discrete log problem is feasible by the Pohlig-Hellman algorithm of §3.6.4.) f(x) is easily computed given α, x, and p using
the square-and-multiply technique (Algorithm 2.143), but for most choices p it is difficult, given (y,p,α), to find an x in the range 0 ≤ x ≤ p − 2 such that αx mod p = y, due to the apparent intractability of the discrete logarithm problem (§3.6). Of course, for specific values of f(x) the function can be inverted trivially. For example, the respective preimages of 1 and −1 are known to be 0 and (p −1)/2, and by computing f(x) for any small set of values for x (e.g., x = 1,2,... ,10), these are also known. However, for essentially all y in the range, the preimage of y is difficult to find.
9.2.5 Relationships between properties
In this section several relationships between the hash function properties stated in the preceding section are examined.
9.18Fact Collision resistance implies 2nd-preimage resistance of hash functions.
Justification. Suppose h has collision resistance. Fix an input xj. If h does not have 2ndpreimage resistance, then it is feasible to find a distinct input xi such that h(xi) = h(xj), in which case (xi,xj) is a pair of distinct inputs hashing to the same output, contradicting collision resistance.
9.19Remark (one-way vs. preimage and 2nd-preimage resistant) While the term “one-way” is generally taken to mean preimage resistant, in the hash function literature it is sometimes also used to imply that a function is 2nd-preimage resistant or computationally noninvertible. (Computationally non-invertible is a more explicit term for preimage resistance when preimages are unique, e.g., for one-way permutations. In the case that two or more preimages exist, a function fails to be computationally non-invertible if any one can be found.) This causes ambiguity as 2nd-preimage resistance does not guarantee preimageresistance (Note 9.20), nor does preimage resistance guarantee 2nd-preimage resistance (Example 9.11); see also Remark 9.10. An attempt is thus made to avoid unqualified use of the term “one-way”.

330 |
Ch. 9 Hash Functions and Data Integrity |
9.20Note (collision resistance does not guarantee preimage resistance) Let g be a hash function which is collision resistant and maps arbitrary-length inputs to n-bit outputs. Consider
the function h defined as (here and elsewhere, |
|| denotes concatenation): |
|||
h(x) = |
1 |
|| |
x, |
if x has bitlength n |
0 |
|| |
g(x), |
otherwise. |
|
Then h is an (n + 1)-bit hash function which is collision resistant but not preimage resistant. As a simpler example, the identity function on fixed-length inputs is collision and 2ndpreimage resistant (preimages are unique) but not preimage resistant. While such pathological examples illustrate that collision resistance does not guarantee the difficulty of finding preimages of specific (or even most) hash outputs, for most CRHFs arising in practice it nonetheless appears reasonable to assume that collision resistance does indeed imply preimage resistance.
9.21Fact (implications of MAC properties) Let hk be a keyed hash function which is a MAC algorithm per Definition 9.7 (and thus has the property of computation-resistance). Then hk is, against chosen-text attack by an adversary without knowledge of the key k, (i) both 2nd-preimage resistant and collision resistant; and (ii) preimage resistant (with respect to the hash-input).
Justification. For (i), note that computation-resistance implies hash-results should not even be computable by those without secret key k. For (ii), by way of contradiction, assume h were not preimage resistant. Then recovery of the preimage x for a randomly selected hash-output y violates computation-resistance.
9.2.6Other hash function properties and applications
Most unkeyed hash functions commonly found in practice were originally designed for the purpose of providing data integrity (see §9.6), including digital fingerprinting of messages in conjunction with digital signatures (§9.6.4). The majority of these are, in fact, MDCs designed to have preimage, 2nd-preimage, or collision resistance properties. Because oneway functions are a fundamental cryptographic primitive, many of these MDCs, which typically exhibit behavior informally equated with one-wayness and randomness, have been proposed for use in various applications distinct from data integrity, including, as discussed below:
1.confirmation of knowledge
2.key derivation
3.pseudorandom number generation
Hash functions used for confirmation of knowledge facilitate commitment to data values, or demonstrate possession of data, without revealing such data itself (until possibly a later point in time); verification is possible by parties in possession of the data. This resembles the use of MACs where one also essentially demonstrates knowledge of a secret (but with the demonstration bound to a specific message). The property of hash functions required is preimage resistance (see also partial-preimage resistance below). Specific examples include use in password verification using unencrypted password-image files (Chapter 10); symmetric-key digital signatures (Chapter 11); key confirmation in authenticated key establishment protocols (Chapter 12); and document-dating or timestamping by hash-code registration (Chapter 13).
In general, use of hash functions for purposes other than which they were originally designed requires caution, as such applications may require additional properties (see below)
§9.2 Classification and framework |
331 |
these functions were not designed to provide; see Remark 9.22. Unkeyed hash functions having properties associated with one-way functions have nonetheless been proposed for a wide range of applications, including as noted above:
•key derivation – to compute sequences of new keys from prior keys (Chapter 13). A primary example is key derivation in point-of-sale (POS) terminals; here an important requirement is that the compromise of currently active keys must not compromise the security of previous transaction keys. A second example is in the generation of one-time password sequences based on one-way functions (Chapter 10).
•pseudorandom number generation – to generate sequences of numbers which have various properties of randomness. (A pseudorandom number generator can be used to construct a symmetric-key block cipher, among other things.) Due to the difficulty of producing cryptographically strong pseudorandom numbers (see Chapter 5), MDCs should not be used for this purpose unless the randomness requirements are clearly understood, and the MDC is verified to satisfy these.
For the applications immediately above, rather than hash functions, the cryptographic primitive which is needed may be a pseudorandom function (or keyed pseudorandom function).
9.22Remark (use of MDCs) Many MDCs used in practice may appear to satisfy additional requirements beyond those for which they were originally designed. Nonetheless, the use of arbitrary hash functions cannot be recommended for any applications without careful analysis precisely identifying both the critical properties required by the application and those provided by the function in question (cf. §9.5.2).
Additional properties of one-way hash functions
Additional properties of one-way hash functions called for by the above-mentioned applications include the following.
1.non-correlation. Input bits and output bits should not be correlated. Related to this, an avalanche property similar to that of good block ciphers is desirable whereby every input bit affects every output bit. (This rules out hash functions for which preimage resistance fails to imply 2nd-preimage resistance simply due to the function effectively ignoring a subset of input bits.)
2.near-collision resistance. It should be hard to find any two inputs x, x such that h(x) and h(x ) differ in only a small number of bits.
3.partial-preimage resistance or local one-wayness. It should be as difficult to recover
any substring as to recover the entire input. Moreover, even if part of the input is known, it should be difficult to find the remainder (e.g., if t input bits remain unknown, it should take on average 2t−1 hash operations to find these bits.)
Partial preimage resistance is an implicit requirement in some of the proposed applications of §9.5.2. One example where near-collision resistance is necessary is when only half of the output bits of a hash function are used.
Many of these properties can be summarized as requirements that there be neither local nor global statistical weaknesses; the hash function should not be weaker with respect to some parts of its input or output than others, and all bits should be equally hard. Some of these may be called certificational properties – properties which intuitively appear desirable, although they cannot be shown to be directly necessary.

332 |
Ch. 9 Hash Functions and Data Integrity |
9.3 Basic constructions and general results
9.3.1 General model for iterated hash functions
Most unkeyed hash functions h are designed as iterative processes which hash arbitrarylength inputs by processing successive fixed-size blocks of the input, as illustrated in Figure 9.2.
(a) high-level view |
(b) detailed view |
arbitrary length input
iterated |
compression |
function |
fixed length |
output |
optional output transformation
output
original input x
hash function h
|
|
preprocessing |
append padding bits |
||
append length block |
||
formatted |
|
|
input x = x1x2 · · · xt |
|
|
|
iterated processing |
|
|
compression |
|
|
xi |
function f |
|
|
|
Hi−1 |
f |
|
|
|
|
|
Hi |
H0 = IV |
|
Ht |
|
|
g |
|
|
output h(x) = g(Ht) |
|
Figure 9.2: General model for an iterated hash function.
A hash input x of arbitrary finite length is divided into fixed-length r-bit blocks xi. This preprocessing typically involves appending extra bits (padding) as necessary to attain an overall bitlength which is a multiple of the blocklength r, and often includes (for security reasons – e.g., see Algorithm 9.26) a block or partial block indicating the bitlength of the unpadded input. Each block xi then serves as input to an internal fixed-size hash function f, the compression function of h, which computes a new intermediate result of bitlength n for some fixed n, as a function of the previous n-bit intermediate result and the next input block xi. Letting Hi denote the partial result after stage i, the general process for an iterated

§9.3 Basic constructions and general results |
333 |
hash function with input x = x1x2 ...xt can be modeled as follows:
H0 = IV ; |
Hi = f(Hi−1,xi), 1 ≤ i ≤ t; |
h(x) = g(Ht). (9.1) |
Hi−1 serves as the n-bit chaining variable between stage i − 1 and stage i, and H0 is a pre-defined starting value or initializing value (IV). An optional output transformation g (see Figure 9.2) is used in a final step to map the n-bit chaining variable to an m-bit result g(Ht); g is often the identity mapping g(Ht) = Ht.
Particular hash functions are distinguished by the nature of the preprocessing, compression function, and output transformation.
9.3.2 General constructions and extensions
To begin, an example demonstrating an insecure construction is given. Several secure general constructions are then discussed.
9.23Example (insecure trivial extension of OWHF to CRHF) In the case that an iterated OWHF h yielding n-bit hash-values is not collision resistant (e.g., when a 2n/2 birthday collision attack is feasible – see §9.7.1) one might propose constructing from h a CRHF using as output the concatenation of the last two n-bit chaining variables, so that a t-block message has hash-value Ht−1||Ht rather than Ht. This is insecure as the final message block xt can be held fixed along with Ht, reducing the problem to finding a collision on
Ht−1 for h. |
|
Extending compression functions to hash functions
Fact 9.24 states an important relationship between collision resistant compression functions and collision resistant hash functions. Not only can the former be extended to the latter, but this can be done efficiently using Merkle’s meta-method of Algorithm 9.25 (also called the Merkle-Damg˚ard construction). This reduces the problem of finding such a hash function to that of finding such a compression function.
9.24Fact (extending compression functions) Any compression function f which is collision resistant can be extended to a collision resistant hash function h (taking arbitrary length inputs).
9.25Algorithm Merkle’s meta-method for hashing
INPUT: compression function f which is collision resistant. OUTPUT: unkeyed hash function h which is collision resistant.
1.Suppose f maps (n + r)-bit inputs to n-bit outputs (for concreteness, consider n = 128 and r = 512). Construct a hash function h from f, yielding n-bit hash-values, as follows.
2.Break an input x of bitlength b into blocks x1x2 ...xt each of bitlength r, padding out the last block xt with 0-bits if necessary.
3.Define an extra final block xt+1, the length-block, to hold the right-justified binary representation of b (presume that b < 2r).
4.Letting 0j represent the bitstring of j 0’s, define the n-bit hash-value of x to be h(x) = Ht+1 = f(Ht || xt+1) computed from:
H0 = 0n; Hi = f(Hi−1 || xi), 1 ≤ i ≤ t + 1.
334 |
Ch. 9 Hash Functions and Data Integrity |
The proof that the resulting function h is collision resistant follows by a simple argument that a collision for h would imply a collision for f for some stage i. The inclusion of the length-block, which effectively encodes all messages such that no encoded input is the tail end of any other encoded input, is necessary for this reasoning. Adding such a lengthblock is sometimes called Merkle-Damg˚ard strengthening (MD-strengthening), which is now stated separately for future reference.
9.26Algorithm MD-strengthening
Before hashing a message x = x1x2 ...xt (where xi is a block of bitlength r appropriate
for the relevant compression function) of bitlength b, append a final length-block, xt+1, containing the (say) right-justified binary representation of b. (This presumes b < 2r.)
Cascading hash functions
9.27Fact (cascading hash functions) If either h1 or h2 is a collision resistant hash function, then h(x) = h1(x) || h2(x) is a collision resistant hash function.
If both h1 and h2 in Fact 9.27 are n-bit hash functions, then h produces 2n-bit outputs; mapping this back down to an n-bit output by an n-bit collision-resistant hash function (h1 and h2 are candidates) would leave the overall mapping collision-resistant. If h1 and h2 are independent, then finding a collision for h requires finding a collision for both simultaneously (i.e., on the same input), which one could hope would require the product of the efforts to attack them individually. This provides a simple yet powerful way to (almost surely) increase strength using only available components.
9.3.3Formatting and initialization details
9.28Note (data representation) As hash-values depend on exact bitstrings, different data representations (e.g., ASCII vs. EBCDIC) must be converted to a common format before computing hash-values.
(i) Padding and length-blocks
For block-by-block hashing methods, extra bits are usually appended to a hash input string before hashing, to pad it out to a number of bits which make it a multiple of the relevant block size. The padding bits need not be transmitted/stored themselves, provided the sender and recipient agree on a convention.
9.29Algorithm Padding Method 1
INPUT: data x; bitlength n giving blocksize of data input to processing stage. OUTPUT: padded data x , with bitlength a multiple of n.
1.Append to x as few (possibly zero) 0-bits as necessary to obtain a string x whose bitlength is a multiple of n.
9.30Algorithm Padding Method 2
INPUT: data x; bitlength n giving blocksize of data input to processing stage. OUTPUT: padded data x , with bitlength a multiple of n.
1.Append to x a single 1-bit.

§9.3 Basic constructions and general results |
335 |
2.Then append as few (possibly zero) 0-bits as necessary to obtain a string x whose bitlength is a multiple of n.
9.31Remark (ambiguous padding) Padding Method 1 is ambiguous – trailing 0-bits of the original data cannot be distinguished from those added during padding. Such methods are
acceptable if the length of the data (before padding) is known by the recipient by other means. Padding Method 2 is not ambiguous – each padded string x corresponds to a unique unpadded string x. When the bitlength of the original data x is already a multiple of n, Padding Method 2 results in the creation of an extra block.
9.32Remark (appended length blocks) Appending a logical length-block prior to hashing prevents collision and pseudo-collision attacks which find second messages of different length, including trivial collisions for random IVs (Example 9.96), long-message attacks (Fact 9.37), and fixed-point attacks (page 374). This further justifies the use of MDstrengthening (Algorithm 9.26).
Trailing length-blocks and padding are often combined. For Padding Method 2, a length field of pre-specified bitlength w may replace the final w 0-bits padded if padding would otherwise cause w or more redundant such bits. By pre-agreed convention, the length field typically specifies the bitlength of the original message. (If used instead to specify the number of padding bits appended, deletion of leading blocks cannot be detected.)
(ii) IVs
Whether the IV is fixed, is randomly chosen per hash function computation, or is a function of the data input, the same IV must be used to generate and verify a hash-value. If not known a priori by the verifier, it must be transferred along with the message. In the latter case, this generally should be done with guaranteed integrity (to cut down on the degree of freedom afforded to adversaries, in line with the principle that hash functions should be defined with a fixed or a small set of allowable IVs).
9.3.4 Security objectives and basic attacks
As a framework for evaluating the computational security of hash functions, the objectives of both the hash function designer and an adversary should be understood. Based on Definitions 9.3, 9.4, and 9.7, these are summarized in Table 9.2, and discussed below.
Hash type |
Design goal |
Ideal strength |
Adversary’s goal |
|
|
|
|
OWHF |
preimage resistance; |
2n |
produce preimage; |
|
2nd-preimage resistance |
2n |
find 2nd input, same image |
CRHF |
collision resistance |
2n/2 |
produce any collision |
MAC |
key non-recovery; |
2t |
deduce MAC key; |
|
computation resistance |
Pf = max(2−t, 2−n) |
produce new (msg, MAC) |
Table 9.2: Design objectives for n-bit hash functions (t-bit MAC key). Pf denotes the probability of forgery by correctly guessing a MAC.
Given a specific hash function, it is desirable to be able to prove a lower bound on the complexity of attacking it under specified scenarios, with as few or weak a set of assumptions as possible. However, such results are scarce. Typically the best guidance available regarding
336 |
Ch. 9 Hash Functions and Data Integrity |
the security of a particular hash function is the complexity of the (most efficient) applicable known attack, which gives an upper bound on security. An attack of complexity 2t is one which requires approximately 2t operations, each being an appropriate unit of work (e.g., one execution of the compression function or one encryption of an underlying cipher). The storage complexity of an attack (i.e., storage required) should also be considered.
(i) Attacks on the bitsize of an MDC
Given a fixed message x with n-bit hash h(x), a naive method for finding an input colliding with x is to pick a random bitstring x (of bounded bitlength) and check if h(x ) = h(x). The cost may be as little as one compression function evaluation, and memory is negligible. Assuming the hash-code approximates a uniform random variable, the probability of a match is 2−n. The implication of this is Fact 9.33, which also indicates the effort required to find collisions if x may itself be chosen freely. Definition 9.34 is motivated by the design goal that the best possible attack should require no less than such levels of effort, i.e., essentially brute force.
9.33Fact (basic hash attacks) For an n-bit hash function h, one may expect a guessing attack to find a preimage or second preimage within 2n hashing operations. For an adversary able to choose messages, a birthday attack (see §9.7.1) allows colliding pairs of messages x, x with h(x) = h(x ) to be found in about 2n/2 operations, and negligible memory.
9.34Definition An n-bit unkeyed hash function has ideal security if both: (1) given a hash output, producing each of a preimage and a 2nd-preimage requires approximately 2 n operations; and (2) producing a collision requires approximately 2n/2 operations.
(ii) Attacks on the MAC key space
An attempt may be made to determine a MAC key using exhaustive search. With a single known text-MAC pair, an attacker may compute the n-bit MAC on that text under all possible keys, and then check which of the computed MAC-values agrees with that of the known pair. For a t-bit key space this requires 2t MAC operations, after which one expects 1 + 2t−n candidate keys remain. Assuming the MAC behaves as a random mapping, it can be shown that one can expect to reduce this to a unique key by testing the candidate keys using just over t/n text-MAC pairs. Ideally, a MAC key (or information of cryptographically equivalent value) would not be recoverable in fewer than 2t operations.
As a probabilistic attack on the MAC key space distinct from key recovery, note that for a t-bit key and a fixed input, a randomly guessed key will yield a correct ( n-bit) MAC with probability ≈ 2−t for t < n.
(iii) Attacks on the bitsize of a MAC
MAC forgery involves producing any input x and the corresponding correct MAC without having obtained the latter from anyone with knowledge of the key. For an n-bit MAC algorithm, either guessing a MAC for a given input, or guessing a preimage for a given MAC output, has probability of success about 2−n, as for an MDC. A difference here, however, is that guessed MAC-values cannot be verified off-line without known text-MAC pairs – either knowledge of the key, or a “black-box” which provides MACs for given inputs (i.e., a chosen-text scenario) is required. Since recovering the MAC key trivially allows forgery, an attack on the t-bit key space (see above) must be also be considered here. Ideally, an adversary would be unable to produce new (correct) text-MAC pairs (x,y) with probability significantly better than max(2−t,2−n), i.e., the better of guessing a key or a MAC-value.

§9.3 Basic constructions and general results |
337 |
(iv)Attacks using precomputations, multiple targets, and long messages
9.35Remark (precomputation of hash values) For both preimage and second preimage attacks, an opponent who precomputes a large number of hash function input-output pairs may trade
off precomputation plus storage for subsequent attack time. For example, for a 64-bit hash value, if one randomly selects 240 inputs, then computes their hash values and stores (hash value, input) pairs indexed by hash value, this precomputation of O(240) time and space
allows an adversary to increase the probability of finding a preimage (per one subsequent hash function computation) from 2−64 to 2−24. Similarly, the probability of finding a second preimage increases to r times its original value (when no stored pairs are known) if r input-output pairs of a OWHF are precomputed and tabulated.
9.36Remark (effect of parallel targets for OWHFs) In a basic attack, an adversary seeks a sec-
ond preimage for one fixed target (the image computed from a first preimage). If there are r targets and the goal is to find a second preimage for any one of these r, then the probability of success increases to r times the original probability. One implication is that when using hash functions in conjunction with keyed primitives such as digital signatures, repeated use of the keyed primitive may weaken the security of the combined mechanism in the following sense. If r signed messages are available, the probability of a hash collision increases r-fold (cf. Remark 9.35), and colliding messages yield equivalent signatures, which an opponent could not itself compute off-line.
Fact 9.37 reflects a related attack strategy of potential concern when using iterated hash functions on long messages.
9.37Fact (long-message attack for 2nd-preimage) Let h be an iterated n-bit hash function with compression function f (as in equation (9.1), without MD-strengthening). Let x be a message consisting of t blocks. Then a 2nd-preimage for h(x) can be found in time (2n/s) + s operations of f, and in space n(s+lg(s)) bits, for any s in the range 1 ≤ s ≤ min(t,2n/2).
Justification. The idea is to use a birthday attack on the intermediate hash-results; a sketch for the choice s = t follows. Compute h(x), storing (Hi,i) for each of the t intermediate hash-results Hi corresponding to the t input blocks xi in a table such that they may be later indexed by value. Compute h(z) for random choices z, checking for a collision involving h(z) in the table, until one is found; approximately 2n/s values z will be required, by the birthday paradox. Identify the index j from the table responsible for the collision; the input zxj+1xj+2 ...xt then collides with x.
9.38Note (implication of long messages) Fact 9.37 implies that for “long” messages, a 2ndpreimage is generally easier to find than a preimage (the latter takes at most 2n operations), becoming moreso with the length of x. For t ≥ 2n/2, computation is minimized by choosing s = 2n/2 in which case a 2nd-preimage costs about 2n/2 executions of f (comparable to the difficulty of finding a collision).
9.3.5Bitsizes required for practical security
Suppose that a hash function produces n-bit hash-values, and as a representative benchmark assume that 280 (but not fewer) operations is acceptably beyond computational feasibility.2 Then the following statements may be made regarding n.
2Circa 1996, 240 simple operations is quite feasible, and 256 is considered quite reachable by those with sufficient motivation (possibly using parallelization or customized machines).

338 |
Ch. 9 Hash Functions and Data Integrity |
1.For a OWHF, n ≥ 80 is required. Exhaustive off-line attacks require at most 2n operations; this may be reduced with precomputation (Remark 9.35).
2.For a CRHF, n ≥ 160 is required. Birthday attacks are applicable (Fact 9.33).
3.For a MAC, n ≥ 64 along with a MAC key of 64-80 bits is sufficient for most applications and environments (cf. Table 9.1). If a single MAC key remains in use, off-line attacks may be possible given one or more text-MAC pairs; but for a proper MAC algorithm, preimage and 2nd-preimage resistance (as well as collision resistance) should follow directly from lack of knowledge of the key, and thus security with respect to such attacks should depend on the keysize rather than n. For attacks requiring on-line queries, additional controls may be used to limit the number of such queries, constrain the format of MAC inputs, or prevent disclosure of MAC outputs for random (chosen-text) inputs. Given special controls, values as small as n = 32 or
40 may be acceptable; but caution is advised, since even with one-time MAC keys, the chance any randomly guessed MAC being correct is 2−n, and the relevant factors
are the total number of trials a system is subject to over its lifetime, and the consequences of a single successful forgery.
These guidelines may be relaxed somewhat if a lower threshold of computational infeasibility is assumed (e.g., 264 instead of 280). However, an additional consideration to be taken into account is that for both a CRHF and a OWHF, not only can off-line attacks be carried out, but these can typically be parallelized. Key search attacks against MACs may also be parallelized.
9.4 Unkeyed hash functions (MDCs)
A move from general properties and constructions to specific hash functions is now made, and in this section the subclass of unkeyed hash functions known as modification detection codes (MDCs) is considered. From a structural viewpoint, these may be categorized based on the nature of the operations comprising their internal compression functions. From this viewpoint, the three broadest categories of iterated hash functions studied to date are hash functions based on block ciphers, customized hash functions, and hash functions based on modular arithmetic. Customized hash functions are those designed specifically for hashing, with speed in mind and independent of other system subcomponents (e.g., block cipher or modular multiplication subcomponents which may already be present for non-hashing purposes).
Table 9.3 summarizes the conjectured security of a subset of the MDCs subsequently discussed in this section. Similar to the case of block ciphers for encryption (e.g. 8- or 12round DES vs. 16-round DES), security of MDCs often comes at the expense of speed, and tradeoffs are typically made. In the particular case of block-cipher-based MDCs, a provably secure scheme of Merkle (see page 378) with rate 0.276 (see Definition 9.40) is known but little-used, while MDC-2 is widely believed to be (but not provably) secure, has rate = 0.5, and receives much greater attention in practice.
9.4.1 Hash functions based on block ciphers
A practical motivation for constructing hash functions from block ciphers is that if an efficient implementation of a block cipher is already available within a system (either in hardware or software), then using it as the central component for a hash function may provide

§9.4 Unkeyed hash functions (MDCs) |
|
|
|
|
339 |
|||
|
|
|
|
|
|
|
|
|
|
|
↓Hash function |
n |
m |
Preimage |
Collision |
Comments |
|
|
|
|
|
|
|
|
|
|
|
|
Matyas-Meyer-Oseasa |
n |
n |
2n |
2n/2 |
for keylength = n |
|
|
|
MDC-2 (with DES)b |
64 |
128 |
2 · 282 |
2 ·254 |
rate 0.5 |
|
|
|
MDC-4 (with DES) |
64 |
128 |
2109 |
4 ·254 |
rate 0.25 |
|
|
|
Merkle (with DES) |
106 |
128 |
2112 |
256 |
rate 0.276 |
|
|
|
MD4 |
512 |
128 |
2128 |
220 |
Remark 9.50 |
|
|
|
MD5 |
512 |
128 |
2128 |
264 |
Remark 9.52 |
|
|
|
RIPEMD-128 |
512 |
128 |
2128 |
264 |
– |
|
|
|
SHA-1, RIPEMD-160 |
512 |
160 |
2160 |
280 |
– |
|
|
|
|
|
|
|
|
|
|
aThe same strength is conjectured for Davies-Meyer and Miyaguchi-Preneel hash functions. bStrength could be increased using a cipher with keylength equal to cipher blocklength.
Table 9.3: Upper bounds on strength of selected hash functions. n-bit message blocks are processed to produce m-bit hash-values. Number of cipher or compression function operations currently believed necessary to find preimages and collisions are specified, assuming no underlying weaknesses for block ciphers (figures for MDC-2 and MDC-4 account for DES complementation and weak key properties). Regarding rate, see Definition 9.40.
the latter functionality at little additional cost. The (not always well-founded) hope is that a good block cipher may serve as a building block for the creation of a hash function with properties suitable for various applications.
Constructions for hash functions have been given which are “provably secure” assuming certain ideal properties of the underlying block cipher. However, block ciphers do not possess the properties of random functions (for example, they are invertible – see Remark 9.14). Moreover, in practice block ciphers typically exhibit additional regularities or weaknesses (see §9.7.4). For example, for a block cipher E, double encryption using an encrypt-decrypt (E-D) cascade with keys K1, K2 results in the identity mapping when K1 = K2. In summary, while various necessary conditions are known, it is unclear exactly what requirements of a block cipher are sufficient to construct a secure hash function, and properties adequate for a block cipher (e.g., resistance to chosen-text attack) may not guarantee a good hash function.
In the constructions which follow, Definition 9.39 is used.
9.39Definition An (n,r) block cipher is a block cipher defining an invertible function from n-bit plaintexts to n-bit ciphertexts using an r-bit key. If E is such a cipher, then Ek(x) denotes the encryption of x under key k.
Discussion of hash functions constructed from n-bit block ciphers is divided between those producing single-length (n-bit) and double-length (2n-bit) hash-values, where single and double are relative to the size of the block cipher output. Under the assumption that computations of 264 operations are infeasible,3 the objective of single-length hash functions is to provide a OWHF for ciphers of blocklength near n = 64, or to provide CRHFs for cipher blocklengths near n = 128. The motivation for double-length hash functions is that many n-bit block ciphers exist of size approximately n = 64, and single-length hash-codes of this size are not collision resistant. For such ciphers, the goal is to obtain hash-codes of bitlength 2n which are CRHFs.
In the simplest case, the size of the key used in such hash functions is approximately the same as the blocklength of the cipher (i.e., n bits). In other cases, hash functions use
3 |
80 |
|
|
The discussion here is easily altered for a more conservative bound, e.g., 2 |
operations as used in §9.3.5. |
Here 264 is more convenient for discussion, due to the omnipresence of 64-bit block ciphers.
340 |
Ch. 9 Hash Functions and Data Integrity |
larger (e.g., double-length) keys. Another characteristic to be noted in such hash functions is the number of block cipher operations required to produce a hash output of blocklength equal to that of the cipher, motivating the following definition.
9.40Definition Let h be an iterated hash function constructed from a block cipher, with compression function f which performs s block encryptions to process each successive n-bit message block. Then the rate of h is 1/s.
The hash functions discussed in this section are summarized in Table 9.4. The Matyas- Meyer-Oseas and MDC-2 algorithms are the basis, respectively, of the two generic hash functions in ISO standard 10118-2, each allowing use of any n-bit block cipher E and providing hash-codes of bitlength m ≤ n and m ≤ 2n, respectively.
Hash function |
(n,k,m) |
Rate |
|
|
|
Matyas-Meyer-Oseas |
(n,k,n) |
1 |
Davies-Meyer |
(n,k,n) |
k/n |
Miyaguchi-Preneel |
(n,k,n) |
1 |
MDC-2 (with DES) |
(64,56,128) |
1/2 |
MDC-4 (with DES) |
(64,56,128) |
1/4 |
Table 9.4: Summary of selected hash functions based on n-bit block ciphers. k = key bitsize (approximate); function yields m-bit hash-values.
(i) Single-length MDCs of rate 1
The first three schemes described below, and illustrated in Figure 9.3, are closely related single-length hash functions based on block ciphers. These make use of the following predefined components:
1.a generic n-bit block cipher EK parametrized by a symmetric key K;
2.a function g which maps n-bit inputs to keys K suitable for E (if keys for E are also of length n, g might be the identity function); and
3.a fixed (usually n-bit) initial value IV , suitable for use with E.
Matyas-Meyer-Oseas
xi
Hi−1 |
g |
E |
|
Davies-Meyer
Hi−1
xi
 E
E
Miyaguchi-Preneel
xi
Hi−1  g
g 

 E
E
Hi |
Hi |
Hi |
Figure 9.3: Three single-length, rate-one MDCs based on block ciphers.

§9.4 Unkeyed hash functions (MDCs) |
341 |
9.41Algorithm Matyas-Meyer-Oseas hash
INPUT: bitstring x.
OUTPUT: n-bit hash-code of x.
1.Input x is divided into n-bit blocks and padded, if necessary, to complete last block. Denote the padded message consisting of t n-bit blocks: x1x2 ...xt. A constant n- bit initial value IV must be pre-specified.
2.The output is Ht defined by: H0 = IV ; Hi = Eg(Hi−1)(xi) xi, 1 ≤ i ≤ t.
9.42Algorithm Davies-Meyer hash
INPUT: bitstring x.
OUTPUT: n-bit hash-code of x.
1.Input x is divided into k-bit blocks where k is the keysize, and padded, if necessary, to complete last block. Denote the padded message consisting of tk-bit blocks: x1x2
... xt. A constant n-bit initial value IV must be pre-specified.
2.The output is Ht defined by: H0 = IV ; Hi = Exi (Hi−1) Hi−1, 1 ≤ i ≤ t.
9.43Algorithm Miyaguchi-Preneel hash
This scheme is identical to that of Algorithm 9.41, except the output Hi−1 from the previous stage is also XORed to that of the current stage. More precisely, Hi is redefined as: H0 =
IV ; Hi = Eg(Hi−1)(xi) xi Hi−1, 1 ≤ i ≤ t.
9.44Remark (dual schemes) The Davies-Meyer hash may be viewed as the ‘dual’ of the Mat- yas-Meyer-Oseas hash, in the sense that xi and Hi−1 play reversed roles. When DES is used as the block cipher in Davies-Meyer, the input is processed in 56-bit blocks (yielding rate 56/64 < 1), whereas Matyas-Meyer-Oseas and Miyaguchi-Preneel process 64-bit blocks.
9.45Remark (black-box security) Aside from heuristic arguments as given in Example 9.13, it appears that all three of Algorithms 9.41, 9.42, and 9.43 yield hash functions which are
provably secure under an appropriate “black-box” model (e.g., assuming E has the required randomness properties, and that attacks may not make use of any special properties or internal details of E). “Secure” here means that finding preimages and collisions (in fact, pseudo-preimages and pseudo-collisions – see §9.7.2) require on the order of 2n and 2n/2 n-bit block cipher operations, respectively. Due to their single-length nature, none of these three is collision resistant for underlying ciphers of relatively small blocklength (e.g., DES, which yields 64-bit hash-codes).
Several double-length hash functions based on block ciphers are considered next.
(ii) Double-length MDCs: MDC-2 and MDC-4
MDC-2 and MDC-4 are manipulation detection codes requiring 2 and 4, respectively, block cipher operations per block of hash input. They employ a combination of either 2 or 4 iterations of the Matyas-Meyer-Oseas (single-length) scheme to produce a double-length hash. When used as originally specified, using DES as the underlying block cipher, they produce 128-bit hash-codes. The general construction, however, can be used with other block ciphers. MDC-2 and MDC-4 make use of the following pre-specified components:

342 |
Ch. 9 Hash Functions and Data Integrity |
1.DES as the block cipher EK of bitlength n = 64 parameterized by a 56-bit key K;
2.two functions g and g˜ which map 64-bit values U to suitable 56-bit DES keys as follows. For U = u1u2 ...u64, delete every eighth bit starting with u8, and set the 2nd and 3rd bits to ‘10’ for g, and ‘01’ for g˜:
g(U) = u1 1 0 u4u5u6u7u9u10 ...u63. g˜(U) = u1 0 1 u4u5u6u7u9u10 ...u63.
(The resulting values are guaranteed not to be weak or semi-weak DES keys, as all
such keys have bit 2 = bit 3; see page 375. Also, this guarantees the security require-
mentthat g(IV ) =g(IV˜ ).)
MDC-2 is specified in Algorithm 9.46 and illustrated in Figure 9.4.
Xi
|
in1 |
|
|
in2 |
|
in3 |
g |
E |
|
in4 |
|
Hi−1 |
|
E |
g˜ |
Hi−1 |
A |
B |
C |
D |
A |
D |
C |
B |
out1 |
|
|
out2 |
Hi |
|
|
|
|
Hi |
||
Figure 9.4: Compression function of MDC-2 hash function. E = DES.
9.46Algorithm MDC-2 hash function (DES-based)
INPUT: string x of bitlength r = 64t for t ≥ 2. OUTPUT: 128-bit hash-code of x.
1.Partition x into 64-bit blocks xi: x = x1x2 ...xt.
2. Choose the 64-bit non-secret constants , (the same constants must be used for
IV IV
MDC verification) from a set of recommended prescribed values. A default set of
prescribed values is (in hexadecimal): 0x5252525252525252,
IV = IV =
0x2525252525252525.

§9.4 Unkeyed hash functions (MDCs) |
343 |
3. Let || denote concatenation, and CL, CR the left and right 32-bit halves of Ci. The |
||||||||||||
|
|
|
i |
i |
|
|
|
|
|
|
|
|
|
|
H |
defined as follows (for |
|
i |
|
t): |
|
|
|
||
output is h(x) = Ht || t |
|
|
|
1 ≤ |
|
≤ |
L |
|| Ci |
R |
|||
H0 = IV ; |
ki = g(Hi−1); |
Ci = Eki (xi) xi; |
Hi = Ci |
|
||||||||
|
|
|
|
|
|
|
|
|
L |
|
R |
|
H |
IV |
|
C E |
x x |
|
H C |
|
|||||
k g H |
|
|| |
C . |
|||||||||
0 |
= ; |
i = ( |
i−1); |
i = ki |
( |
i) |
i; |
|
i = i |
i |
|
|
In Algorithm 9.46, padding may be necessary to meet the bitlength constraint on the input x. In this case, an unambiguous padding method may be used (see Remark 9.31), possibly including MD-strengthening (see Remark 9.32).
MDC-4 (see Algorithm 9.47 and Figure 9.5) is constructed using the MDC-2 compression function. One iteration of the MDC-4 compression function consists of two sequential executions of the MDC-2 compression function, where:
1.the two 64-bit data inputs to the first MDC-2 compression are both the same next 64-bit message block;
2.the keys for the first MDC-2 compression are derived from the outputs (chaining variables) of the previous MDC-4 compression;
3.the keys for the second MDC-2 compression are derived from the outputs (chaining variables) of the first MDC-2 compression; and
4.the two 64-bit data inputs for the second MDC-2 compression are the outputs (chaining variables) from the opposite sides of the previous MDC-4 compression.
9.47Algorithm MDC-4 hash function (DES-based)
INPUT: string x of bitlength r = 64t for t ≥ 2. (See MDC-2 above regarding padding.) OUTPUT: 128-bit hash-code of x.
1.As in step 1 of MDC-2 above.
2.As in step 2 of MDC-2 above.
1 ≤ i ≤ t): |
|
|
|
( ) = |
G |
t || |
t |
|
|
|
|
|
|
3. With notation as in MDC-2, the output is h x |
|
|
G defined as follows (for |
||||||||||
|
|
|
|
G |
IV |
|
|
|
|
|
|
|
|
|
|
G0 = IV ; |
0 = |
|
; |
|
L |
|
|
R |
|
||
|
|
i |
(xi) xi; |
|
|
Hi = C |
iL |
|| |
R |
|
|||
ki = g(Gi−1); |
Ci = Ek |
|
|
|
Ci |
|
|||||||
ki = g(Gi−1); |
i = Eki (xi) i; |
|
i |
= i L|| |
i |
R |
|||||||
ji = g(Hi); |
|
C |
|
x |
|
|
H |
C |
|
|
C |
|
|
Di = Eji (Gi−1) Gi−1; |
Gi = Di |
|| Di |
|
||||||||||
j g H |
D E |
G |
G |
|
|
G D L |
|| |
D R . |
|||||
i = ( i); |
i |
= ji ( |
i−1) i−1; |
|
i |
= i |
|
i |
|
||||
9.4.2 Customized hash functions based on MD4
Customized hash functions are those which are specifically designed “from scratch” for the explicit purpose of hashing, with optimized performance in mind, and without being constrained to reusing existing system components such as block ciphers or modular arithmetic. Those having received the greatest attention in practice are based on the MD4 hash function.
Number 4 in a series of hash functions (Message Digest algorithms), MD4 was designed specifically for software implementation on 32-bit machines. Security concerns motivated the design of MD5 shortly thereafter, as a more conservative variation of MD4.
344 |
Ch. 9 Hash Functions and Data Integrity |
|
|
Xi |
|
|
|
in1 |
|
in2 |
|
Gi−1 |
in3 |
|
in4 |
Gi−1 |
|
MDC-2 compression function |
|
||
|
out1 Hi |
|
out2 |
|
|
Hi |
|
||
|
Gi−1 Gi−1 |
in2 |
|
|
|
in1 |
|
|
|
|
in3 |
|
in4 |
|
|
MDC-2 compression function |
|
||
|
out1 |
|
out2 |
|
|
Gi |
|
|
|
|
Gi |
|
||
Figure 9.5: Compression function of MDC-4 hash function
Other important subsequent variants include the Secure Hash Algorithm (SHA-1), the hash function RIPEMD, and its strengthened variants RIPEMD-128 and RIPEMD-160. Parameters for these hash functions are summarized in Table 9.5. “Rounds × Steps per round” refers to operations performed on input blocks within the corresponding compression function. Table 9.6 specifies test vectors for a subset of these hash functions.
Notation for description of MD4-family algorithms
Table 9.7 defines the notation for the description of MD4-family algorithms described below. Note 9.48 addresses the implementation issue of converting strings of bytes to words in an unambiguous manner.
9.48Note (little-endian vs. big-endian) For interoperable implementations involving byte-to- word conversions on different processors (e.g., converting between 32-bit words and groups of four 8-bit bytes), an unambiguous convention must be specified. Consider a stream of bytes Bi with increasing memory addresses i, to be interpreted as a 32-bit word with numerical value W. In little-endian architectures, the byte with the lowest memory address (B1) is the least significant byte: W = 224B4 + 216B3 + 28B2 + B1. In big-endian
architectures, the byte with the lowest address (B1) is the most significant byte: W =
224B1 + 216B2 + 28B3 + B4.
(i) MD4
MD4 (Algorithm 9.49) is a 128-bit hash function. The original MD4 design goals were that breaking it should require roughly brute-force effort: finding distinct messages with the same hash-value should take about 264 operations, and finding a message yielding a
§9.4 Unkeyed hash functions (MDCs) |
345 |
Name |
Bitlength |
Rounds × Steps per round |
Relative speed |
|
|
|
|
|
|
MD4 |
128 |
3 |
× 16 |
1.00 |
MD5 |
128 |
4 |
× 16 |
0.68 |
RIPEMD-128 |
128 |
4 |
× 16 twice (in parallel) |
0.39 |
SHA-1 |
160 |
4 |
× 20 |
0.28 |
RIPEMD-160 |
160 |
5 |
× 16 twice (in parallel) |
0.24 |
Table 9.5: Summary of selected hash functions based on MD4.
Name |
String |
Hash value (as a hex byte string) |
|
|
|
|
|
MD4 |
“” |
31d6cfe0d16ae931b73c59d7e0c089c0 |
|
|
“a” |
bde52cb31de33e46245e05fbdbd6fb24 |
|
|
“abc” |
a448017aaf21d8525fc10ae87aa6729d |
|
|
“abcdefghijklmnopqrstuvwxyz” |
d79e1c308aa5bbcdeea8ed63df412da9 |
|
|
|
|
|
MD5 |
“” |
d41d8cd98f00b204e9800998ecf8427e |
|
|
“a” |
0cc175b9c0f1b6a831c399e269772661 |
|
|
“abc” |
900150983cd24fb0d6963f7d28e17f72 |
|
|
“abcdefghijklmnopqrstuvwxyz” |
c3fcd3d76192e4007dfb496cca67e13b |
|
|
|
|
|
SHA-1 |
“” |
da39a3ee5e6b4b0d3255bfef95601890afd80709 |
|
|
“a” |
86f7e437faa5a7fce15d1ddcb9eaeaea377667b8 |
|
|
“abc” |
a9993e364706816aba3e25717850c26c9cd0d89d |
|
|
“abcdefghijklmnopqrstuvwxyz” |
32d10c7b8cf96570ca04ce37f2a19d84240d3a89 |
|
|
|
|
|
RIPEMD-160 |
“” |
9c1185a5c5e9fc54612808977ee8f548b2258d31 |
|
|
“a” |
0bdc9d2d256b3ee9daae347be6f4dc835a467ffe |
|
|
“abc” |
8eb208f7e05d987a9b044a8e98c6b087f15a0bfc |
|
|
“abcdefghijklmnopqrstuvwxyz” |
f71c27109c692c1b56bbdceb5b9d2865b3708dbc |
|
|
|
|
|
|
|
Table 9.6: Test vectors for selected hash functions. |
|||
|
|
|
|
|
|
|
Notation |
Meaning |
|||
|
|
|
|
|
|
|
u, v, w |
variables representing 32-bit quantities |
|||
|
0x67452301 |
hexadecimal 32-bit integer (least significant byte: 01) |
|||
+ |
addition modulo 232 |
||||
|
|
|
bitwise complement |
||
|
u |
||||
|
u ← s |
result of rotating u left through s positions |
|||
|
uv |
bitwise AND |
|||
|
u v |
bitwise inclusive-OR |
|||
|
u v |
bitwise exclusive-OR |
|||
|
f(u,v,w) |
uv |
|
|
|
|
uw |
||||
|
g(u,v,w) |
uv uw vw |
|||
|
h(u,v,w) |
u v w |
|||
|
(X1,... ,Xj) ← |
simultaneous assignments (Xi ← Yi), |
|||
|
(Y1,... ,Yj) |
where (Y1,... ,Yj) is evaluated prior to any assignments |
|||
Table 9.7: Notation for MD4-family algorithms.

346 |
Ch. 9 Hash Functions and Data Integrity |
pre-specified hash-value about 2128 operations. It is now known that MD4 fails to meet this goal (Remark 9.50). Nonetheless, a full description of MD4 is included as Algorithm 9.49 for historical and cryptanalytic reference. It also serves as a convenient reference for describing, and allowing comparisons between, other hash functions in this family.
9.49Algorithm MD4 hash function
INPUT: bitstring x of arbitrary bitlength b ≥ 0. (For notation see Table 9.7.) OUTPUT: 128-bit hash-code of x. (See Table 9.6 for test vectors.)
1.Definition of constants. Define four 32-bit initial chaining values (IVs):
h1 = 0x67452301, h2 = 0xefcdab89, h3 = 0x98badcfe, h4 = 0x10325476. Define additive 32-bit constants:
y[j] = 0, 0 ≤ j ≤ 15;
y[j] = 0x5a827999, 16 ≤ j ≤ 31; (constant = square-root of 2) y[j] = 0x6ed9eba1, 32 ≤ j ≤ 47; (constant = square-root of 3)
Define order for accessing source words (each list contains 0 through 15): z[0..15] = [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15],
z[16..31] = [0,4,8,12,1,5,9,13,2,6,10,14,3,7,11,15], z[32..47] = [0,8,4,12,2,10,6,14,1,9,5,13,3,11,7,15]. Finally define the number of bit positions for left shifts (rotates): s[0..15] = [3,7,11,19,3,7,11,19,3,7,11,19,3,7,11,19], s[16..31] = [3,5,9,13,3,5,9,13,3,5,9,13,3,5,9,13], s[32..47] = [3,9,11,15,3,9,11,15,3,9,11,15,3,9,11,15].
2.Preprocessing. Pad x such that its bitlength is a multiple of 512, as follows. Append a single 1-bit, then append r−1 (≥ 0) 0-bits for the smallest r resulting in a bitlength 64 less than a multiple of 512. Finally append the 64-bit representation of b mod 264, as two 32-bit words with least significant word first. (Regarding converting between streams of bytes and 32-bit words, the convention is little-endian; see Note 9.48.) Let m be the number of 512-bit blocks in the resulting string (b + r + 64 = 512m =
32 ·16m). The formatted input consists of 16m 32-bit words: x0x1 ...x16m−1. Initialize: (H1,H2,H3,H4) ← (h1,h2,h3,h4).
3.Processing. For each i from 0 to m − 1, copy the ith block of 16 32-bit words into temporary storage: X[j] ← x16i+j, 0 ≤ j ≤ 15, then process these as below in three 16-step rounds before updating the chaining variables:
(initialize working variables) (A,B,C,D) ← (H1,H2,H3,H4). (Round 1) For j from 0 to 15 do the following:
t ← (A + f(B,C,D) + X[z[j]] + y[j]), (A,B,C,D) ← (D,t ← s[j],B,C). (Round 2) For j from 16 to 31 do the following:
t ← (A + g(B,C,D) + X[z[j]] + y[j]), (A,B,C,D) ← (D,t ← s[j]),B,C). (Round 3) For j from 32 to 47 do the following:
t ← (A + h(B,C,D) + X[z[j]] + y[j]), (A,B,C,D) ← (D,t ← s[j]),B,C). (update chaining values) (H1,H2,H3,H4) ← (H1 +A,H2 +B,H3 +C,H4 +D).
4.Completion. The final hash-value is the concatenation: H1||H2||H3||H4
(with first and last bytes the lowand high-order bytes of H1, H4, respectively).
9.50Remark (MD4 collisions) Collisions have been found for MD4 in 220 compression function computations (cf. Table 9.3). For this reason, MD4 is no longer recommended for use as a collision-resistant hash function. While its utility as a one-way function has not been studied in light of this result, it is prudent to expect a preimage attack on MD4 requiring fewer than 2128 operations will be found.

§9.4 Unkeyed hash functions (MDCs) |
347 |
(ii) MD5
MD5 (Algorithm 9.51) was designed as a strengthened version of MD4, prior to actual MD4 collisions being found. It has enjoyed widespread use in practice. It has also now been found to have weaknesses (Remark 9.52).
The changes made to obtain MD5 from MD4 are as follows:
1.addition of a fourth round of 16 steps, and a Round 4 function
2.replacement of the Round 2 function by a new function
3.modification of the access order for message words in Rounds 2 and 3
4.modification of the shift amounts (such that shifts differ in distinct rounds)
5.use of unique additive constants in each of the 4 ×16 steps, based on the integer part of 232 ·sin(j) for step j (requiring overall, 256 bytes of storage)
6.addition of output from the previous step into each of the 64 steps.
9.51Algorithm MD5 hash function
INPUT: bitstring x of arbitrary bitlength b ≥ 0. (For notation, see Table 9.7.) OUTPUT: 128-bit hash-code of x. (See Table 9.6 for test vectors.)
MD5 is obtained from MD4 by making the following changes.
def
1. Notation. Replace the Round 2 function by: g(u,v,w) = uw vw.
def
Define a Round 4 function: k(u,v,w) = v (u w). 2. Definition of constants. Redefine unique additive constants:
y[j] = first 32 bits of binary value abs(sin(j+ 1)), 0 ≤ j ≤ 63, where j is in radians and “abs” denotes absolute value. Redefine access order for words in Rounds 2 and 3, and define for Round 4:
z[16..31] = [1,6,11,0,5,10,15,4,9,14,3,8,13,2,7,12], z[32..47] = [5,8,11,14,1,4,7,10,13,0,3,6,9,12,15,2], z[48..63] = [0,7,14,5,12,3,10,1,8,15,6,13,4,11,2,9]. Redefine number of bit positions for left shifts (rotates):
s[0..15] = [7,12,17,22,7,12,17,22,7,12,17,22,7,12,17,22], s[16..31] = [5,9,14,20,5,9,14,20,5,9,14,20,5,9,14,20], s[32..47] = [4,11,16,23,4,11,16,23,4,11,16,23,4,11,16,23], s[48..63] = [6,10,15,21,6,10,15,21,6,10,15,21,6,10,15,21].
3.Preprocessing. As in MD4.
4. Processing. In each of Rounds 1, 2, and 3, replace “ B ← (t ← s[j])” by “ B ← B + (t ← s[j])”. Also, immediately following Round 3 add:
(Round 4) For j from 48 to 63 do the following:
t ← (A+k(B,C,D)+X[z[j]]+y[j]), (A,B,C,D) ← (D,B+(t ← s[j]),B,C).
5.Completion. As in MD4.
9.52Remark (MD5 compression function collisions) While no collisions for MD5 have yet been found (cf. Table 9.3), collisions have been found for the MD5 compression function. More specifically, these are called collisions for random IV. (See §9.7.2, and in particular Definition 9.97 and Note 9.98.)

348 |
Ch. 9 Hash Functions and Data Integrity |
(iii) SHA-1
The Secure Hash Algorithm (SHA-1), based on MD4, was proposed by the U.S. National Institute for Standards and Technology (NIST) for certain U.S. federal government applications. The main differences of SHA-1 from MD4 are as follows:
1.The hash-value is 160 bits, and five (vs. four) 32-bit chaining variables are used.
2.The compression function has four rounds instead of three, using the MD4 step functions f, g, and h as follows: f in the first, g in the third, and h in both the second and fourth rounds. Each round has 20 steps instead of 16.
3.Within the compression function, each 16-word message block is expanded to an 80word block, by a process whereby each of the last 64 of the 80 words is the XOR of 4 words from earlier positions in the expanded block. These 80 words are then input one-word-per-step to the 80 steps.
4.The core step is modified as follows: the only rotate used is a constant 5-bit rotate; the fifth working variable is added into each step result; message words from the expanded message block are accessed sequentially; and C is updated as B rotated left 30 bits, rather than simply B.
5.SHA-1 uses four non-zero additive constants, whereas MD4 used three constants only two of which were non-zero.
The byte ordering used for converting between streams of bytes and 32-bit words in the official SHA-1 specification is big-endian (see Note 9.48); this differs from MD4 which is little-endian.
9.53Algorithm Secure Hash Algorithm – revised (SHA-1)
INPUT: bitstring x of bitlength b ≥ 0. (For notation, see Table 9.7.) OUTPUT: 160-bit hash-code of x. (See Table 9.6 for test vectors.)
SHA-1 is defined (with reference to MD4) by making the following changes.
1.Notation. As in MD4.
2.Definition of constants. Define a fifth IV to match those in MD4: h5 = 0xc3d2e1f0. Define per-round integer additive constants: y1 = 0x5a827999, y2 = 0x6ed9eba1, y3 = 0x8f1bbcdc, y4 = 0xca62c1d6. (No order for accessing source words, or specification of bit positions for left shifts is required.)
3.Overall preprocessing. Pad as in MD4, except the final two 32-bit words specifying the bitlength b is appended with most significant word preceding least significant.
As in MD4, the formatted input is 16m 32-bit words: x0x1 ...x16m−1. Initialize chaining variables: (H1,H2,H3,H4,H5) ← (h1,h2,h3,h4,h5).
4.Processing. For each i from 0 to m − 1, copy the ith block of sixteen 32-bit words into temporary storage: X[j] ← x16i+j, 0 ≤ j ≤ 15, and process these as below in four 20-step rounds before updating the chaining variables:
(expand 16-word block into 80-word block; let Xj denote X[j])
for j from 16 to 79, Xj ← (( Xj−3 Xj−8 Xj−14 Xj−16 ) ← 1). (initialize working variables) (A,B,C,D,E) ← (H1,H2,H3,H4,H5). (Round 1) For j from 0 to 19 do the following:
t ← ((A ← 5) + f(B,C,D) + E + Xj + y1), (A,B,C,D,E) ← (t,A,B ← 30,C,D). (Round 2) For j from 20 to 39 do the following:
t ← ((A ← 5) + h(B,C,D) + E + Xj + y2), (A,B,C,D,E) ← (t,A,B ← 30,C,D).

§9.4 Unkeyed hash functions (MDCs) |
349 |
(Round 3) For j from 40 to 59 do the following: t ← ((A ← 5) + g(B,C,D) + E + Xj + y3), (A,B,C,D,E) ← (t,A,B ← 30,C,D).
(Round 4) For j from 60 to 79 do the following: t ← ((A ← 5) + h(B,C,D) + E + Xj + y4), (A,B,C,D,E) ← (t,A,B ← 30,C,D).
(update chaining values)
(H1,H2,H3,H4,H5) ← (H1 + A,H2 + B,H3 + C,H4 + D,H5 + E).
5.Completion. The hash-value is: H1||H2||H3||H4||H5
(with first and last bytes the highand low-order bytes of H1, H5, respectively).
9.54Remark (security of SHA-1) Compared to 128-bit hash functions, the 160-bit hash-value of SHA-1 provides increased security against brute-force attacks. SHA-1 and RIPEMD160 (see §9.4.2(iv)) presently appear to be of comparable strength; both are considered stronger than MD5 (Remark 9.52). In SHA-1, a significant effect of the expansion of 16word message blocks to 80 words in the compression function is that any two distinct 16word blocks yield 80-word values which differ in a larger number of bit positions, significantly expanding the number of bit differences among message words input to the compression function. The redundancy added by this preprocessing evidently adds strength.
(iv)RIPEMD-160
RIPEMD-160 (Algorithm 9.55) is a hash function based on MD4, taking into account knowledge gained in the analysis of MD4, MD5, and RIPEMD. The overall RIPEMD-160 compression function maps 21-word inputs (5-word chaining variable plus 16-word message block, with 32-bit words) to 5-word outputs. Each input block is processed in parallel by distinct versions (the left line and right line) of the compression function. The 160-bit outputs of the separate lines are combined to give a single 160-bit output.
Notation |
Definition |
||||||||
|
|
|
|
|
|
|
|
|
|
f(u,v,w) |
u v w |
||||||||
g(u,v,w) |
uv |
|
|
|
|
|
|
|
|
uw |
|||||||||
h(u,v,w) |
(u |
|
) w |
||||||
v |
|||||||||
k(u,v,w) |
|
|
|
|
|
||||
uw vw |
|
|
|||||||
l(u,v,w) |
u (v |
|
) |
||||||
w |
|||||||||
Table 9.8: RIPEMD-160 round function definitions.
The RIPEMD-160 compression function differs from MD4 in the number of words of chaining variable, the number of rounds, the round functions themselves (Table 9.8), the order in which the input words are accessed, and the amounts by which results are rotated. The left and and right computation lines differ from each other in these last two items, in their additive constants, and in the order in which the round functions are applied. This design is intended to improve resistance against known attack strategies. Each of the parallel lines uses the same IV as SHA-1. When writing the IV as a bitstring, little-endian ordering is used for RIPEMD-160 as in MD4 (vs. big-endian in SHA-1; see Note 9.48).

350 |
Ch. 9 Hash Functions and Data Integrity |
9.55Algorithm RIPEMD-160 hash function
INPUT: bitstring x of bitlength b ≥ 0.
OUTPUT: 160-bit hash-code of x. (See Table 9.6 for test vectors.)
RIPEMD-160 is defined (with reference to MD4) by making the following changes.
1.Notation. See Table 9.7, with MD4 round functions f, g, h redefined per Table 9.8 (which also defines the new round functions k, l).
2.Definition of constants. Define a fifth IV: h5 = 0xc3d2e1f0. In addition:
(a)Use the MD4 additive constants for the left line, renamed: yL[j] = 0, 0 ≤ j ≤ 15; yL[j] = 0x5a827999, 16 ≤ j ≤ 31; yL[j] = 0x6ed9eba1, 32 ≤ j ≤ 47. Define two further constants (square roots of 5,7): yL[j] = 0x8f1bbcdc, 48 ≤ j ≤ 63; yL[j] = 0xa953fd4e, 64 ≤ j ≤ 79.
(b)Define five new additive constants for the right line (cube roots of 2,3,5,7):
yR[j] = 0x50a28be6, 0 ≤ j ≤ 15; yR[j] = 0x5c4dd124, 16 ≤ j ≤ 31;
yR[j] = 0x6d703ef3, 32 ≤ j ≤ 47; yR[j] = 0x7a6d76e9, 48 ≤ j ≤ 63; yR[j] = 0, 64 ≤ j ≤ 79.
(c)See Table 9.9 for constants for step j of the compression function: zL[j], zR[j] specify the access order for source words in the left and right lines; sL[j], sR[j] the number of bit positions for rotates (see below).
3.Preprocessing. As in MD4, with addition of a fifth chaining variable: H5 ← h5.
4.Processing. For each i from 0 to m − 1, copy the ith block of sixteen 32-bit words into temporary storage: X[j] ← x16i+j, 0 ≤ j ≤ 15. Then:
(a)Execute five 16-step rounds of the left line as follows:
(AL,BL,CL,DL,EL) ← (H1,H2,H3,H4,H5). (left Round 1) For j from 0 to 15 do the following:
t ← (AL + f(BL,CL,DL) + X[zL[j]] + yL[j]),
(AL,BL,CL,DL,EL) ← (EL,EL + (t ← sL[j]),BL,CL ← 10,DL). (left Round 2) For j from 16 to 31 do the following:
t ← (AL + g(BL,CL,DL) + X[zL[j]] + yL[j]),
(AL,BL,CL,DL,EL) ← (EL,EL + (t ← sL[j]),BL,CL ← 10,DL). (left Round 3) For j from 32 to 47 do the following:
t ← (AL + h(BL,CL,DL) + X[zL[j]] + yL[j]),
(AL,BL,CL,DL,EL) ← (EL,EL + (t ← sL[j]),BL,CL ← 10,DL). (left Round 4) For j from 48 to 63 do the following:
t ← (AL + k(BL,CL,DL) + X[zL[j]] + yL[j]),
(AL,BL,CL,DL,EL) ← (EL,EL + (t ← sL[j]),BL,CL ← 10,DL). (left Round 5) For j from 64 to 79 do the following:
t ← (AL + l(BL,CL,DL) + X[zL[j]] + yL[j]),
(AL,BL,CL,DL,EL) ← (EL,EL + (t ← sL[j]),BL,CL ← 10,DL).
(b)Execute in parallel with the above five rounds an analogous right line with (AR,BR,CR,DR,ER), yR[j], zR[j], sR[j] replacing the corresponding quantities with subscript L; and the order of the round functions reversed so that their order is: l, k, h, g, and f. Start by initializing the right line working variables:
(AR,BR,CR,DR,ER) ← (H1,H2,H3,H4,H5).
(c)After executing both the left and right lines above, update the chaining values
as follows: t ← H1, H1 ← H2 + CL + DR, H2 ← H3 + DL + ER, H3 ←
H4 + EL + AR, H4 ← H5 + AL + BR, H5 ← t + BL + CR.
5.Completion. The final hash-value is the concatenation: H1||H2||H3||H4||H5 (with first and last bytes the lowand high-order bytes of H1, H5, respectively).

§9.4 Unkeyed hash functions (MDCs) |
|
351 |
|||
|
|
|
|
|
|
|
Variable |
Value |
|
|
|
|
|
|
|
|
|
|
zL[ 0..15] |
[ 0, 1, 2, 3, 4, 5, 6, 7, 8, |
9,10,11,12,13,14,15] |
|
|
|
zL[16..31] |
[ 7, 4,13, 1,10, 6,15, 3,12, |
0, 9, 5, 2,14,11, 8] |
|
|
|
zL[32..47] |
[ 3,10,14, 4, 9,15, 8, 1, 2, |
7, 0, 6,13,11, 5,12] |
|
|
|
zL[48..63] |
[ 1, 9,11,10, 0, 8,12, 4,13, |
3, 7,15,14, 5, 6, 2] |
|
|
|
zL[64..79] |
[ 4, 0, 5, 9, 7,12, 2,10,14, |
1, 3, 8,11, 6,15,13] |
|
|
|
zR[ 0..15] |
[ 5,14, 7, 0, 9, 2,11, 4,13, 6,15, 8, 1,10, 3,12] |
|
||
|
zR[16..31] |
[ 6,11, 3, 7, 0,13, 5,10,14,15, 8,12, 4, |
9, 1, 2] |
|
|
|
zR[32..47] |
[15, 5, 1, 3, 7,14, 6, 9,11, 8,12, 2,10, |
0, 4,13] |
|
|
|
zR[48..63] |
[ 8, 6, 4, 1, 3,11,15, 0, 5,12, 2,13, 9, |
7,10,14] |
|
|
|
zR[64..79] |
[12,15,10, 4, 1, 5, 8, 7, 6, 2,13,14, 0, |
3, 9,11] |
|
|
|
sL[ 0..15] |
[11,14,15,12, 5, 8, 7, 9,11,13,14,15, 6, |
7, 9, 8] |
|
|
|
sL[16..31] |
[ 7, 6, 8,13,11, 9, 7,15, 7,12,15, 9,11, 7,13,12] |
|
||
|
sL[32..47] |
[11,13, 6, 7,14, 9,13,15,14, 8,13, 6, 5,12, 7, 5] |
|
||
|
sL[48..63] |
[11,12,14,15,14,15, 9, 8, 9,14, 5, 6, 8, 6, 5,12] |
|
||
|
sL[64..79] |
[ 9,15, 5,11, 6, 8,13,12, 5,12,13,14,11, 8, 5, 6] |
|
||
|
sR[ 0..15] |
[ 8, 9, 9,11,13,15,15, 5, 7, 7, 8,11,14,14,12, 6] |
|
||
|
sR[16..31] |
[ 9,13,15, 7,12, 8, 9,11, 7, 7,12, 7, 6,15,13,11] |
|
||
|
sR[32..47] |
[ 9, 7,15,11, 8, 6, 6,14,12,13, 5,14,13,13, 7, 5] |
|
||
|
sR[48..63] |
[15, 5, 8,11,14,14, 6,14, 6, 9,12, 9,12, 5,15, 8] |
|
||
|
sR[64..79] |
[ 8, 5,12, 9,12, 5,14, 6, 8,13, 6, 5,15,13,11,11] |
|
||
Table 9.9: RIPEMD-160 word-access orders and rotate counts (cf. Algorithm 9.55).
9.4.3 Hash functions based on modular arithmetic
The basic idea of hash functions based on modular arithmetic is to construct an iterated hash function using mod M arithmetic as the basis of a compression function. Two motivating factors are re-use of existing software or hardware (in public-key systems) for modular arithmetic, and scalability to match required security levels. Significant disadvantages, however, include speed (e.g., relative to the customized hash functions of §9.4.2), and an embarrassing history of insecure proposals.
MASH
MASH-1 (Modular Arithmetic Secure Hash, algorithm 1) is a hash function based on modular arithmetic. It has been proposed for inclusion in a draft ISO/IEC standard. MASH-1 involves use of an RSA-like modulus M, whose bitlength affects the security. M should be difficult to factor, and for M of unknown factorization, the security is based in part on the difficulty of extracting modular roots ( §3.5.2). The bitlength of M also determines the blocksize for processing messages, and the size of the hash-result (e.g., a 1025-bit modulus yields a 1024-bit hash-result). As a recent proposal, its security remains open to question (page 381). Techniques for reducing the size of the final hash-result have also been proposed, but their security is again undetermined as yet.

352 |
Ch. 9 Hash Functions and Data Integrity |
9.56Algorithm MASH-1 (version of Nov. 1995)
INPUT: data x of bitlength 0 ≤ b < 2n/2.
OUTPUT: n-bit hash of x (n is approximately the bitlength of the modulus M).
1.System setup and constant definitions. Fix an RSA-like modulus M = pq of bitlength m, where p and q are randomly chosen secret primes such that the factorization of
M is intractable. Define the bitlength n of the hash-result to be the largest multiple of 16 less than m (i.e., n = 16n < m). H0 = 0 is defined as an IV, and an n- bit integer constant A = 0xf0...0. “ ” denotes bitwise inclusive-OR; “ ” denotes bitwise exclusive-OR.
2.Padding, blocking, and MD-strengthening. Pad x with 0-bits, if necessary, to obtain a string of bitlength t·n/2 for the smallest possible t ≥ 1. Divide the padded text into (n/2)-bit blocks x1,... ,xt, and append a final block xt+1 containing the (n/2)-bit representation of b.
3.Expansion. Expand each xi to an n-bit block yi by partitioning it into (4-bit) nibbles and inserting four 1-bits preceding each, except for yt+1 wherein the inserted nibble is 1010 (not 1111).
4.Compression function processing. For 1 ≤ i ≤ t+1, map two n-bit inputs (Hi−1, yi) to one n-bit output as follows: Hi ← ((((Hi−1 yi) A)2 mod M) n) Hi−1. Here n denotes keeping the rightmost n bits of the m-bit result to its left.
5.Completion. The hash is the n-bit block Ht+1.
MASH-2 is defined as per MASH-1 with the exponent e = 2 used for squaring in the compression function processing stage (step 4) replaced with e = 28 + 1.
9.5 Keyed hash functions (MACs)
Keyed hash functions whose specific purpose is message authentication are called message authentication code (MAC) algorithms. Compared to the large number of MDC algorithms, prior to 1995 relatively few MAC algorithms had been proposed, presumably because the original proposals, which were widely adopted in practice, were adequate. Many of these are for historical reasons block-cipher based. Those with relatively short MAC bitlengths (e.g., 32-bits for MAA) or short keys (e.g., 56 bits for MACs based on DES-CBC) may still offer adequate security, depending on the computational resources available to adversaries, and the particular environment of application.
Many iterated MACs can be described as iterated hash functions (see Figure 9.2, and equation (9.1) on page 333). In this case, the MAC key is generally part of the output transformation g; it may also be an input to the compression function in the first iteration, and be involved in the compression function f at every stage.
Fact 9.57 is a general result giving an upper bound on the security of MACs.
9.57Fact (birthday attack on MACs) Let h be a MAC algorithm based on an iterated compression function, which has n bits of internal chaining variable, and is deterministic (i.e., the m-bit result is fully determined by the message). Then MAC forgery is possible using O(2n/2) known text-MAC pairs plus a number v of chosen text-MAC pairs which (depending on h) is between 1 and about 2n−m.

§9.5 Keyed hash functions (MACs) |
353 |
9.5.1 MACs based on block ciphers
CBC-based MACs
The most commonly used MAC algorithm based on a block cipher makes use of cipher- block-chaining (§7.2.2(ii)). When DES is used as the block cipher E, n = 64 in what follows, and the MAC key is a 56-bit DES key.
9.58Algorithm CBC-MAC
INPUT: data x; specification of block cipher E; secret MAC key k for E. OUTPUT: n-bit MAC on x (n is the blocklength of E).
1.Padding and blocking. Pad x if necessary (e.g., using Algorithm 9.30). Divide the padded text into n-bit blocks denoted x1,... ,xt.
2.CBC processing. Letting Ek denote encryption using E with key k, compute the block Ht as follows: H1 ← Ek(x1); Hi ← Ek(Hi−1 xi), 2 ≤ i ≤ t. (This is standard cipher-block-chaining, IV = 0, discarding ciphertext blocks Ci = Hi.)
3.Optional process to increase strength of MAC. Using a second secret key k =k, optionally compute: Ht ← Ek−1(Ht), Ht ← Ek(Ht). (This amounts to using twokey triple-encryption on the last block; see Remark 9.59.)
4.Completion. The MAC is the n-bit block Ht.
|
x1 |
|
x2 |
|
x3 |
|
xt |
0 |
|
H1 |
|
H2 |
H3 |
Ht−1 |
|
|
|
|
|
||||
k |
E |
k |
E |
k |
E |
k |
E |
Ht
k 
 E-1
E-1
optional
k 
 E
E
H
Figure 9.6: CBC-based MAC algorithm.
For CBC-MAC with n = 64 = m, Fact 9.57 applies with v = 1.
9.59Remark (CBC-MAC strengthening) The optional process reduces the threat of exhaustive key search, and prevents chosen-text existential forgery (Example 9.62), without impacting the efficiency of the intermediate stages as would using two-key triple-encryption

354 |
Ch. 9 Hash Functions and Data Integrity |
throughout. Alternatives to combat such forgery include prepending the input with a length block before the MAC computation; or using key K to encrypt the length m yielding K = EK(m), before using K as the key to MAC the message.
9.60Remark (truncated MAC outputs) Exhaustive attack may, depending on the unicity distance of the MAC, be precluded (information-theoretically) by using less than n bits of the
final output as the m-bit MAC. (This must be traded off against an increase in the probability of randomly guessing the MAC: 2−m.) For m = 32 and E = DES, an exhaustive attack reduces the key space to about 224 possibilities. However, even for m < n, a second
text-MAC pair almost certainly determines a unique MAC key.
9.61Remark (CBC-MAC IV) While a random IV in CBC encryption serves to prevent a codebook attack on the first ciphertext block, this is not a concern in a MAC algorithm.
9.62Example (existential forgery of CBC-MAC) While CBC-MAC is secure for messages of a fixed number t of blocks, additional measures (beyond simply adding a trailing lengthblock) are required if variable length messages are allowed, otherwise (adaptive chosen-
text) existential forgery is possible as follows. Assume xi is an n-bit block, and let b denote the n-bit binary representation of b. Let (x1,M1) be a known text-MAC pair, and request the MAC M2 for the one-block message x2 = M1; then M2 = Ek(Ek(x1)) is also the MAC for the 2-block message (x1||0). As a less trivial example, given two known text-MAC pairs (x1,H1), (x2,H2) for one-block messages x1,x2, and requesting the MAC M on a chosen 2-block third message (x1||z) for a third text-MAC pair ((x1||z),M), then Hi = Ek(xi), M = Ek(H1 z), and the MAC for the new 2-block message X = x2||(H1 z H2) is known – it is M also. Moreover, MD-strengthening (Algorithm 9.26) does not address the problem: assume padding by Algorithm 9.29, replace the third message above by the 3-block message (x1||64||z), note
Hi = Ek(Ek(xi) 64), M3 = Ek(Ek(Ek(Ek(x1) 64) z) 192),
and M3 is also the MAC for the new 3-block message X = (x2||64||H1 H2 z).
9.63Example (RIPE-MAC) RIPE-MAC is a variant of CBC-MAC. Two versions RIPEMAC1 and RIPE-MAC3, both producing 64-bit MACs, differ in their internal encryption function E being either single DES or two-key triple-DES, respectively, requiring a 56or 112-bit key k (cf. Remark 9.59). Differences from Algorithm 9.58 are as follows: the compression function uses a non-invertible chaining best described as CBC with data feed-
forward: Hi ← Ek(Hi−1 xi) xi; after padding using Algorithm 9.30, a final 64-bit length-block (giving bitlength of original input) is appended; the optional process of Algorithm 9.58 is mandatory with final output block encrypted using key k derived by complementing alternating nibbles of k: for k = k0 ...k63 a 56-bit DES key with parity bits k7k15 ...k63, k = k 0xf0f0f0f0f0f0f0f0.
9.5.2 Constructing MACs from MDCs
A common suggestion is to construct a MAC algorithm from an MDC algorithm, by simply including a secret key k as part of the MDC input. A concern with this approach is that implicit but unverified assumptions are often made about the properties that MDCs have; in particular, while most MDCs are designed to provide one-wayness or collision resistance,
§9.5 Keyed hash functions (MACs) |
355 |
the requirements of a MAC algorithm differ (Definition 9.7). Even in the case that a oneway hash function precludes recovery of a secret key used as a partial message input (cf. partial-preimage resistance, page 331), this does not guarantee the infeasibility of producing MACs for new inputs. The following examples suggest that construction of a MAC from a hash function requires careful analysis.
9.64 Example (secret prefix method) Consider a message x = x1x2 ...xt and an iterated MDC h with compression function f, with definition: H0 = IV,Hi = f(Hi−1,xi); h(x) = Ht. (1) Suppose one attempts to use h as a MAC algorithm by prepending a secret key k, so that the proposed MAC on x is M = h(k||x). Then, extending the message x by an arbitrary single block y, one may deduce M = h(k||x||y) as f(M,y) without knowing the secret key k (the original MAC M serves as chaining variable). This is true even for hash functions whose preprocessing pads inputs with length indicators (e.g., MD5); in this case, the padding/length-block z for the original message x would appear as part of the extended message, x||z||y, but a forged MAC on the latter may nonetheless be deduced. (2) For similar reasons, it is insecure to use an MDC to construct a MAC algorithm by using the secret MAC key k as IV. If k comprises the entire first block, then for efficiency f(IV,k) may be precomputed, illustrating that an adversary need only find a k (not necessarily k) such that f(IV,k) = f(IV,k ); this is equivalent to using a secret IV.
9.65Example (secret suffix method) An alternative proposal is to use a secret key as a suffix, i.e., the n-bit MAC on x is M = h(x||k). In this case, a birthday attack applies (§9.7.1). An adversary free to choose the message x (or a prefix thereof) may, in O( 2n/2) operations, find a pair of messages x,x for which h(x) = h(x ). (This can be done off-line, and does not require knowledge of k; the assumption here is that n is the size of both the chaining
variable and the final output.) Obtaining a MAC M on x by legitimate means then allows an adversary to produce a correct text-MAC pair (x ,M) for a new message x . Note that
this method essentially hashes and then encrypts the hash-value in the final iteration; in this
weak form of MAC, the MAC-value depends only on the last chaining value, and the key is used in only one step.
The above examples suggest that a MAC key should be involved at both the start and the end of MAC computations, leading to Example 9.66.
9.66 Example (envelope method with padding) For a key k and MDC h, compute the MAC on a message x as: hk(x) = h(k ||p||x||k). Here p is a string used to pad k to the length of one block, to ensure that the internal computation involves at least two iterations. For example, if h is MD5 and k is 128 bits, p is a 384-bit pad string.
Due to both a certificational attack against the MAC construction of Example 9.66 and theoretical support for that of Example 9.67 (see page 382), the latter construction is favored.
9.67Example (hash-based MAC) For a key k and MDC h, compute the MAC on a message x as HMAC(x) = h(k ||p1 ||h(k ||p2 ||x)), where p1, p2 are distinct strings of sufficient
length to pad k out to a full block for the compression function. The overall construction is quite efficient despite two calls to h, since the outer execution processes only (e.g., if h is MD5) a two-block input, independent of the length of x.
Additional suggestions for achieving MAC-like functionality by combining MDCs and encryption are discussed in §9.6.5.

356 |
Ch. 9 Hash Functions and Data Integrity |
9.5.3 Customized MACs
Two algorithms designed for the specific purpose of message authentication are discussed in this section: MAA and MD5-MAC.
Message Authenticator Algorithm (MAA)
The Message Authenticator Algorithm (MAA), dating from 1983, is a customized MAC algorithm for 32-bit machines, involving 32-bit operations throughout. It is specified as Algorithm 9.68 and illustrated in Figure 9.7. The main loop consists of two parallel interdependent streams of computation. Messages are processed in 4-byte blocks using 8 bytes of chaining variable. The execution time (excluding key expansion) is proportional to message length; as a rough guideline, MAA is twice as slow as MD4.
9.68Algorithm Message Authenticator Algorithm (MAA)
INPUT: data x of bitlength 32j, 1 ≤ j ≤ 106; secret 64-bit MAC key Z = Z[1]..Z[8]. OUTPUT: 32-bit MAC on x.
1. Message-independent key expansion. Expand key Z to six 32-bit quantities X, Y , V , W, S, T (X,Y are initial values; V,W are main loop variables; S,T are appended to the message) as follows.
1.1First replace any bytes 0x00 or 0xff in Z as follows. P ← 0; for i from 1 to 8 (P ← 2P; if Z[i] = 0x00 or 0xff then (P ← P + 1; Z[i] ← Z[i] OR P)).
1.2Let J and K be the first 4 bytes and last 4 bytes of Z, and compute:4 X ← J4 (mod 232 − 1) J4 (mod 232 − 2)
Y ← [K5 (mod 232 − 1) K5 (mod 232 − 2)](1 + P)2 (mod 232 − 2)
V ← J6 (mod 232 − 1) J6 (mod 232 − 2) W ← K7 (mod 232 − 1) K7 (mod 232 − 2) S ← J8 (mod 232 − 1) J8 (mod 232 − 2) T ← K9 (mod 232 − 1) K9 (mod 232 − 2)
1.3Process the 3 resulting pairs (X,Y ), (V,W), (S,T) to remove any bytes 0x00, 0xff as for Z earlier. Define the AND-OR constants: A = 0x02040801, B = 0x00804021, C = 0xbfef7fdf, D = 0x7dfefbff.
2.Initialization and preprocessing. Initialize the rotating vector: v ← V , and the chaining variables: H1 ← X, H2 ← Y . Append the key-derived blocks S, T to x, and let x1 ...xt denote the resulting augmented segment of 32-bit blocks. (The final 2 blocks of the segment thus involve key-derived secrets.)
3.Block processing. Process each 32-bit block xi (for i from 1 to t) as follows. v ← (v ← 1), U ← (v W)
t1 ← (H1 xi) ×1 (((H2 xi) + U) OR A) AND C) t2 ← (H2 xi) ×2 (((H1 xi) + U) OR B) AND D)
H1 ← t1, H2 ← t2
where ×i denotes special multiplication mod 232 − i as noted above (i = 1 or 2); “+” is addition mod 232; and “ ← 1” denotes rotation left one bit. (Each combined AND-OR operation on a 32-bit quantity sets 4 bits to 1, and 4 to 0, precluding 0- multipliers.)
4. Completion. The resulting MAC is: H = H1 H2.
4 |
In ISO 8731-2, a well-defined but unconventional definition of multiplication mod |
32 |
− 2 is specified, pro- |
|
2 |
ducing 32-bit results which in some cases are 232 − 1 or 232 − 2; for this reason, specifying e.g., J6 here may be ambiguous; the standard should be consulted for exact details.

§9.5 Keyed hash functions (MACs) |
357 |
||
message x |
key (J,K) |
||
|
|
64 |
[from message x] |
|
|
||
|
|
|
|
|
|
|
|
key expansion
|
|
|
|
S |
|
|
|
|
|
|
T |
V |
Y |
|
|
|
|
|
||
|
|
|
|
|
|
|
x1 |
x2 |
x3 |
··· xt−2 xt−1 |
xt |
|
|
|
|
|
|
X |
|
W |
|
V |
xi |
xi |
i= 1 |
i= 1 |
H1 |
|
U |
H2 |
|
|
||
i>1 |
|
|
i>1 |
|
+ |
+ |
|
B |
OR |
OR |
A |
delay i←i+1 |
|
|
i←i+1 delay |
D |
AND |
AND |
C |
(mod 232 −1) |
|
|
(mod 232 −2) |
H1 |
|
|
H2 |
Figure 9.7: The Message Authenticator Algorithm (MAA).
Since the relatively complex key expansion stage is independent of the message, a onetime computation suffices for a fixed key. The mixing of various operations (arithmetic mod 232 − i, for i = 0,1 and 2; XOR; and nonlinear AND-OR computations) is intended to strengthen the algorithm against arithmetic cryptanalytic attacks.
MD5-MAC
A more conservative approach (cf. Example 9.66) to building a MAC from an MDC is to arrange that the MAC compression function itself depend on k, implying the secret key be involved in all intervening iterations; this provides additional protection in the case that weaknesses of the underlying hash function become known. Algorithm 9.69 is such a technique, constructed using MD5. It provides performance close to that of MD5 (5-20% slower in software).

358 |
Ch. 9 Hash Functions and Data Integrity |
9.69Algorithm MD5-MAC
INPUT: bitstring x of arbitrary bitlength b ≥ 0; key k of bitlength ≤ 128. OUTPUT: 64-bit MAC-value of x.
MD5-MAC is obtained from MD5 (Algorithm 9.51) by the following changes.
1.Constants. The constants Ui and Ti are as defined in Example 9.70.
2.Key expansion.
(a)If k is shorter than 128 bits, concatenate k to itself a sufficient number of times, and redefine k to be the leftmost 128 bits.
(b)Let MD5 denote MD5 with both padding and appended length omitted. Expand
k into three 16-byte subkeys K0, K1, and K2 as follows: for i from 0 to 2,
Ki ← MD5(k Ui k).
(c)Partition each of K0 and K1 into four 32-bit substrings Kj[i], 0 ≤ i ≤ 3.
3.K0 replaces the four 32-bit IV ’s of MD5 (i.e., hi = K0[i]).
4.K1[i] is added mod 232 to each constant y[j] used in Round i of MD5.
5.K2 is used to construct the following 512-bit block, which is appended to the padded input x subsequent to the regular padding and length block as defined by MD5:
K2 K2 T0 K2 T1 K2 T2.
6.The MAC-value is the leftmost 64 bits of the 128-bit output from hashing this padded and extended input string using MD5 with the above modifications.
9.70Example (MD5-MAC constants/test vectors) The 16-byte constants Ti and three test vectors (x, MD5-MAC(x)) for key k = 00112233445566778899aabbccddeeff are given below. (The Ti themselves are derived using MD5 on pre-defined constants.) With subscripts in Ti taken mod 3, the 96-byte constants U0, U1, U2 are defined:
Ui = Ti Ti+1 Ti+2 Ti Ti+1 Ti+2.
T0: 97 ef 45 ac 29 0f 43 cd 45 7e 1b 55 1c 80 11 34 T1: b1 77 ce 96 2e 72 8e 7c 5f 5a ab 0a 36 43 be 18 T2: 9d 21 b4 21 bc 87 b9 4d a2 9d 27 bd c7 5b d7 c3
("", |
1f1ef2375cc0e0844f98e7e811a34da8) |
("abc", |
e8013c11f7209d1328c0caa04fd012a6) |
("abcdefghijklmnopqrstuvwxyz", 9172867eb60017884c6fa8cc88ebe7c9)
9.5.4 MACs for stream ciphers
Providing data origin authentication and data integrity guarantees for stream ciphers is particularly important due to the fact that bit manipulations in additive stream-ciphers may directly result in predictable modifications of the underlying plaintext (e.g., Example 9.83). While iterated hash functions process message data a block at a time (§9.3.1), MACs designed for use with stream ciphers process messages either one bit or one symbol (block) at a time, and those which may be implemented using linear feedback shift registers (LFSRs) are desirable for reasons of efficiency.
One such MAC technique, Algorithm 9.72 below, is based on cyclic redundancy codes (cf. Example 9.80). In this case, the polynomial division may be implemented using an LFSR. The following definition is of use in what follows.

§9.6 Data integrity and message authentication |
359 |
9.71Definition A (b,m) hash-family H is a collection of hash functions mapping b-bit messages to m-bit hash-values. A (b,m) hash-family is ε-balanced if for all messages B = 0 and all m-bit hash-values c, probh(h(B) = c)) ≤ ε, where the probability is over all randomly selected functions h H.
9.72Algorithm CRC-based MAC
INPUT: b-bit message B; shared key (see below) between MAC source and verifier. OUTPUT: m-bit MAC-value on B (e.g., m = 64).
1.Notation. Associate B = Bb−1 ...B1B0 with the polynomial B(x) = bi=0−1 Bixi.
2.Selection of MAC key.
(a)Select a random binary irreducible polynomial p(x) of degree m. (This represents randomly drawing a function h from a (b,m) hash-family.)
(b)Select a random m-bit one-time key k (to be used as a one-time pad).
The secret MAC key consists of p(x) and k, both of which must be shared a priori between the MAC originator and verifier.
3.Compute h(B) = coef (B(x) · xm mod p(x)), the m-bit string of coefficients from the degree m − 1 remainder polynomial after dividing B(x) · xm by p(x).
4.The m-bit MAC-value for B is: h(B) k.
9.73Fact (security of CRC-based MAC) For any values b and m > 1, the hash-family resulting from Algorithm 9.72 is ε-balanced for ε = (b + m)/(2m−1), and the probability of MAC forgery is at most ε.
9.74Remark (polynomial reuse) The hash function h in Algorithm 9.72 is determined by the irreducible polynomial p(x). In practice, p(x) may be re-used for different messages (e.g., within a session), but for each message a new random key k should be used.
9.6Data integrity and message authentication
This section considers the use of hash functions for data integrity and message authentication. Following preliminary subsections, respectively, providing background definitions and distinguishing non-malicious from malicious threats to data integrity, three subsequent subsections consider three basic approaches to providing data integrity using hash functions, as summarized in Figure 9.8.
9.6.1 Background and definitions
This subsection discusses data integrity, data origin authentication (message authentication), and transaction authentication.
Assurances are typically required both that data actually came from its reputed source (data origin authentication), and that its state is unaltered (data integrity). These issues cannot be separated – data which has been altered effectively has a new source; and if a source cannot be determined, then the question of alteration cannot be settled (without reference to a source). Integrity mechanisms thus implicitly provide data origin authentication, and vice versa.
360 |
Ch. 9 Hash Functions and Data Integrity |
|
|
secret key |
(a) MAC only |
message |
MAC |
|
algorithm |
|
|
|
|
|
message MAC |
unsecured channel |
(b) MDC |
message |
|
MDC |
|
& encipherment |
|
algorithm |
|
|
|
|
secret key |
||
|
|
|
|
|
|
message |
MDC |
encryption |
|
|
algorithm |
|
||
|
|
|
|
|
|
message |
MDC |
|
unsecured channel |
|
encrypted |
|
|
|
(c) MDC & authentic |
message |
|
MDC |
|
channel |
|
algorithm |
|
|
|
|
|
||
|
|
|
MDC |
authentic channel |
|
|
|
|
unsecured channel |
Figure 9.8: Three methods for providing data integrity using hash functions. The second method provides
encipherment simultaneously.

§9.6 Data integrity and message authentication |
361 |
(i)Data integrity
9.75Definition Data integrity is the property whereby data has not been altered in an unauthorized manner since the time it was created, transmitted, or stored by an authorized source.
Verification of data integrity requires that only a subset of all candidate data items satisfies particular criteria distinguishing the acceptable from the unacceptable. Criteria allowing recognizability of data integrity include appropriate redundancy or expectation with respect to format. Cryptographic techniques for data integrity rely on either secret information or authentic channels (§9.6.4).
The specific focus of data integrity is on the bitwise composition of data (cf. transaction authentication below). Operations which invalidate integrity include: insertion of bits, including entirely new data items from fraudulent sources; deletion of bits (short of deleting entire data items); re-ordering of bits or groups of bits; inversion or substitution of bits; and any combination of these, such as message splicing (re-use of proper substrings to construct new or altered data items). Data integrity includes the notion that data items are complete. For items split into multiple blocks, the above alterations apply analogously with blocks envisioned as substrings of a contiguous data string.
(ii)Data origin authentication (message authentication)
9.76Definition Data origin authentication is a type of authentication whereby a party is corroborated as the (original) source of specified data created at some (typically unspecified) time in the past.
By definition, data origin authentication includes data integrity.
9.77Definition Message authentication is a term used analogously with data origin authentication. It provides data origin authentication with respect to the original message source (and data integrity, but no uniqueness and timeliness guarantees).
Methods for providing data origin authentication include the following:
1.message authentication codes (MACs)
2.digital signature schemes
3.appending (prior to encryption) a secret authenticator value to encrypted text. 5
Data origin authentication mechanisms based on shared secret keys (e.g., MACs) do not allow a distinction to be made between the parties sharing the key, and thus (as opposed to digital signatures) do not provide non-repudiation of data origin – either party can equally originate a message using the shared key. If resolution of subsequent disputes is a potential requirement, either an on-line trusted third party in a notary role, or asymmetric techniques (see Chapter 11) may be used.
While MACs and digital signatures may be used to establish that data was generated by a specified party at some time in the past, they provide no inherent uniqueness or timeliness guarantees. These techniques alone thus cannot detect message re-use or replay, which is necessary in environments where messages may have renewed effect on second or subsequent use. Such message authentication techniques may, however, be augmented to provide these guarantees, as next discussed.
5Such a sealed authenticator (cf. a MAC, sometimes called an appended authenticator) is used along with an encryption method which provides error extension. While this resembles the technique of using encryption and an MDC (§9.6.5), whereas the MDC is a (known) function of the plaintext, a sealed authenticator is itself secret.

362 |
Ch. 9 Hash Functions and Data Integrity |
(iii)Transaction authentication
9.78Definition Transaction authentication denotes message authentication augmented to additionally provide uniqueness and timeliness guarantees on data (thus preventing undetectable message replay).
The uniqueness and timeliness guarantees of Definition 9.78 are typically provided by appropriate use of time-variant parameters (TVPs). These include random numbers in challenge-response protocols, sequence numbers, and timestamps as discussed in §10.3.1. This may be viewed as a combination of message authentication and entity authentication (Definition 10.1). Loosely speaking,
message authentication + TVP = transaction authentication.
As a simple example, sequence numbers included within the data of messages authenticated by a MAC or digital signature algorithm allow replay detection (see Remark 9.79), and thus provide transaction authentication.
As a second example, for exchanges between two parties involving two or more messages, transaction authentication on each of the second and subsequent messages may be provided by including in the message data covered by a MAC a random number sent by the other party in the previous message. This chaining of messages through random numbers prevents message replay, since any MAC values in replayed messages would be incorrect (due to disagreement between the random number in the replayed message, and the most recent random number of the verifier).
Table 9.10 summarizes the properties of these and other types of authentication. Authentication in the broadest sense encompasses not only data integrity and data origin authentication, but also protection from all active attacks including fraudulent representation and message replay. In contrast, encryption provides protection only from passive attacks.
→ Property |
identification |
data |
timeliness or |
defined |
↓ Type of authentication |
of source |
integrity |
uniqueness |
in |
|
|
|
|
|
message authentication |
yes |
yes |
— |
§9.6.1 |
transaction authentication |
yes |
yes |
yes |
§9.6.1 |
entity authentication |
yes |
— |
yes |
§10.1.1 |
key authentication |
yes |
yes |
desirable |
§12.2.1 |
Table 9.10: Properties of various types of authentication.
9.79Remark (sequence numbers and authentication) Sequence numbers may provide uniqueness, but not (real-time) timeliness, and thus are more appropriate to detect message replay than for entity authentication. Sequence numbers may also be used to detect the deletion of entire messages; they thus allow data integrity to be checked over an ongoing sequence of messages, in addition to individual messages.
9.6.2Non-malicious vs. malicious threats to data integrity
The techniques required to provide data integrity on noisy channels differ substantially from those required on channels subject to manipulation by adversaries.
Checksums provide protection against accidental or non-malicious errors on channels which are subject to transmission errors. The protection is non-cryptographic, in the sense

§9.6 Data integrity and message authentication |
363 |
that neither secret keys nor secured channels are used. Checksums generalize the idea of a parity bit by appending a (small) constant amount of message-specific redundancy. Both the data and the checksum are transmitted to a receiver, at which point the same redundancy computation is carried out on the received data and compared to the received checksum. Checksums can be used either for error detection or in association with higher-level errorrecovery strategies (e.g., protocols involving acknowledgements and retransmission upon failure). Trivial examples include an arithmetic checksum (compute the running 32-bit sum of all 32-bit data words, discarding high-order carries), and a simple XOR (XOR all 32bit words in a data string). Error-correcting codes go one step further than error-detecting codes, offering the capability to actually correct a limited number of errors without retransmission; this is sometimes called forward error correction.
9.80Example (CRCs) Cyclic redundancy codes or CRCs are commonly used checksums. A k-bit CRC algorithm maps arbitrary length inputs into k-bit imprints, and provides significantly better error-detection capability than k-bit arithmetic checksums. The algorithm is based on a carefully chosen (k + 1)-bit vector represented as a binary polynomial; for k = 16, a commonly used polynomial (CRC-16) is g(x) = 1+x2 +x15 +x16. A t-bit data input is represented as a binary polynomial d(x) of degree t − 1, and the CRC-value corresponding to d(x) is the 16-bit string represented by the polynomial remainder c(x) when x16 ·d(x) is divided by g(x);6 polynomial remaindering is analogous to computing integer remainders by long division. For all messages d(x) with t < 32 768, CRC-16 can detect
all errors that consist of only a single bit, two bits, three bits, or any odd number of bits, all burst errors of bitlength 16 or less, 99.997% (1 −2−15) of 17-bit burst errors, and 99.998% (1 −2−16) of all bursts 18 bits or longer. (A burst error of bitlength b is any bitstring of exactly b bits beginning and ending with a 1.) Analogous to the integer case, other data strings
d (x) yielding the same remainder as d(x) can be trivially found by adding multiples of the divisor g(x) to d(x), or inserting extra blocks representing a multiple of g(x). CRCs thus do not provide one-wayness as required for MDCs; in fact, CRCs are a class of linear (error correcting) codes, with one-wayness comparable to an XOR-sum.
While of use for detection of random errors, k-bit checksums are not of cryptographic use, because typically a data string checksumming to any target value can be easily created. One method is to simply insert or append to any data string of choice a k-bit correctingblock c which has the effect of correcting the overall checksum to the desired value. For example, for the trivial XOR checksum, if the target checksum is c , insert as block c the XOR of c and the XOR of all other blocks.
In contrast to checksums, data integrity mechanisms based on (cryptographic) hash functions are specifically designed to preclude undetectable intentional modification. The hash-values resulting are sometimes called integrity check values (ICV), or cryptographic check values in the case of keyed hash functions. Semantically, it should not be possible for an adversary to take advantage of the willingness of users to associate a given hash output with a single, specific input, despite the fact that each such output typically corresponds to a large set of inputs. Hash functions should exhibit no predictable relationships or correlations between inputs and outputs, as these may allow adversaries to orchestrate unintended associations.
6A modification is typically used in practice (e.g., complementing c(x)) to address the combination of an input d(x) = 0 and a “stuck-at-zero” communications fault yielding a successful CRC check.

364 |
Ch. 9 Hash Functions and Data Integrity |
9.6.3 Data integrity using a MAC alone
Message Authentication Codes (MACs) as discussed earlier are designed specifically for applications where data integrity (but not necessarily privacy) is required. The originator of a message x computes a MAC hk(x) over the message using a secret MAC key k shared with the intended recipient, and sends both (effectively x || hk(x)). The recipient determines by some means (e.g., a plaintext identifier field) the claimed source identity, separates the received MAC from the received data, independently computes a MAC over this data using the shared MAC key, and compares the computed MAC to the received MAC. The recipient interprets the agreement of these values to mean the data is authentic and has integrity – that is, it originated from the other party which knows the shared key, and has not been altered in transit. This corresponds to Figure 9.8(a).
9.6.4 Data integrity using an MDC and an authentic channel
The use of a secret key is not essential in order to provide data integrity. It may be eliminated by hashing a message and protecting the authenticity of the hash via an authentic (but not necessarily private) channel. The originator computes a hash-code using an MDC over the message data, transmits the data to a recipient over an unsecured channel, and transmits the hash-code over an independent channel known to provide data origin authentication. Such authentic channels may include telephone (authenticity through voice recognition), any data medium (e.g., floppy disk, piece of paper) stored in a trusted place (e.g., locked safe), or publication over any difficult-to-forge public medium (e.g., daily newspaper). The recipient independently hashes the received data, and compares the hash-code to that received. If these values agree, the recipient accepts the data as having integrity. This corresponds to Figure 9.8(c).
Example applications include virus protection of software, and distribution of software or public keys via untrusted networks. For virus checking of computer source or object code, this technique is preferable to one resulting in encrypted text. A common example of combining an MDC with an authentic channel to provide data integrity is digital signature schemes such as RSA, which typically involve the use of MDCs, with the asymmetric signature providing the authentic channel.
9.6.5 Data integrity combined with encryption
Whereas digital signatures provide assurances regarding both integrity and authentication, in general, encryption alone provides neither. This issue is first examined, and then the question of how hash functions may be employed in conjunction with encryption to provide data integrity.
(i) Encryption alone does not guarantee data integrity
A common misconception is that encryption provides data origin authentication and data integrity, under the argument that if a message is decrypted with a key shared only with party A, and if the decrypted message is meaningful, then it must have originated from A. Here “meaningful” means the message contains sufficient redundancy or meets some other a priori expectation. While the intuition is that an attacker must know the secret key in order to manipulate messages, this is not always true. In some cases he may be able to choose the plaintext message, while in other cases he may be able to effectively manipulate
§9.6 Data integrity and message authentication |
365 |
plaintext despite not being able to control its specific content. The extent to which encrypted messages can be manipulated undetectably depends on many factors, as illustrated by the following examples.
9.81 Example (re-ordering ECB blocks) The ciphertext blocks of any block cipher used only in ECB mode are subject to re-ordering.
9.82Example (encryption of random data) If the plaintext corresponding to a given ciphertext contains no redundancy (e.g., a random key), then all attempted decryptions thereof are
meaningful, and data integrity cannot be verified. Thus, some form of redundancy is always required to allow verification of integrity; moreover, to facilitate verification in practice, explicit redundancy verifiable by automated means is required.
9.83Example (bit manipulations in additive stream ciphers) Despite the fact that the one-time pad offers unconditional secrecy, an attacker can change any single bit of plaintext by modifying the corresponding bit of ciphertext. For known-plaintext attacks, this allows an attacker to substitute selected segments of plaintext by plaintext of his own choosing. An
example target bit is the high-order bit in a numeric field known to represent a dollar value. Similar comments apply to any additive stream cipher, including the OFB mode of any block cipher.
9.84Example (bit manipulation in DES ciphertext blocks) Several standard modes of operation for any block cipher are subject to selective bit manipulation. Modifying the last ciphertext block in a CFB chain is undetectable. A ciphertext block in CFB mode which yields random noise upon decryption is an indication of possible selective bit-manipulation of the
preceding ciphertext block. A ciphertext block in CBC mode which yields random noise upon decryption is an indication of possible selective bit-manipulation of the following ciphertext block. For further discussion regarding error extension in standard modes of operation, see §7.2.2.
(ii) Data integrity using encryption and an MDC
If both confidentiality and integrity are required, then the following data integrity technique employing an m-bit MDC h may be used. The originator of a message x computes a hash value H = h(x) over the message, appends it to the data, and encrypts the augmented message using a symmetric encryption algorithm E with shared key k, producing ciphertext
C = Ek(x || h(x)) |
(9.2) |
(Note that this differs subtlely from enciphering the message and the hash separately as (Ek(x),Ek(h(x))), which e.g. using CBC requires two IVs.) This is transmitted to a recipient, who determines (e.g., by a plaintext identifier field) which key to use for decryption, and separates the recovered data x from the recovered hash H . The recipient then independently computes the hash h(x ) of the received data x , and compares this to the recovered hash H . If these agree, the recovered data is accepted as both being authentic and having integrity. This corresponds to Figure 9.8(b).
The intention is that the encryption protects the appended hash, and that it be infeasible for an attacker without the encryption key to alter the message without disrupting the correspondence between the decrypted plaintext and the recovered MDC. The properties required of the MDC here may be notably weaker, in general, than for an MDC used in conjunction with, say, digital signatures. Here the requirement, effectively a joint condition on the MDC and encryption algorithm, is that it not be feasible for an adversary to manipulate
366 |
Ch. 9 Hash Functions and Data Integrity |
or create new ciphertext blocks so as to produce a new ciphertext C which upon decryption will yield plaintext blocks having the same MDC as that recovered, with probability significantly greater than 1 in 2m.
9.85Remark (separation of integrity and privacy) While this approach appears to separate privacy and data integrity from a functional viewpoint, the two are not independent with respect to security. The security of the integrity mechanism is, at most, that of the encryption algorithm regardless of the strength of the MDC (consider exhaustive search of the encryption key). Thought should, therefore, be given to the relative strengths of the components.
9.86Remark (vulnerability to known-plaintext attack) In environments where known-plain- text attacks are possible, the technique of equation (9.2) should not be used in conjunction with additive stream ciphers unless additional integrity techniques are used. In this scenario, an attacker can recover the key stream, then make plaintext changes, recompute a new MDC, and re-encrypt the modified message. Note this attack compromises the manner in which the MDC is used, rather than the MDC or encryption algorithm directly.
If confidentiality is not essential other than to support the requirement of integrity, an apparent option is to encrypt only either the message x or the MDC h(x). Neither approach is common, for reasons including Remark 9.85, and the general undesirability to utilize encryption primitives in systems requiring only integrity or authentication services. The following further comments apply:
1.encrypting the hash-code only: (x, Ek(h(x)))
Applying the key to the hash-value only (cf. Example 9.65) results in a property (typical for public-key signatures but) atypical for MACs: pairs of inputs x,x with collid-
ing outputs (MAC-values here) can be verifiably pre-determined without knowledge of k. Thus h must be collision-resistant. Other issues include: pairs of inputs having the same MAC-value under one key also do under other keys; if the blocklength of the cipher Ek is less than the bitlength m of the hash-value, splitting the latter across encryption blocks may weaken security; k must be reserved exclusively for this integrity function (otherwise chosen-text attacks on encryption allow selective MAC forgery); and Ek must not be an additive stream cipher (see Remark 9.86).
2.encrypting the plaintext only: (Ek(x), h(x))
This offers little computational savings over encrypting both message and hash (except for very short messages) and, as above, h(x) must be collision-resistant and thus
twice the typical MAC bitlength. Correct guesses of the plaintext xmay be confirmed (candidate values x for x can be checked by comparing h(x ) to h(x)).
(iii)Data integrity using encryption and a MAC
It is sometimes suggested to use a MAC rather than the MDC in the mechanism of equation (9.2) on page 365. In this case, a MAC algorithm hk replaces the MDC h, and rather than C = Ek(x || h(x)), the message sent is
C = Ek(x || hk (x)) |
(9.3) |
The use of a MAC here offers the advantage (over an MDC) that should the encryption algorithm be defeated, the MAC still provides integrity. A drawback is the requirement of managing both an encryption key and a MAC key. Care must be exercised to ensure that dependencies between the MAC and encryption algorithms do not lead to security weaknesses, and as a general recommendation these algorithms should be independent (see Example 9.88).
§9.6 Data integrity and message authentication |
367 |
9.87Remark (precluding exhaustive MAC search) Encryption of the MAC-value in equation (9.3) precludes an exhaustive key search attack on the MAC key.
Two alternatives here include encrypting the plaintext first and then computing a MAC over the ciphertext, and encrypting the message and MAC separately. These are discussed in turn.
1.computing a MAC over the ciphertext: (Ek(x), hk (Ek(x))).
This allows message authentication without knowledge of the plaintext x (or ciphertext key). However, as the message authentication is on the ciphertext rather than the plaintext directly, there are no guarantees that the party creating the MAC knew the plaintext x. The recipient, therefore, must be careful about conclusions drawn – for
example, if Ek is public-key encryption, the originator of x may be independent of the party sharing the key k with the recipient.
2.separate encryption and MAC: (Ek(x), hk (x)).
This alternative requires that neither the encryption nor the MAC algorithm compromises the objectives of the other. In particular, in this case an additional requirement
on the algorithm is that the MAC on x must not compromise the confidentiality of x (cf. Definition 9.7). Keys (k,k ) should also be independent here, e.g., to pre-
clude exhaustive search on the weaker algorithm compromising the other (cf. Example 9.88). If k and k are not independent, exhaustive key search is theoretically
possible even without known plaintext.
(iv)Data integrity using encryption – examples
9.88Example (improper combination of CBC-MAC and CBC encryption) Consider using the
data integrity mechanism of equation (9.3) with Ek being CBC-encryption with key k and initialization vector IV , hk (x) being CBC-MAC with k and IV , and k = k , IV = IV . The data x = x1x2 ...xt can then be processed in a single CBC pass, since the CBC-MAC is equal to the last ciphertext block ct = Ek(ct−1 xt), and the last data block is xt+1 = ct, yielding final ciphertext block ct+1 = Ek(ct xt+1) = Ek(0). The encrypted MAC is thus independent of both plaintext and ciphertext, rendering the integrity mechanism completely
insecure. Care should thus be taken in combining a MAC with an encryption scheme. In general, it is recommended that distinct (and ideally, independent) keys be used. In some cases, one key may be derived from the other by a simple technique; a common suggestion for DES keys is complementation of every other nibble. However, arguments favoring independent keys include the danger of encryption algorithm weaknesses compromising authentication (or vice-versa), and differences between authentication and encryption keys
with respect to key management life cycle. See also Remark 13.32. |
|
An efficiency drawback in using distinct keys for secrecy and integrity is the cost of two separate passes over the data. Example 9.89 illustrates a proposed data integrity mechanism (which appeared in a preliminary draft of U.S. Federal Standard 1026) which attempts this by using an essentially zero-cost linear checksum; it is, however, insecure.
9.89Example (CBC encryption with XOR checksum – CBCC) Consider using the data integrity mechanism of equation (9.2) with Ek being CBC-encryption with key k, x = x1x2 ...
xt a message of t blocks, and as MDC function the simple XOR of all plaintext blocks,
i=t
h(x) = i=1 xi. The quantity M = h(x) which serves as MDC then becomes plaintext block xt+1. The resulting ciphertext blocks using CBC encryption with c0 = IV are ci = Ek(xi ci−1), 1 ≤ i ≤ t + 1. In the absence of manipulation, the recovered plaintext is xi = ci−1 Dk(ci). To see that this scheme is insecure as an integrity mechanism, let ci denote the actual ciphertext blocks received by a recipient, resulting from possibly

368 |
Ch. 9 Hash Functions and Data Integrity |
manipulated blocks ci, and let xi denote the plaintext recovered by the recipient by CBC decryption with the proper IV. The MDC computed over the recovered plaintext blocks is then
|
i=t |
i=t |
|
|
|
|
|
i=t−1 |
i=t |
|
|
|
|
|
|
|
|
|
|
|
|
M = h(x ) = |
xi |
= |
(ci−1 Dk(ci)) = IV ( |
ci) ( Dk(ci) ) |
|
|||||
|
i=1 |
i=1 |
|
|
|
|
|
i=1 |
i=1 |
|
M is compared for equality with x |
|
(= c Dk |
(c |
)) as a check for data integrity, or |
||||||
equivalently, that S = M x |
t+1 |
t |
|
t+1 |
|
|
|
|||
= 0. By construction, S = 0 if there is no manipula- |
||||||||||
|
|
t+1 |
|
= xi). Moreover, the sum S is invariant under any |
||||||
tion (i.e., if c = ci, which implies x |
||||||||||
i |
|
|
i |
|
|
|
|
|
|
|
permutation of the values c |
,1 ≤ i ≤ t (since D |
k |
(c |
) appears as a term in S, but c |
t+1 |
|||||
|
i |
|
|
|
|
t+1 |
|
|
||
does not, ct+1 must be excluded from the permutable set). Thus, any of the first t ciphertext blocks can be permuted without affecting the successful verification of the MDC. Further-
more, insertion into the ciphertext stream of any random block cj twice, or any set of such |
|
pairs, will cancel itself out in the sum S, and thus also cannot be detected. |
|
9.90Example (CBC encryption with mod 2n −1 checksum) Consider as an alternative to Example 9.89 the simple MDC function h(x) = ti=1 xi, the sum of plaintext blocks as n-bit integers with wrap-around carry (add overflow bits back into units bit), i.e., the sum modulo 2n − 1; consider n = 64 for ciphers of blocklength 64. The sum S from Example 9.89 in
this case involves both XOR and addition modulo 2n −1; both permutations of ciphertext blocks and insertions of pairs of identical random blocks are now detected. (This technique should not, however, be used in environments subject to chosen-plaintext attack.)
9.91Example (PCBC encryption with mod 2n checksum) A non-standard, non-self-synchron- izing mode of DES known as plaintext-ciphertext block chaining (PCBC) is defined as follows, for i ≥ 0 and plaintext x = x1x2 ...xt: ci+1 = Ek(xi+1 Gi) where G0 = IV , Gi = g(xi,ci) for i ≥ 1, and g a simple function such as g(xi,ci) = (xi + ci) mod 264. A one-pass technique providing both encryption and integrity, which exploits the errorpropagation property of this mode, is as follows. Append an additional plaintext block to provide redundancy, e.g., xt+1 = IV (alternatively: a fixed constant or x1). Encrypt all blocks of the augmented plaintext using PCBC encryption as defined above. The quantity
ct+1 =Ek(xt+1 g(xt,ct)) serves as MAC. Upon decipherment of ct+1, the receiver accepts the message as having integrity if the expected redundancy is evident in the recovered block xt+1. (To avoid a known-plaintext attack, the function g in PCBC should not be a simple XOR for this integrity application.)
9.7 Advanced attacks on hash functions
A deeper understanding of hash function security can be obtained through consideration of various general attack strategies. The resistance of a particular hash function to known general attacks provides a (partial) measure of security. A selection of prominent attack strategies is presented in this section, with the intention of providing an introduction sufficient to establish that designing (good) cryptographic hash functions is not an easily mastered art. Many other attack methods and variations exist; some are general methods, while others rely on peculiar properties of the internal workings of specific hash functions.

§9.7 Advanced attacks on hash functions |
369 |
9.7.1 Birthday attacks
Algorithm-independent attacks are those which can be applied to any hash function, treating it as a black-box whose only significant characteristics are the output bitlength n (and MAC key bitlength for MACs), and the running time for one hash operation. It is typically assumed the hash output approximates a uniform random variable. Attacks falling under this category include those based on hash-result bitsize (page 336); exhaustive MAC key search (page 336); and birthday attacks on hash functions (including memoryless variations) as discussed below.
(i) Yuval’s birthday attack on hash functions
Yuval’s birthday attack was one of the first (and perhaps the most well-known) of many cryptographic applications of the birthday paradox arising from the classical occupancy
distribution (§2.1.5): when drawing elements randomly, with replacement, from a set of
√
N elements, with high probability a repeated element will be encountered after O( N) selections. Such attacks are among those called square-root attacks.
The relevance to hash functions is that it is easier to find collisions for a one-way hash function than to find pre-images or second preimages of specific hash-values. As a result, signature schemes which employ one-way hash functions may be vulnerable to Yuval’s attack outlined below. The attack is applicable to all unkeyed hash functions (cf. Fact 9.33), with running time O(2m/2) varying with the bitlength m of the hash-value.
9.92Algorithm Yuval’s birthday attack
INPUT: legitimate message x1; fraudulent message x2; m-bit one-way hash function h.
OUTPUT: x1, x2 resulting from minor modifications of x1, x2 with h(x1) = h(x2) (thus a signature on x1 serves as a valid signature on x2).
1.Generate t = 2m/2 minor modifications x1 of x1.
2.Hash each such modified message, and store the hash-values (grouped with corresponding message) such that they can be subsequently searched on hash-value. (This can done in O(t) total time using conventional hashing.)
3.Generate minor modifications x2 of x2, computing h(x2) for each and checking for matches with any x1 above; continue until a match is found. (Each table lookup will require constant time; a match can be expected after about t candidates x2.)
9.93Remark (application of birthday attack) The idea of this attack can be used by a dishon-
est signer who provides to an unsuspecting party his signature on x1 and later repudiates signing that message, claiming instead that the message signed was x2; or by a dishonest verifier, who is able to convince an unsuspecting party to sign a prepared message x1, and later claim that party’s signature on x2. This remark generalizes to other schemes in which the hash of a message is taken to represent the message itself.
Regarding practicality, the collisions produced by the birthday attack are “real” (vs. pseudo-collisions or compression function collisions), and moreover of direct practical consequence when messages are constructed to be meaningful. The latter may often be done as follows: alter inputs via individual minor modifications which create semantically equivalent messages (e.g., substituting tab characters in text files for spaces, unprintable characters for each other, etc.). For 128-bit hash functions, 64 such potential modification points are
370 |
Ch. 9 Hash Functions and Data Integrity |
required to allow 264 variations. The attack then requires O(264) time (feasible with extreme parallelization); and while it requires space for O(264) messages (which is impractical), the memory requirement can be addressed as discussed below.
(ii) Memoryless variation of birthday attack
To remove the memory requirement of Algorithm 9.92, a deterministic mapping may be used which approximates a random walk through the hash-value space. By the birthday paradox, in a random walk through a space of 2m points, one expects to encounter some point a second time (i.e., obtain a collision) after O(2m/2) steps, after which the walk will repeat its previous path (and begin to cycle). General memoryless cycle-finding techniques may then be used to find this collision. (Here memoryless means requiring negligible memory, rather than in the stochastic sense.) These include Floyd’s cycle-finding algorithm (§3.2.2) and improvements to it.
Following Algorithm 9.92, let g be a function such that g(x1,H) = x1 is a minor modification, determined by the hash-value H, of message x1 (each bit of H might define whether or not to modify x1 at a pre-determined modification point). If x1 is fixed, then g essentially maps a hash-result to a message and it is convenient to write gx1 (H) = x1. Moreover, let g be injective so that distinct hashes H result in distinct x1. Then, with fixed messages x1, x2, and using some easily distinguishable property (e.g., parity) which splits the space of hash-values into two roughly equal-sized subsets, define a function r mapping hash-results to hash-results by:
h(gx1 |
(H)) |
if H is even |
|
r(H) = h(gx2 |
(H)) |
if H is odd |
(9.4) |
The memoryless collision search technique (see above) is then used to find two inputs to r which map to the same output (i.e., collide). If h behaves statistically as a random mapping then, with probability 0.5, the parity will differ in H and H for the colliding inputs, in which case without loss of generality h(gx1 (H)) = h(gx2 (H )). This yields a colliding pair of variations x1 = gx1 (H), x2 = gx2 (H ) of distinct messages x1, x2, respectively, such that h(x1) = h(x2), as per the output of Algorithm 9.92.
(iii) Illustrative application to MD5
Actual application of the above generic attack to a specific hash function raises additional technicalities. To illustrate how these may be addressed, such application is now examined, with assumptions and choices made for exposition only. Let h be an iterated hash function processing messages in 512-bit blocks and producing 128-bit hashes (e.g., MD5, RIPEMD128). To minimize computational expense, restrict r (effectively g and h) in equation (9.4) to single 512-bit blocks of xi, such that each iteration of r involves only the compression function f on inputs one message block and the current chaining variable.
Let the legitimate message input x1 consist of s 512-bit blocks (s ≥ 1, prior to MDstrengthening). Create a fraudulent message x2 of equal bitlength. Allow x2 to differ from x1 up to and including the jth block, for any fixed j ≤ s−1. Use the (j + 1)st block of xi, denoted Bi (i = 1,2), as a matching/replacement block, to be replaced by the 512-bit blocks resulting from the collision search. Set all blocks in x2 subsequent to Bi identically equal to those in x1; xi will then differ from xi only in the single block (j + 1). For maximum freedom in the construction of x2, choose j = s − 1. Let c1, c2 be the respective 128-bit intermediate results (chaining variables) after the iterated hash operates on the first j blocks of x1, x2. Compression function f maps (128 + 512 =) 640-bit inputs to 128-bit outputs. Since the chaining variables depend on xi, gxi (= g) may be defined independent of xi here (cf. equation (9.4)); assume both entire blocks Bi may be replaced without practical

§9.7 Advanced attacks on hash functions |
371 |
implication. Let g(H) = B denote an injective mapping from the space of 128-bit hashvalues to the space of 512-bit potential replacement blocks, defined as follows: map each two-bit segment of H to one of four 8-bit values in the replacement block B. (A practical motivation for this is that if xi is an ASCII message to be printed, and the four 8-bit values are selected to represent non-printable characters, then upon printing, the resulting blocks B are all indistinguishable, leaving no evidence of adversarial manipulation.)
The collision-finding function r for this specific example (corresponding to the generic equation (9.4)) is then:
f(c1 |
, g(H)) |
if H is even |
r(H) = f(c2 |
, g(H)) |
if H is odd |
Collisions for MD5 (and similar hash functions) can thus be found in O(264) operations and without significant storage requirements.
9.7.2 Pseudo-collisions and compression function attacks
The exhaustive or brute force methods discussed in §9.3.4, producing preimages, 2nd-pre- images, and collisions for hash functions, are always theoretically possible. They are not considered true “attacks” unless the number of operations required is significantly less than both the strength conjectured by the hash function designer and that of hash functions of similar parameters with ideal strength. An attack requiring such a reduced number of operations is informally said to break the hash function, whether or not this computational effort is feasible in practice. Any attack method which demonstrates that conjectured properties do not hold must be taken seriously; when this occurs, one must admit the possibility of additional weaknesses.
In addition to considering the complexity of finding (ordinary) preimages and collisions, it is common to examine the feasibility of attacks on slightly modified versions of the hash function in question, for reasons explained below. The most common case is examination of the difficulty of finding preimages or collisions if one allows free choice of IVs. Attacks on hash functions with unconstrained IVs dictate upper bounds on the security of the actual algorithms. Vulnerabilities found, while not direct weaknesses in the overall hash function, are nonetheless considered certificational weaknesses and cast suspicion on overall security. In some cases, restricted attacks can be extended to full attacks by standard techniques.
Table 9.11 lists the most commonly examined variations, including pseudo-collisions
– collisions allowing different IVs for the different message inputs. In contrast to preimages and collisions, pseudo-preimages and pseudo-collisions are of limited direct practical significance.
9.94Note (alternate names for collision and preimage attacks) Alternate names for those in Table 9.11 are as follows: preimage or 2nd-preimage ≡ target attack; pseudo-preimage ≡ free-start target attack; collision (fixed IV) ≡ collision attack; collision (random IV) ≡ semi-free-start collision attack; pseudo-collision ≡ free-start collision attack.
9.95Note (relative difficulty of attacks) Finding a collision can be no harder than finding a 2ndpreimage. Similarly, finding a pseudo-collision can be no harder than finding (two distinct) pseudo-preimages.
372 |
|
|
|
|
|
|
|
Ch. 9 Hash Functions and Data Integrity |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
↓Type of attack |
|
V |
V |
x |
x |
y |
Find ... |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
preimage |
|
V0 |
— |
* |
— |
y0 |
x: h(V0,x) = y0 |
|
||
|
pseudo-preimage |
|
* |
— |
* |
— |
y0 |
x,V : h(V,x) = y0 |
|
|
|
|
2nd-preimage |
|
V0 |
V0 |
x0 |
* |
h(V0,x0) |
x : h(V0,x0) = h(V0,x ) |
|
|
|
|
collision (fixed IV) |
|
V |
0 |
V |
* |
* |
— |
x,x : |
|
|
|
|
|
|
0 |
|
|
|
h(V0,x) = h(V0,x ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
collision (random IV) |
|
* |
V |
* |
* |
— |
x,x ,V : |
|
|
|
|
|
|
|
|
|
|
|
|
h(V,x) = h(V,x ) |
|
|
|
pseudo-collision |
|
* |
* |
* |
* |
— |
x,x ,V,V : |
|
|
|
|
|
|
|
|
|
|
|
|
h(V,x) = h(V ,x ) |
|
|
Table 9.11: Definition of preimage and collision attacks. V and V denote (potentially different) IVs used for MDC h applied to inputs x and x , respectively; V0 denotes the IV pre-specified in the definition of h, x0 a pre-specified target input, and y = y0 a pre-specified target output. * Denotes
IVs or inputs which may be freely chosen by an attacker; h(V0, x0) denotes the hash-code resulting from applying h with fixed IV V = V0 to input x = x0. — Means not applicable.
9.96Example (trivial collisions for random IVs) If free choice of IV is allowed, then trivial pseudo-collisions can be found by deleting leading blocks from a target message. For exam-
ple, for an iterated hash (cf. equation (9.1) on page 333), h(IV,x1x2) = f(f(IV,x1),x2). Thus, for IV = f(IV,x1), h(IV ,x2) = h(IV,x1x2) yields a pseudo-collision of h, independent of the strength of f. (MD-strengthening as per Algorithm 9.26 precludes this.)
Another common analysis technique is to consider the strength of weakened variants of an algorithm, or attack specific subcomponents, akin to cryptanalyzing an 8-round version of DES in place of the full 16 rounds.
9.97Definition An attack on the compression function of an iterated hash function is any attack as per Table 9.11 with f(Hi−1,xi) replacing h(V0,x) – the compression function f in place of hash function h, chaining variable Hi−1 in place of initializing value V , and a single input block xi in place of the arbitrary-length message x.
An attack on a compression function focuses on one fixed step i of the iterative function of equation (9.1). The entire message consists of a single block xi = x (without MD-strengthening), and the hash output is taken to be the compression function output so h(x) = Hi. The importance of such attacks arises from the following.
9.98Note (compression function vs. hash function attacks) Any of the six attacks of Table 9.11 which is found for the compression function of an iterated hash can be extended to a similar attack of roughly equal complexity on the overall hash. An iterated hash function is thus in this regard at most as strong as its compression function. (However note, for example, an overall pseudo-collision is not always of practical concern, since most hash functions specify a fixed IV.)
For example, consider a message x = x1x2 ...xt. Suppose a successful 2nd-preimage
attack on compression function f yields a 2nd-preimage x |
=x1 |
such that f(IV,x |
) = |
|||
f(IV,x ). Then, x = x |
|
1 |
|
1 |
|
|
x |
...x is a preimage of h(x). |
|
|
|
||
1 |
1 |
2 |
t |
|
|
|
More positively, if MD-strengthening is used, the strength of an iterated hash with respect to the attacks of Table 9.11 is the same as that of its compression function (cf.

§9.7 Advanced attacks on hash functions |
373 |
Fact 9.24). However, an iterated hash may certainly be weaker than its compression function (e.g., Example 9.96; Fact 9.37).
In summary, a compression function secure against preimage, 2nd-preimage, and collision (fixed IV) attacks is necessary and sometimes, but not always, sufficient for a secure iterated hash; and security against the other (i.e., free-start) attacks of Table 9.11 is desirable, but not always necessary for a secure hash function in practice. For this reason, compression functions are analyzed in isolation, and attacks on compression functions as per Definition 9.97 are considered. A further result motivating the study of pseudo-preimages is the following.
9.99Fact (pseudo-preimages yielding preimages) If the compression function f of an n-bit iterated hash function h does not have ideal computational security (2n) against pseudopreimage attacks, then preimages for h can be found in fewer than 2n operations (cf. §9.3.4, Table 9.2). This result is true even if h has MD-strengthening.
Justification. The attack requires messages of 3 or more blocks, with 2 or more uncon-
strained to allow a meet-in-the-middle attack (page 374). If pseudo-preimages can be found in 2s operations, then 2(n+s)/2 forward points and 2(n−s)/2 backward points are employed (fewer backward points are used since they are more costly). Preimages can thus be found in 2 · 2(n+s)/2 operations.
9.7.3Chaining attacks
Chaining attacks are those which are based on the iterative nature of hash functions and, in particular, the use of chaining variables. These focus on the compression function f rather than the overall hash function h, and may be further classified as below. An example for context is first given.
9.100 Example (chaining attack) Consider a (candidate) collision resistant iterative hash function h producing a 128-bit hash-result, with a compression function f taking as inputs a 512-bit message block xi and 128-bit chaining variable Hi (H0 = IV ) and producing output Hi+1 = f(Hi,xi). For a fixed 10-block message x (640 bytes), consider H = h(x). Suppose one picks any one of the 10 blocks, and wishes to replace it with another block without affecting the hash H. If h behaves like a random mapping, the number of such 512-bit blocks is approximately 2512/2128 = 2384. Any efficient method for finding any one of these 2384 blocks distinct from the original constitutes an attack on h. The challenge is that such blocks are a sparse subset of all possible blocks, about 1 in 2128.
(i) Correcting-block chaining attacks
Using the example above for context, one could attempt to (totally) replace a message x with a new message x , such that h(x) = h(x ), by using a single unconstrained “correcting” block in x , designated ahead of time, to be determined later such that it produces a chaining value which results in the overall hash being equal to target value h(x). Such a correcting block attack can be used to find both preimages and collisions. If the unconstrained block is the first (last) block in the message, it is called a correcting first (last) block attack. These attacks may be precluded by requiring per-block redundancy, but this results in an undesirable bandwidth penalty. Example 9.101 illustrates a correcting first block attack. The extension of Yuval’s birthday attack (page 369), with message alterations restricted to the last block of candidate messages, resembles a correcting last block attack applied simultaneously to two messages, seeking a (birthday) collision rather than a fixed overall target hash-value.

374 Ch. 9 Hash Functions and Data Integrity
9.101 Example (correcting block attack on CBC cipher mode) The CBC mode of encryption with non-secret key (H0 = IV ; Hi = Ek(Hi−1 xi)) is unsuitable as an MDC algorithm, because it fails to be one-way – the compression function is reversible when the encryption key is known. A message x , of unconstrained length (say t blocks) can be constructed to have any specified target hash-value H as follows. Let x2,...xt be t − 1 blocks chosen
freely. Set Ht ← H, then for i from tto 1 compute Hi−1 ← Dk(Hi) xi. Finally, compute x1 ← Dk(H1) IV . Then, for x = x1x2 ...xt, h(x ) = H and all but block x1 (which will appear random) can be freely chosen by an adversary; even this minor drawback can
be partially addressed by a meet-in-the-middle strategy (see below). Analogous remarks apply to the CFB mode.
(ii) Meet-in-the-middle chaining attacks
These are birthday attacks similar to Yuval’s (and which can be made essentially memoryless) but which seek collisions on intermediate results (i.e., chaining variables) rather than the overall hash-result. When applicable, they allow (unlike Yuval’s attack) one to find a message with a pre-specified hash-result, for either a 2nd-preimage or a collision. An attack point is identified between blocks of a candidate (fraudulent) message. Variations of the blocks preceding and succeeding this point are generated. The variations are hashed forward from the algorithm-specified IV (computing Hi = f(Hi−1,xi) as usual) and backward from the target final hash-result (computing Hi = f−1(Hi+1,xi+1) for some Hi+1, xi+1, ideally for xi+1 chosen by the adversary), seeking a collision in the chaining variable Hi at the attack point. For the attack to work, the attacker must be able to efficiently go backwards through the chain (certainly moreso than by brute force – e.g., see Example 9.102), i.e., invert the compression function in the following manner: given a value Hi+1, find a pair (Hi,xi+1) such that f(Hi,xi+1) = Hi+1.
9.102 Example (meet-in-the-middle attack on invertible key chaining modes) Chaining modes which allow easily derived stage keys result in reversible compression functions unsuitable for use in MDCs due to lack of one-wayness (cf. Example 9.101). An example of such invertible key chaining methods is Bitzer’s scheme: H0 = IV , Hi = f(Hi−1,xi) = Eki (Hi−1) where ki = xi s(Hi−1) and s(Hi−1) is a function mapping chaining variables to the key space. For exposition, let s be the identity function. This compression function is unsuitable because it falls to a meet-in-the-middle attack as outlined above. The ability to move backwards through chaining variables, as required by such an attack, is possible here with the chaining variable Hi computed from Hi+1 as follows. Choose a fixed value ki+1 ← k, compute Hi ← Dk(Hi+1), then choose as message block xi+1 ← k Hi.
(iii) Fixed-point chaining attacks
A fixed point of a compression function is a pair (Hi−1,xi) such that f(Hi−1,xi) = Hi−1. For such a pair of message block and chaining value, the overall hash on a message is unchanged upon insertion of an arbitrary number of identical blocks xi at the chain point at which that chaining value arises. Such attacks are thus of concern if it can be arranged that the chaining variable has a value for which a fixed point is known. This includes the following cases: if fixed points can be found and it can be easily arranged that the chaining variable take on a specific value; or if for arbitrary chaining values Hi−1, blocks xi can be found which result in fixed-points. Fixed points allow 2nd-preimages and collisions to be produced; their effect can be countered by inclusion of a trailing length-block (Algorithm 9.26).

§9.7 Advanced attacks on hash functions |
375 |
(iv) Differential chaining attacks
Differential cryptanalysis has proven to be a powerful tool for the cryptanalysis of not only block ciphers but also of hash functions (including MACs). For multi-round block ciphers this attack method examines input differences (XORs) to round functions and the corresponding output differences, searching for statistical anomalies. For hash functions, the examination is of input differences to compression functions and the corresponding output differences; a collision corresponds to an output difference of zero.
9.7.4 Attacks based on properties of underlying cipher
The implications of certain properties of block ciphers, which may be of no practical concern when used for encryption, must be carefully examined when such ciphers are used to construct iterated hash functions. The general danger is that such properties may facilitate adversarial manipulation of compression function inputs so as to allow prediction or greater control of outputs or relations between outputs of successive iterations. Included among block cipher properties of possible concern are the following (cf. Chapter 7):
1.complementation property: y = Ek(x) y = Ek(x), where x denotes bitwise complement. This makes it trivial to find key-message pairs of block cipher inputs
whose outputs differ in a pre-determined manner. For example, for such a block ci-
pher E, the compression function f(Hi−1,xi) = EHi−1 xi (xi) xi (a linear transformation of the Matyas-Meyer-Oseas function) produces the same output for xi and its bitwise complement xi.
2.weak keys: Ek(Ek(x)) = x (for all x). This property of involution of the block cipher may allow an adversary to easily create a two-step fixed point of the compression function f in the case that message blocks xi have direct influence on the block cipher key input (e.g., if f = Exi (Hi−1), insert 2 blocks xi containing a weak key). The threat is similar for semi-weak keys, where Ek (Ek(x)) = x.
3.fixed points: Ek(x) = x. Block cipher fixed points may facilitate fixed-point attacks if an adversary can control the block cipher key input. For example, for the Davies-
Meyer compression function f(Hi−1,xi) = Exi (Hi−1) Hi−1, if Hi−1 is a fixed point of the block cipher for key xi (i.e., Exi (Hi−1) = Hi−1), then this yields a predictable compression function output f(Hi−1,xi) = 0.
4.key collisions: Ek(x) = Ek (x). These may allow compression function collisions.
Although they may serve as distinguishing metrics, attacks which appear purely certificational in nature should be noted separately from others; for example, fixed point attacks appear to be of limited practical consequence.
9.103 Example (DES-based hash functions) Consider DES as the block cipher in question (see §7.4). DES has the complementation property; has 4 weak keys and 6 pairs of semi-weak keys (each with bit 2 equal to bit 3); each weak key has 232 fixed points (thus a random plaintext is a fixed point of some weak key with probability 2−30), as do 4 of the semiweak keys; and key collisions can be found in 232 operations. The security implications of these properties must be taken into account in the design of any DES-based hash function. Concerns regarding both weak keys and the complementation property can be eliminated by forcing key bits 2 and 3 to be 10 or 01 within the compression function.

376 |
Ch. 9 Hash Functions and Data Integrity |
9.8 Notes and further references
§9.1
The definitive reference for cryptographic hash functions, and an invaluable source for the material in this chapter (including many otherwise unattributed results), is the comprehensive treatment of Preneel [1003, 1004]; see also the surveys of Preneel [1002] and Preneel, Govaerts, and Vandewalle [1006]. Davies and Price [308] also provide a solid treatment of message authentication and data integrity. An extensive treatment of conventional hashing, including historical discussion tracing origins back to IBM in 1953, is given by Knuth [693, p.506-549]. Independent of cryptographic application, universal classes of hash functions were introduced by Carter and Wegman [234] in the late 1970s, the idea being to find a class of hash functions such that for every pair of inputs, the probability was low that a randomly chosen function from the class resulted in that pair colliding. Shortly thereafter, Wegman and Carter [1234] noted the cryptographic utility of these hash functions, when combined with secret keys, for (unconditionally secure) message authentication tag systems; they formalized this concept, earlier considered by Gilbert, MacWilliams, and Sloane [454] (predating the concept of digital signatures) who attribute the problem to Simmons. Simmons ([1138],[1144]; see also Chapter 10 of Stinson [1178]) independently developed a general theory of unconditionally secure message authentication schemes and the subject of authentication codes (see also §9.5 below).
Rabin [1022, 1023] first suggested employing a one-way hash function (constructed by using successive message blocks to key an iterated block encryption) in conjunction with a one-time signature scheme and later in a public-key signature scheme; Rabin essentially noted the requirements of 2nd-preimage resistance and collision resistance. Merkle [850] explored further uses of one-way hash functions for authentication, including the idea of tree authentication [852] for both one-time signatures and authentication of public files.
§9.2
Merkle [850] (partially published as [853]) was the first to give a substantial (informal) definition of one-way hash functions in 1979, specifying the properties of preimage and 2ndpreimage resistance. Foreshadowing UOWHFs (see below), he suggested countering the effect of Remark 9.36 by using slightly different hash functions h over time; Merkle [850, p.16-18] also proposed a public key distribution method based on a one-way hash function (effectively used as a one-way pseudo-permutation) and the birthday paradox, in a precursor to his “puzzle system” (see page 537). The first formal definition of a CRHF was given in 1988 by Damg˚ard [295] (an informal definition was later given by Merkle [855, 854]; see also [853]), who was first to explore collision resistant hash functions in a complexitytheoretic setting. Working from the idea of claw-resistant pairs of trapdoor permutations due to Goldwasser, Micali, and Rivest [484], Damg˚ard defined claw-resistant families of permutations (without the trapdoor property). The term claw-resistant (originally: clawfree) originates from the pictorial representation of a functional mapping showing two distinct domain elements being mapped to the same range element under distinct functions f(i) and f(j) (colliding at z = f(i)(x) = f(j)(y)), thereby tracing out a claw.
Goldwasser et al. [484] established that the intractability of factoring suffices for the existence of claw-resistant pairs of permutations. Damg˚ard showed that the intractability of the discrete logarithm problem likewise suffices. Using several reasonably efficient numbertheoretic constructions for families of claw-resistant permutations, he gave the first provably collision resistant hash functions, under such intractability assumptions (for discrete
§9.8 Notes and further references |
377 |
logarithms, the assumption required is that taking specific discrete logarithms be difficult). Russell [1088] subsequently established that a collection of collision resistant hash functions exists if and only if there exists a collection of claw-resistant pairs of pseudo-permu- tations; a pseudo-permutation on a set is a function computationally indistinguishable from a permutation (pairs of elements demonstrating non-injectivity are hard to find). It remains open whether the existence of one-way functions suffices for the existence of collision resistant hash functions.
The definition of a one-way function (Definition 9.9) was given in the seminal paper of Diffie and Hellman [345], along with the use of the discrete exponential function modulo a prime as a candidate OWF, which they credit to Gill. The idea of providing the hashvalue of some data, to indicate prior commitment to (or knowledge of) that data, was utilized in Lamport’s one-time signature scheme (circa 1976); see page 485. The OWF of Example 9.13 was known to Matyas and Meyer circa 1979. As noted by Massey [786], the idea of one-wayness was published in 1873 by J.S. Jevons, who noted (preceding RSA by a century) that multiplying two primes is easy whereas factoring the result is not. Published work dated 1968 records the use of ciphers essentially as one-way functions (decryption was not required) in a technique to avoid storing cleartext computer account passwords in time-shared systems. These were referred to as one-way ciphers by Wilkes [1244] (p.9193 in 1968 or 1972 editions; p.147 in 1975 edition), who credits Needham with the idea and an implementation thereof. The first proposal of a non-invertible function for the same purpose appears to be that of Evans, Kantrowitz, and Weiss [375], while Purdy [1012] proposed extremely high-degree, sparse polynomials over a prime field as a class of functions which were computationally difficult to invert. Foreshadowing later research into collision resistance, Purdy also defined the degeneracy of such a function to be the maximum number of preimages than any image could have, noting that “if the degeneracy is catastrophically large there may be no security at all”.
Naor and Yung [920] introduced the cryptographic primitive known as a universal one-way hash function (UOWHF) family, and give a provably secure construction for a one-way hash function from a one-way hash function which compresses by a single bit (t + 1 to t bits); the main property of a UOWHF family is 2nd-preimage resistance as for a OWHF, but here an instance of the function is picked at random from a family of hash functions after fixing an input, as might be modeled in practice by using a random IV with a OWHF. Naor and Yung [920] also prove by construction that UOWHFs exist if and only if one-way permutations do, and show how to use UOWHFs to construct provably secure digital signature schemes assuming the existence of any one-way permutation. Building on this, Rompel [1068] showed how to construct a UOWHF family from any one-way function, and based signature schemes on such hash functions; combining this with the fact that a one-way function can be constructed from any secure signature scheme, the result is that the existence of one-way functions is necessary and sufficient for the existence of secure digital signature schemes. De Santis and Yung [318] proceed with more efficient reductions from one-way functions to UOWHFs, and show the equivalence of a number of complexity-theoretic definitions regarding collision resistance. Impagliazzo and Naor [569] give an efficient construction for a UOWHF and prove security equivalent to the subset-sum problem (an NP- hard problem whose corresponding decision problem is NP-complete); for parameters for which a random instance of subset-sum is hard, they argue that this UOWHF is secure (cf. Remark 9.12). Impagliazzo, Levin, and Luby [568] prove the existence of one-way functions is necessary and sufficient for that of secure pseudorandom generators.
Application-specific (often unprovable) hash function properties beyond collision resistance (but short of preimage resistance) may often be identified as necessary, e.g., for or-
378 |
Ch. 9 Hash Functions and Data Integrity |
dinary RSA signatures computed directly after hashing, the multiplicative RSA property dictates that for the hash function h used it be infeasible to find messages x, x1, x2 such that h(x) = h(x1) · h(x2). Anderson [27] discusses such additional requirements on hash functions. For a summary of requirements on a MAC in the special case of multi-cast authentication, see Preneel [1003]. Bellare and Rogaway [93] include discussion of issues related to the random nature of practical hash functions, and cryptographic uses thereof. Damg˚ard [295] showed that the security of a digital signature scheme which is not existentially forgeable under an adaptive chosen-message attack will not be decreased if used in conjunction with a collision-resistant hash function.
Bellare, Goldreich, and Goldwasser [88] (see also [89]) introduce the idea of incremental hashing, involving computing a hash value over data and then updating the hash-value after changing the data; the objective is that the computation required for the update be proportional to the amount of change.
§9.3
Merkle’s meta-method [854] (Algorithm 9.25) was based on ideas from his 1979 Ph.D. thesis [850]. An equivalent construction was given by Damg˚ard [296], which Gibson [450] remarks on again yielding Merkle’s method. Naor and Yung [920] give a related construction for a UOWHF. See Preneel [1003] for fundamental results (cf. Remarks 9.35 and 9.36, and Fact 9.27 on cascading hash functions which follow similar results on stream ciphers by Maurer and Massey [822]). The padding method of Algorithms 9.29 and 9.30 originated from ISO/IEC 10118-4 [608]. The basic idea of the long-message attack (Fact 9.37) is from Winternitz [1250].
§9.4
The hash function of Algorithm 9.42 and referred to as Davies-Meyer (as cited per Quisquater and Girault [1019]) has been attributed by Davies to Meyer; apparently known to Meyer and Matyas circa 1979, it was published along with Algorithm 9.41 by Matyas, Meyer, and Oseas [805]. The Miyaguchi-Preneel scheme (Algorithm 9.43) was proposed circa 1989 by Preneel [1003], and independently by Miyaguchi, Ohta, and Iwata [886]. The three single-length rate-one schemes discussed (Remark 9.44) are among 12 compression functions employing non-invertible chaining found through systematic analysis by Preneel et al. [1007] to be provably secure under black-box analysis, 8 being certificationally vulnerable to fixed-point attack nonetheless. These 12 are linear transformations on the message block and chaining variable (i.e., [x ,H ] = A[x,H] for any of the 6 invertible 2 × 2 binary matrices A) of the Matyas-Meyer-Oseas (Algorithm 9.41) and Miyaguchi-Preneel schemes; these latter two themselves are among the 4 recommended when the underlying cipher is resistant to differential cryptanalysis (e.g., DES), while Davies-Meyer is among the remaining 8 recommended otherwise (e.g., for FEAL). MDC-2 and MDC-4 are of IBM origin, proposed by Brachtl et al. [184], and reported by Meyer and Schilling [860]; details of MDC-2 are also reported by Matyas [803]. For a description of MDC-4, see Bosselaers and Preneel [178].
The DES-based hash function of Merkle [855] which is mentioned uses the meta-method and employs a compression function f mapping 119-bit input to 112-bit output in 2 DES operations, allowing 7-bit message blocks to be processed (with rate 0.055). An optimized version maps 234 bits to 128 bits in 6 DES operations, processing 106-bit message blocks (with rate 0.276); unfortunately, overheads related to “bit chopping” and the inconvenient block size are substantial in practice. This construction is provably as secure as the underlying block cipher assuming an unflawed cipher (cf. Table 9.3; Preneel [1003] shows that accounting for DES weak keys and complementation drops the rate slightly to 0.266). Win-
§9.8 Notes and further references |
379 |
ternitz [1250] considers the security of the Davies-Meyer hash under a black-box model (cf. Remark 9.45).
The search for secure double-length hash functions of rate 1 is ongoing, the goal being security better than single-length Matyas-Meyer-Oseas and approaching that of MDC-2. Quisquater and Girault [1019] proposed two functions, one (QG-original) appearing in the Abstracts of Eurocrypt’89 and a second (QG-revised) in the final proceedings altered to counter an attack of Coppersmith [276] on the first. The attack, restricted to the case of DES as underlying block cipher, uses fixed points resulting from weak keys to find collisions in 236 DES operations. A general attack of Knudsen and Lai [688], which (unfortunately) applies to a large class of double-length (i.e., 2n-bit) rate-one block-cipher-based hashes including QG-original, finds preimages in about 2n operations plus 2n storage. The systematic method used to establish this result was earlier used by Hohl et al. [560] to prove that pseudo-preimage and pseudo-collision attacks on a large class of double-length hash functions of rate 1/2 and 1, including MDC-2, are no more difficult than on the single-length rate-one Davies-Meyer hash; related results are summarized by Lai and Knudsen [727]. A second attack due to Coppersmith [276], not restricted to DES, employs 88 correcting blocks to find collisions for QG-revised in 240 steps. Another modification of QG-original, the LOKI Double Hash Function (LOKI-DBH) of Brown, Pieprzyk, and Seberry [215], appears as a general construction to offer the same security as QG-revised (provided the underlying block cipher is not LOKI).
The speeds in Table 9.5 are normalized from the timings reported by Dobbertin, Bosselaers, and Preneel [355], relative to an assembly code MD4 implementation optimized for the Pentium processor, with a throughput (90 MHz clock) of 165.7 Mbit/s (optimized C code was roughly a factor of 2 slower). See Bosselaers, Govaerts, and Vandewalle [177] for a detailed MD5 implementation discussion.
MD4 and MD5 (Algorithms 9.49, 9.51) were designed by Rivest [1055, 1035]. An Australian extension of MD5 known as HAVAL has also been proposed by Zheng, Pieprzyk, and Seberry [1268]. The first published partial attack on MD4 was by den Boer and Bosselaers [324], who demonstrated collisions could be found when Round 1 (of the three) was omitted from the compression function, and confirmed unpublished work of Merkle showing that collisions could be found (for input pairs differing in only 3 bits) in under a millisecond on a personal computer if Round 3 was omitted. More devastating was the partial attack by Vaudenay [1215] on the full MD4, which provided only near-collisions, but allowed sets of inputs to be found for which, of the corresponding four 32-bit output words, three are constant while the remaining word takes on all possible 32-bit values. This revealed the word access-order in MD4 to be an unfortunate choice. Finally, late in 1995, using techniques related to those which earlier allowed a partial attack on RIPEMD (see below), Dobbertin [354] broke MD4 as a CRHF by finding not only collisions as stated in Remark 9.50 (taking a few seconds on a personal computer), but collisions for meaningful messages (in under one hour, requiring 20 free bytes at the start of the messages).
A first partial attack on MD5 was published by den Boer and Bosselaers [325], who found pseudo-collisions for its compression function f, which maps a 128-bit chaining variable and sixteen 32-bit words down to 128-bits; using 216 operations, they found a 16-word message X and chaining variables S1 =S2 (these differing only in 4 bits, the most significant of each word), such that f(S1,X) = f(S2,X). Because this specialized internal pseudo-collision could not be extended to an external collision due to the fixed initial chaining values (and due to the special relation between the inputs), this attack was considered by many to have little practical significance, although exhibiting a violation of the design goal to build a CRHF from a collision resistant compression function. But in May of 1996, us-
380 |
Ch. 9 Hash Functions and Data Integrity |
ing techniques related to his attack on MD4 above, Dobbertin (rump session, Eurocrypt’96) found MD5 compression function collisions (Remark 9.52) in 10 hours on a personal computer (about 234 compress function computations).
Anticipating the feasibility of 264 operations, Rivest [1055] proposed a method to extend MD4 to 256 bits by running two copies of MD4 in parallel over the input, with different initial chaining values and constants for the second, swapping the values of the variable A with the first after processing each 16-word block and, upon completion, concatenating the 128-bit hash-values from each copy. However, in October of 1995 Dobbertin [352] found collisions for the compression function of extended MD4 in 226 compress function operations, and conjectured that a more sophisticated attack could find a collision for extended MD4 itself in O(240) operations.
MD2, an earlier and slower hash function, was designed in 1988 by Rivest; see Kaliski [1033] for a description. Rogier and Chauvaud [1067] demonstrated that collisions can be efficiently found for the compression function of MD2, and that the MD2 checksum block is necessary to preclude overall MD2 collisions.
RIPEMD [178] was designed in 1992 by den Boer and others under the European RACE Integrity Primitives Evaluation (RIPE) project. A version of MD4 strengthened to counter known attacks, its compression function has two parallel computation lines of three 16step rounds. Nonetheless, early in 1995, Dobbertin [353] demonstrated that if the first or last (parallel) round of the 3-round RIPEMD compress function is omitted, collisions can be found in 231 compress function computations (one day on a 66 MHz personal computer). This result coupled with concern about inherent limitations of 128-bit hash results motivated RIPEMD-160 (Algorithm 9.55) by Dobbertin, Bosselaers, and Preneel [355]; but for corrections, see the directory /pub/COSIC/bosselae/ripemd/ at ftp site ftp.esat.kuleuven.ac.be. Increased security is provided by five rounds (each with two lines) and greater independence between the parallel lines, at a performance penalty of a factor of 2. RIPEMD-128 (with 128-bit result and chaining variable) was simultaneously proposed as a drop-in upgrade for RIPEMD; it scales RIPEMD-160 back to four rounds (each with two lines).
SHA-1 (Algorithm 9.53) is a U.S. government standard [404]. It differs from the original standard SHA [403], which it supersedes, only in the inclusion of the 1-bit rotation in the block expansion from 16 to 80 words. For discussion of how this expansion in SHA is related to linear error correcting codes, see Preneel [1004].
Lai and Massey [729] proposed two hash functions of rate 1/2 with 2m-bit hash values,
Tandem Davies-Meyer and Abreast Davies-Meyer, based on an m-bit block cipher with 2m- bit key (e.g., IDEA), and a third m-bit hash function using a similar block cipher. Merkle’s public-domain hash function Snefru [854] and the FEAL-based N-Hash proposed by Miyaguchi, Ohta, and Iwata [886] are other hash functions which have attracted considerable attention. Snefru, one of the earliest proposals, is based on the idea of Algorithm 9.41, (typically) using as E the first 128 bits of output of a custom-designed symmetric 512-bit block cipher with fixed key k = 0. Differential cryptanalysis has been used by Biham and Shamir [137] to find collisions for Snefru with 2 passes, and is feasible for Snefru with 4 passes; Merkle currently recommends 8 passes (impacting performance). Cryptanalysis of the 128bit hash N-Hash has been carried out by Biham and Shamir [136], with attacks on 3, 6, 9, and 12 rounds being of respective complexity 28, 224, 240, and 256 for the more secure of the two proposed variations.
Despite many proposals, few hash functions based on modular arithmetic have withstood attack, and most that have (including those which are provably secure) tend to be relatively
§9.8 Notes and further references |
381 |
inefficient. MASH-1 (Algorithm 9.56), from Committee Draft ISO/IEC 10118-4 [608], evolved from a long line of related proposals successively broken and repaired, including contributions by Jueneman; Davies and Price; A. Jung; Girault [457] (which includes a summary); and members of ISO SC27/WG2 circa 1994-95 (e.g., in response to the cryptanalysis of the 1994 draft proposal, by Coppersmith and Preneel, in ISO/IEC JTC1/SC27 N1055, Attachment 12, “Comments on MASH-1 and MASH-2 (Feb.21 1995)”). Most prominent among prior proposals was the sqmodn algorithm (due to Jung) in informative Annex D of CCITT Recommendation X.509 (1988 version), which despite suffering ignominy at the hands of Coppersmith [275], was resurrected with modifications as the basis for MASH-1.
§9.5
Simmons [1146] notes that techniques for message authentication without secrecy (today called MACs) were known to Simmons, Stewart, and Stokes already in the early 1970s. In the open literature, the idea of using DES to provide a MAC was presented already in Feb. 1977 by Campbell [230], who wrote “ ... Each group of 64 message bits is passed through the algorithm after being combined with the output of the previous pass. The final DES output is thus a residue which is a cryptographic function of the entire message”, and noted that to detect message replay or deletion each message could be made unique by using per-message keys or cryptographically protected sequence numbers. Page 121 of this same publication describes the use of encryption in conjunction with an appended redundancy check code for manipulation detection (cf. Figure 9.8(b)).
The term MAC itself evolved in the period 1979-1982 during development of ANSI X9.9 [36], where it is defined as “an eight-digit number in hexadecimal format which is the result of passing a financial message through the authentication algorithm using a specific key.” FIPS 81 [398] standardizes MACs based on CBC and CFB modes (CFB-based MACs are little-used, having some disadvantages over CBC-MAC and apparently no advantages); see also FIPS 113 [400]. Algorithm 9.58 is generalized by ISO/IEC 9797 [597] to a CBC-based MAC for an n-bit block cipher providing an m-bit MAC, m ≤ n, including an alternative to the optional strengthening process of Algorithm 9.58: a second key k (possibly dependent on k) is used to encrypt the final output block. As discussed in Chapter 15, using ISO/IEC 9797 with DES to produce a 32-bit MAC and Algorithm 9.29 for padding is equivalent to the MAC specified in ISO 8731-1, ANSI X9.9 and required by ANSI X9.17. Regarding RIPE-MAC (Example 9.63) [178], other than the 2−64 probability of guessing a 64-bit MAC, and MAC forgery as applicable to all iterated MACs (see below), the best known attacks providing key recovery are linear cryptanalysis using 242 known plaintexts for RIPEMAC1, and a 2112 exhaustive search for RIPE-MAC3. Bellare, Kilian, and Rogaway [91] formally examine the security of CBC-based MACs and provide justification, establishing (via exact rather than asymptotic arguments) that pseudorandom functions are preserved under cipher block chaining; they also propose solutions to the problem of Example 9.62 (cf. Remark 9.59).
The MAA (Algorithm 9.68) was developed in response to a request by the Bankers Automated Clearing Services (U.K.), and first appeared as a U.K. National Physical Laboratory Report (NPL Report DITC 17/83 February 1983). It has been part of an ISO banking standard [577] since 1987, and is due to Davies and Clayden [306]; comments on its security (see also below) are offered by Preneel [1003], Davies [304], and Davies and Price [308], who note that its design follows the general principles of the Decimal Shift and Add (DSA) algorithm proposed by Sievi in 1980. As a consequence of the conjecture that MAA may show weaknesses in the case of very long messages, ISO 8731-2 specifies a special mode of operation for messages over 1024 bytes. For more recent results on MAA including ex-
382 |
Ch. 9 Hash Functions and Data Integrity |
ploration of a key recovery attack, see Preneel and van Oorschot [1010].
Methods for constructing a MAC algorithm from an MDC, including the secret prefix, suffix, and envelope methods, are discussed by Tsudik [1196]; Galvin, McCloghrie, and Davin [438] suggest addressing the message extension problem (Example 9.65) in the secret suffix method by using a prepended length field (this requires two passes over the message if the length is not known a priori). Preneel and van Oorschot [1009] compare the security of these methods; propose MD5-MAC (Algorithm 9.69) and similar constructions for
customized MAC functions based on RIPEMD and SHA; and provide Fact 9.57, which applies to MAA (n = 64 = 2m) with u = 232.5 and v = 232.3, while for MD5-MAC
(n = 128 = 2m) both u and v are on the order of 264. Remark 9.60 notwithstanding, the use of an n-bit internal chaining variable with a MAC-value of bitlength m = n/2 is supported by these results.
The envelope method with padding (Example 9.66) is discussed by Kaliski and Robshaw (CryptoBytes vol.1 no.1, Spring 1995). Preneel and van Oorschot [1010] proposed a key recovery attack on this method, which although clearly impractical by requiring over 264 known text-MAC pairs (for MD5 with 128-bit key), reveals an architectural flaw. Bellare, Canetti, and Krawczyk [86] rigorously examined the security of a nested MAC construction (NMAC), and the practical variation HMAC thereof (Example 9.67), proving HMAC to be secure provided the hash function used exhibits certain appropriate characteristics. Prior to this, the related construction h(k1||h(k2||x)) was considered in the note of Kaliski and Robshaw (see above).
Other recent proposals for practical MACs include the bucket hashing construction of Rogaway [1065], and the XOR MAC scheme of Bellare, Gu´erin, and Rogaway [90]. The latter is a provably secure construction for MACs under the assumption of the availability of a finite pseudorandom function, which in practice is instantiated by a block cipher or hash function; advantages include that it is parallelizable and incremental.
MACs intended to provide unconditional security are often called authentication codes (cf. §9.1 above), with an authentication tag (cf. MAC value) accompanying data to provide origin authentication (including data integrity). More formally, an authentication code involves finite sets S of source states (plaintext), A of authentication tags, and K of secret keys, and a set of rules such that each k K defines a mapping eK : S → A. An (authenticated) message, consisting of a source state and a tag, can be verified only by the intended recipient (as for MACs) possessing a pre-shared key. Wegman and Carter [1234] first combined one-time pads with hash functions for message authentication; this approach was pursued by Brassard [191] trading unconditional security for short keys.
This approach was further refined by Krawczyk [714] (see also [717]), whose CRC-based scheme (Algorithm 9.72) is a minor modification of a construction by Rabin [1026]. A second LFSR-based scheme proposed by Krawczyk for producing m-bit hashes (again combined with one-time pads as per Algorithm 9.72) improves on a technique of Wegman and Carter, and involves matrix-vector multiplication by an m×bbinary Toeplitz matrix A(each left-to-right diagonal is fixed: Ai,j = Ak,l for k − i = l − j), itself generated from a random binary irreducible polynomial of degree m (defining the LFSR), and m bits of initial state. Krawczyk proves that the probability of successful MAC forgery here for a b-bit message is at most b/2m−1, e.g., less than 2−30 even for m = 64 and a 1 Gbyte message (cf. Fact 9.73). Earlier, Bierbrauer et al. [127] explored the relations between coding theory, universal hashing, and practical authentication codes with relatively short keys (see also Johansson, Kabatianskii, and Smeets [638]; and the survey of van Tilborg [1211]). These and other MAC constructions suitable for use with stream ciphers are very fast, scalable,
§9.8 Notes and further references |
383 |
and information-theoretically secure when the short keys they require are used as one-time pads; when used with key streams generated by pseudorandom generators, their security is dependent on the stream and (at best) computationally secure.
Desmedt [335] investigated authenticity in stream ciphers, and proposed both unconditionally secure authentication systems and stream ciphers providing authenticity. Lai, Rueppel, and Woollven [731] define an efficient MAC for use with stream ciphers (but see Preneel [1003] regarding a modification to address tampering with ends of messages). Part of an initial secret key is used to seed a key stream generator, each bit of which selectively routes message bits to one of two feedback shift registers (FSRs), the initial states of which are part of the secret key and the final states of which comprise the MAC. The number of pseudorandom bits required equals the number of message bits. Taylor [1189] proposes an alternate MAC technique for use with stream ciphers.
§9.6
Simmons [1144] notes the use of sealed authenticators by the U.S. military. An early presentation of MACs and authentication is given by Meyer and Matyas [859]; the third or later printings are recommended, and include the one-pass PCBC encryption-integrity method of Example 9.91. Example 9.89 was initially proposed by the U.S. National Bureau of Standards, and was subsequently found by Jueneman to have deficiencies; this is included in the extensive discussion by Jueneman, Matyas, and Meyer [645] of using MDCs for integrity, along with the idea of Example 9.90, which Davies and Price [308, p.124] also consider for n = 16. Later work by Jueneman [644] considers both MDCs and MACs; see also Meyer and Schilling [860]. Davies and Price also provide an excellent discussion of transaction authentication, noting additional techniques (cf. §9.6.1) addressing message replay including use of MAC values themselves from immediately preceding messages as chaining values in place of random number chaining. Subtle flaws in various fielded data integrity techniques are discussed by Stubblebine and Gligor [1179].
§9.7
The taxonomy of preimages and collisions is from Preneel [1003]. The alternate terminology of Note 9.94 is from Lai and Massey [729], who published the first systematic treatment of attacks on iterated hash functions, including relationships between fixed-start and freestart attacks, considered ideal security, and re-examined MD-strengthening. The idea of Algorithm 9.92 was published by Yuval [1262], but the implications of the birthday paradox were known to others at the time, e.g., see Merkle [850, p.12-13]. The details of the memoryless version are from van Oorschot and Wiener [1207], who also show the process can be perfectly parallelized (i.e., attaining a factor r speedup with r processors) using parallel collision search methods; related independent work (unpublished) has been reported by Quisquater.
Meet-in-the-middle chaining attacks can be extended to handle additional constraints and otherwise generalized. A “triple birthday” chaining attack, applicable when the compression function is invertible, is given by Coppersmith [267] and generalized by Girault, Cohen, Campana [460]; see also Jueneman [644]. For additional discussion of differential cryptanalysis of hash functions based on block ciphers, see Biham and Shamir [138], Preneel, Govaerts, and Vandewalle [1005], and Rijmen and Preneel [1050].
