Groups-7

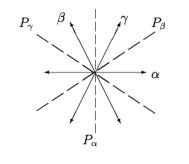
7Система простых корней для алгебры Ли

Из материала предыдущей лекции следует,что структура коммутационных соотношений алгебры Ли может быть закодирована в геометрию набора корневых векторов.Обозначим набор корневых векторов для алгебры Ли g: (g). В частности , понятно , что отражения (73)сохраняют этот набор.

Определение35 Группа,которая порождается всеми отражениями(73),называется группой Вейля.

7.1Положительные корни и матрица Картана

Рассмотрим в корневом пространстве гиперплоскость P перпендикулярную корню . Очевидно,что весь набор корневых векторов разбивается на два поднабора,расположенных по двум сторонам любой гиперплоскости P .

Разделить эти наборы можно следующим образом. r-мерное векторное пространство делится всеми гиперплоскостями на неперекрывающие конусы,каждый из которого называется камерой Вейля.В случае алгебры g = sl(3) имеется три гиперплоскости,которые делят двумерное пространство на6камер Вейля:Выберем некоторую камеру Вейля и

Рис. 3: Камеры Вейля для алгебры sl(3)

возьмем вектор x,лежащий внутри этой камеры.При этом должно выполняться условие (x, ) 6= 0, 8 2 (g) иначе вектор x лежал бы в одной из гиперплоскостей.Очевидно, что (x, ) не меняет знак( 8 2 (g)) при движении x внутри одной и той же камеры, в противном случае была бы пройдена точка (x, ) = 0 и вектор x оказался бы в другой камере.

79

Определение36 Зафиксируем камеру Вейля и вектор x в ней . Все множество корней делится по отношению к выбранной камере на два множества:

Камера Вейля в которой располагается вектор x называется доминантной.

Лемма2 Если векторы i, i = 1, . . . , k r положительны и ( i, j ) 0, 8i, j (i 6= j), то набор векторов i линейно независим.

Док-во. Будем доказывать эту лемму от противного.Пусть справедливо обратное утверждение

фициентов должна быть отрицательной.Перенумерацией корней всегда можно добиться чтобы отрицательные коэффициенты соответствовали корням i, i = 1, . . . , l, где l < k.

Перенесем их в правую часть равенства(82)с изменением знака и переобозначением ui ! −vi. Тогда вместо равенства (82) получим

где теперь вещественные коэффициенты vi и ui неотрицательны.Вычислим квадрат вектора "

откуда следует,что " = 0 является нулевым вектором.Но тогда справедливы равенства

откуда из положительности корней i : ( i, x) > 0 и неотрицательности коэффициентов vi, i = 1, . . . , l и ui, i = l + 1, . . . , k следует,что все коэффициенты в(82)равны нулю.

80

Определение37 Положительный корень называется простым,если его нельзя представить в виде суммы двух положительных корней.

Теорема13 Существует ровно r (где число r называется рангом алгебры Ли)простых корней ( 1, 2, . . . , r) = + таких,что любой положительный корень можно

записать как

Xr

i=1

где ni ≥ 0 – неотрицательные целые числа , а любой отрицательный кореньβ представим

в виде

Xr

где целые числа mi 0. Более того скалярные произведения любой пары простых кор - ней ( i, j ) 0 всегда отрицательно,что означает,что угол между двумя простыми корнями всегда больше или равен 90◦.

вся струна корней лежит с одной стороны некоторой гиперплоскости и если корень γ положительный,значит и вся струна состоит из положительных корней по отношению к

некоторой гиперплоскости.Например,если j = 2(γ, ) – четное , то такая гиперплоскость

2

определяется корнем γ − j /2.

Пусть положительный корень γ и простой положительный корень таковы,что последний корень в этой струне γ − j , где j – целое неотрицательное число , является про - стым корнем.Обозначим простой корень γ − j как β.Тогда исходный положительный корень γ равен β + j и для целого неотрицательного числа j справедливо равенство

Таким образом,согласно Лемме2все простые корни являются линейно независимыми.

81

По определению положительные корни являются либо простыми либо разлагаются на сумму положительных корней.Так как метрика Киллинга(60)позволяет выразить компоненту yi любого вектора в корневом пространстве по формуле

X

2 +

то в конечном итоге любой вектор может быть представлен как линейная комбинация простых корней.Это означает,что в качестве базиса корневого пространства можно взять набор простых корней,откуда следует,что их должно быть ровно r-штук: = ( 1, . . . , r).

Далее система векторов { 1, . . . , r, β}, где β –положительный не простой корень,является линейно зависимой и согласно леммы2по крайне мере одно из скалярных произведений ( j , β) > 0. Тогда по лемме 1 вектор γ1 = β− j тоже корень,причем положительный (иначе j будет не простым).Теперь либо γ1 – простой корень и соответственно ,β разлагается в виде суммы двух простых корней,либо γ1 опять положительный не простой корень такой,что система векторов { 1, . . . , r, γ1} опять линейно зависима,а значит вектор γ1 может быть снова разложен в виде γ2 = γ1 − k, где (γ1, k) > 0 для некоторого k, тогда опять из-за леммы2 γ2 является положительным корнем,а индекс k либо равен индексу j либо отличается от него.Корень γ2 опять либо простой либо положительный.Продолжая эту процедуру получим на m-ом шаге простой корень γm. Итак в результате этой проце - дуре любой положительный корень может быть представлен в виде линейной комбинации простых корней с положительными целыми коэффициентами.Соответственно,любой отрицательной корень может быть разложен в виде линейной комбинации простых корней с неположительными целыми коэффициентами.

Очевидно,что разность двух простых корней 1 и 2 не может быть корнем.Действительно, β = 1 − 2 не может быть положительным корнем(иначе 1 разлагался бы на сумму двух положительных корней и не был бы простым).Аналогично β не может быть отрицательным корнем(иначе 2 = 1 + (−β) разлагался бы в сумму двух положительных корней и не был бы простым).Таким образом β не корень.Из этого наблюдения немедленно следует соотношение

82

где h обозначает r-мерный вектор компонентами которого являются генераторы подалгебры Картана h = (h1, . . . , hr).

Из теоремы13вытекает также следующее следствие.Разность двух корней γ = β − ik , где корень β есть сумма простых корней β = i1 + i2 + . . .+ ij и ik 6= i1, . . . , ij не является корнем.Действительно, γ не может быть отрицательным корнем(иначе ik не является простым корнем).С другой стороны, γ не может быть положительным корнем так как это противоречило бы(83).

Теорема14 Любая простая алгебра Ли g определяется системой своих простых корней.

Док-во. Для доказательства этой теоремы достаточно построить по простым корням алгебры g все ее корни.Если – корень , то− –тоже корень.Поэтому достаточно построить все положительные корни.Положительный корень,являющийся суммой k простых корней,называется корнем порядка k.Полная система корней строится индуктивной процедурой.Все корни порядка1уже имеются,так как это простые корни.

Пусть по системе простых корней построены все корни порядка k −1.Найдем среди простых корней такие корни j , что (γ, j ) < 0. Тогда корни порядка k имеют вид γ + j .

Сформулируем необходимое условие нахождения простого корня j для заданного положительного корня γ уровня k − 1.Мы знаем,что все корни объединяются в струны

такие,что вектор γ −(m+ 1) j не является корнем.Возможность построения корня γ + j может быть реализована,только если набор корней(87)является частью полной струны вида

такой,что вектор γ + (n + 1) j не является корнем.Длина этой цепочки корней равна n + m + 1 и согласно условиям существования струны корней (72) должно совпадать с

числом

2(γ + n j , j ) + 1 = n + m + 1 ( j , j )

83

Из этого равенства необходимым условием существования вектора γ + j является равенство

или неравенство

2 (γ, j ) < m ( j , j )

Пользуясь этим неравенством можно построить все корни порядка k. Рассмотрим струну корней

где положительное целое число m равно −2( i, j )/( j , j ).Для конечномерных простых алгебр Ли число m может принимать только значения0,1,2,3и,следовательно,число корневых векторов в струне не превышает4.

Итак,возможность построения всех корней алгебры Ли из простых корней означает, что простая конечномерная алгебра Ли g определяется набором образующих

( i, h) e± i , h i = 2( i, i)

которые соответствуют простым корням и удовлетворяют соотношениям

называется матрицей Картана,а конечномерность алгебры Ли обеспечивается соотношениями

1−kij

называются соотношениями Серра.Образующие простой алгебры Ли g: {e± i , h i } в ко - личестве 3r штук называются образующими или генераторами Шевалье.

84

Очевидно,что kii = 2 и kij 0 для всех i 6= j.Для недиоганальных элементов матрицы Картана имется согласно(76)следующие возможности:

В случае простых алгебр Ли ранга два,то есть в случае двумерности пространств в которых располагается корневые системы,согласно(93)можно построить три корневые системы показанные на рисунке4.

Рис. 4: Корневые системы всех простых алгебр Ли ранга2 ( (i) i).

Из этого рисунка видна структура струн корней типа(89)для простых алгебр Ли ранга 2.Например,струны имеющие на концах простые корни для первой структуры корней имеют вид

1, 1 + 2 и 2, 2 + 1

и соответствуют двум двумерным присоединенным представлениям относительно sl2-подалгебр, ассоциированных с простыми корнями 2 и 1 соответственно.

Для второй структуры корней,показанной на рисунке4,струны имеют вид

1, 1 + 2 и 2, 2 + 1, 2 + 2 1

соответствующие двумерному и трехмерному представлению относительно sl2-подалгебр.

85

Относительно подалгебры связанной с корнем 2, составной корень 2 + 2 1 образует одномерное представление.

Наконец для третьей структуры корней,показанной на рисунке4,струны имеют вид

1, 1 + 2 и 2, 2 + 1, 2 + 2 1, 2 + 3 1

Относительно sl2-подалгебры,ассоциированной с простым корнем 1, составной корень 2 2 + 3 1 соответствует одномерному представлению,а относительно sl2-подалгебры,ас- социированной с простым корнем 2, корень 2 + 2 1 и два корня 2 2 + 3 1, 2 + 3 1 образуют одномерное и двумерное представления этой подалгебры.

7.2Диаграмы Дынкина и корневые системы

Из сказанного выше следует,что вся информация о структуре алгебры Ли закодирована в недиагональных элементах матриц Картана.Матрицу Картана можно представить графически с помощью диаграмм Дынкина.Это можно сделать с помощью следующих правил.

1.Необходимо нарисовать r = rang(g) точек,соответствующих простым корням i

(i = 1, . . . , r).

2.Соединить i-ую и j-ую точку с помощью kij kji линий(число таких линий может быть только0,1,2или3).

3.Если между точками i и j проходит больше одной линии необходимо нарисовать стрелку указывающую корень с меньшей длиной.

Диаграммы Дынкина,которые соответствуют векторным диаграммам,представленным на рисунке4имеют вид,показанный на рисунке5.

Из анализа геометрии возможных корневых конфигураций можно получить информацию о всех возможных алгебрах Ли,то есть решить задачу классификации этих математических структур.Из этого анализа следует,что существует четыре серии алгебр размер которых определяется положительным целым числом `.

Первая серия,обозначаемая символом Al,имеет диаграмму Дынкина,показанную на рисунке6.Все корни в этой диаграмме имеют одинаковую длину.Алгебры из этой серии

86

Рис. 5: Диаграммы Дынкина для всех простых алгебр Ли ранга2 ( (i) i).

Рис. 6: Диаграммы Дынкина для серии простых алгебр Ли Al.

соответствуют алгебрам sll+1.

Вторая и третья серии,обозначаемые символами Bl и Cl,имеют диаграммы Дынкина,показанные на рисунке7.Корни в этих диаграммах имеют разные длины,при этом

Рис. 7: Диаграммы Дынкина для серии простых алгебр Ли Bl и и Cl.

для серии алгебр Bl все корни за исключением одного одинаковые и их квадраты длин вдвое больше,чем квадрат l-того корня.Для серии алгебр Cl ситуация обратная: l-тый корень имеет квадрат длины в два раза больший чем остальные корни.Алгебры серии Bl соответствуют простым алгебрам Ли so2l+1. Алгебры серии Cl соответствуют простым алгебрам Ли sp2l.

Четвертая серия,обозначаемая символом Dl,имеет диаграмму Дынкина,показанную на рисунке8.Все корни в этой диаграмме также имеют одинаковую длину.Алгебры из

87

Рис. 8: Диаграммы Дынкина для серии простых алгебр Ли Dl.

этой серии соответствуют алгебрам so2l.

Кроме бесконечно-мерных серий существует пять конечно-мерных(исключительных) алгебр Ли.Первые три алгебры этого типа обозначаются символами E6, E7 и E8.Диаграммы Дынкина для этих алгебр Ли показаны на рисунке9.Все корни этих исключительных

Рис. 9: Диаграммы Дынкина для исключительных простых алгебр Ли E6, E7 и E8.

алгебр имеют одинаковую длину.

Последние две конечномерные исключительные алгебры обозначаются символами F4 и G2.Диаграммы Дынкина для этих алгебр Ли показаны на рисунке10.Простые корни

88