
Пример 3
Разберем еще один пример:
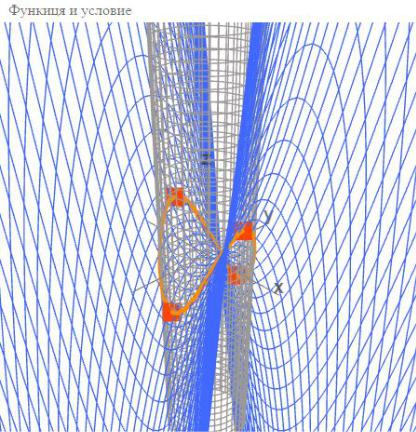
f (x, y)= x2 − y2 и ограничение ϕ(x, y): x2 + y2 =1. Функция f (x, y) - седло, а ϕ(x, y) - цилиндр с центром в начале координат, радиуса 1 и параллельного оси аппликат.
Составим функцию Лагранжа:
L(x, y,λ)= x2 − y2 +λ (x2 + y2 −1)
Приравняем к нулю ее частные производные:
|
|
|
|
∂ |
|
|
L = |
2x + 2λx = 0 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
∂x |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
∂ |
L = −2y + 2λy = 0 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
∂y |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
∂ |
|
|
= x |
2 |
+ y |
2 |
−1 = 0 |
|
|
|
|
|||
|
|
∂λ |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Упростим выражения: |
|
|
|
|
||||||||||||||
|
|
|
2x + 2λx = 0 |
|
2x (1 |
+λ)= 0 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−2y + 2λy = 0 |
2y (−1+λ)= 0 |
|||||||||||||||||
|
|
|
|
2 |
|
+ y |
2 |
−1 = 0 |
|
2 |
+ y |
2 |
−1 = 0 |
|||||
x |
|
|
|
x |
|
|
||||||||||||
Тогда получается, что есть вариант x = 0, y = 0 , однако эта точка не удовлетворяет условию связи. Значит далее будем учитывать, что x и y не могут одновременно обращаться в ноль (x2 + y2 ≠ 0 ). Можно разделить решение на 2 случая:
2x (1+λ)= 0 |
λ = −1 |
||||
|
|
|
|
|
|
2y (−1+λ)= 0 |
y = 0 |
||||
|
2 |
+ y |
2 |
−1 = 0 |
|
x |
|
|
x = ±1 |
||
И наоборот: |
|
||||
2x (1 |
+λ)= 0 |
x = 0 |
|||
|
|
|
|
|
|
2y (−1+λ)= 0 |
λ =1 |
||||
|
2 |
+ y |
2 |
−1 = 0 |
|
x |
|
|
y = ±1 |
||
Снова получили две функции Лагранжа (т.к. нашли два различных λ ):
L1 (x, y,λ)= x2 − y2 +1 (x2 + y2 −1) L2 (x, y,λ)= x2 − y2 −1 (x2 + y2 −1)
Преобразуем эти функции:
L1 (x, y)= x2 − y2 + x2 + y2 −1 = 2x2 −1 L2 (x, y)= x2 − y2 − x2 − y2 +1 = −2y2 +1
11
Обе функции – параболические цилиндры.
Для L1 можно приравнять производную к нулю и получить, что x = 0, но как теперь найти y ? Ответ:
подставить в уравнение связи: ϕ(0, y): 02 + y2 =1 y = ±1. Причем точки M 0 |
= [x = |
0 |
, y =1] |
||
и M1 = [x = 0 , y = −1] будут точками локального |
минимума (следует |
из |
положительной |
||
определенности второго дифференциала функции L1 ). |
|
|
|
|
|
Аналогично для функции L2 получаем точки M 2 = [x = −1 |
, y = 0] и M 3 = [x =1 |
, |
|
y = 0]. Это |
|
будут точки локального максимума (из отрицательной определенности второго дифференциала функции L2 ).
Тогда имеем следующие графики:
Рисунок 7 - Функция fи условие(цилиндр). Имеется 4 точки экстремума (оранжевые точки)
12
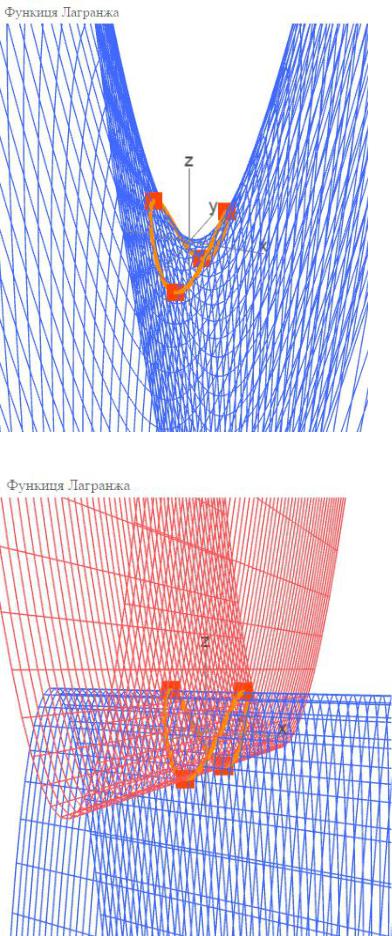
Рисунок 8 - Ещене сдвинутыефункции Лагранжа
Рисунок 9 - Функции Лагранжа. L1 – красная,L2 – синяя
13
