
#тои zanyatie_9
.pdfТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНФОРМАТИКИ
Практическое занятие №9
к.т.н, доцент Ямпольский Сергей Михайлович
Тема №7
Помехоустойчивое кодирование
●Линейные помехоустойчивые коды
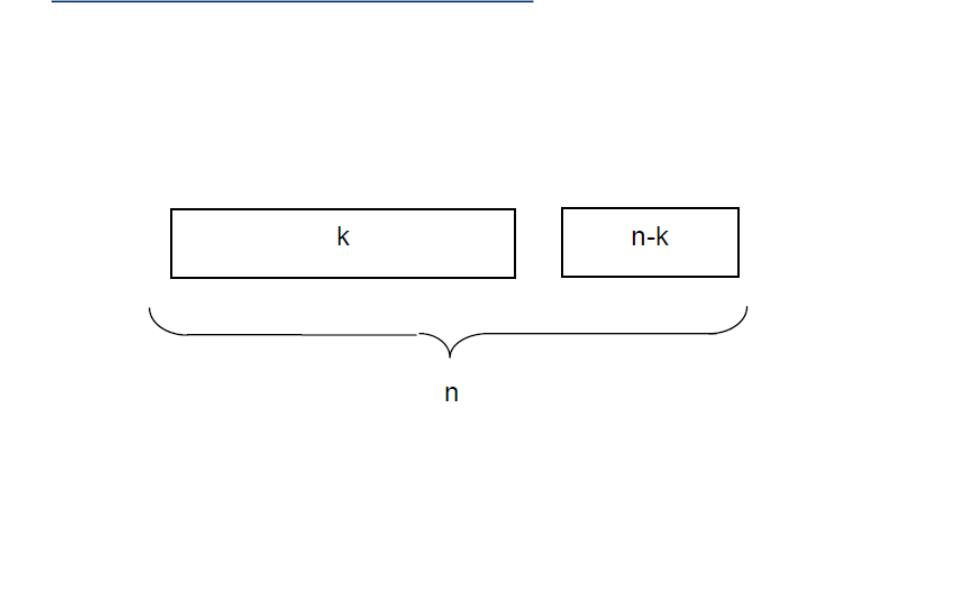
●Линейные помехоустойчивые коды - это (n,k)-разделимые коды, в которых кодовые комбинации состоят из информационной и проверочной части
Информационные Проверочные cимволы - k cимволы - r
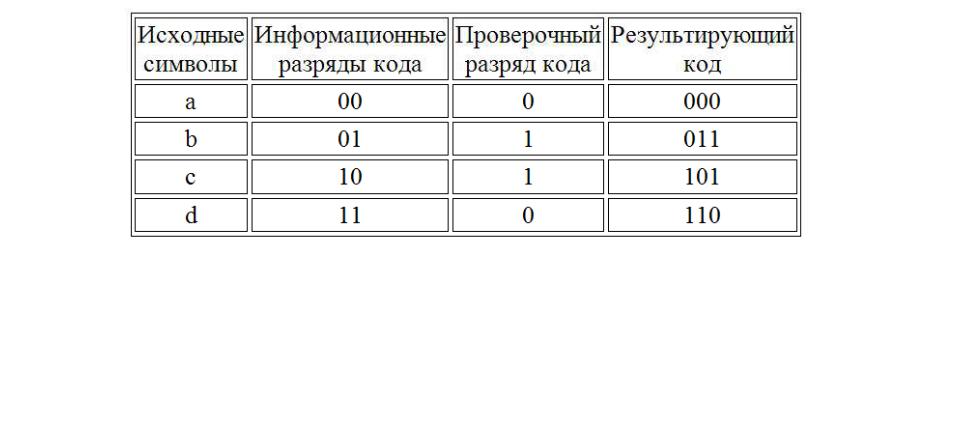
● Проверочные символы кодов образуются с помощью линейных операций над информационными символами
● Линейные помехоустойчивые коды
Проверочные символы кодов образуются с помощью линейных операций над информационными символами

● Коды Хемминга
Коды Хемминга (линейные помехоустойчивые (n,k)-коды) позволяют исправлять одиночную ошибку, с помощью непосредственного описания
Для r =3, 4, 5… существует классический код Хемминга с маркировкой (7,4), (15,11), (31,26) …
2к ≤ |
2n |
|
|
2n |
n = 2r −1 |
||||
1 |
1 |
≤ |
|||||||
|
i |
1+Cn |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑Cn |
|
|
2 |
|
k = 2 |
r |
−1 |
−r |
|
i=0 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
● Коды Хемминга
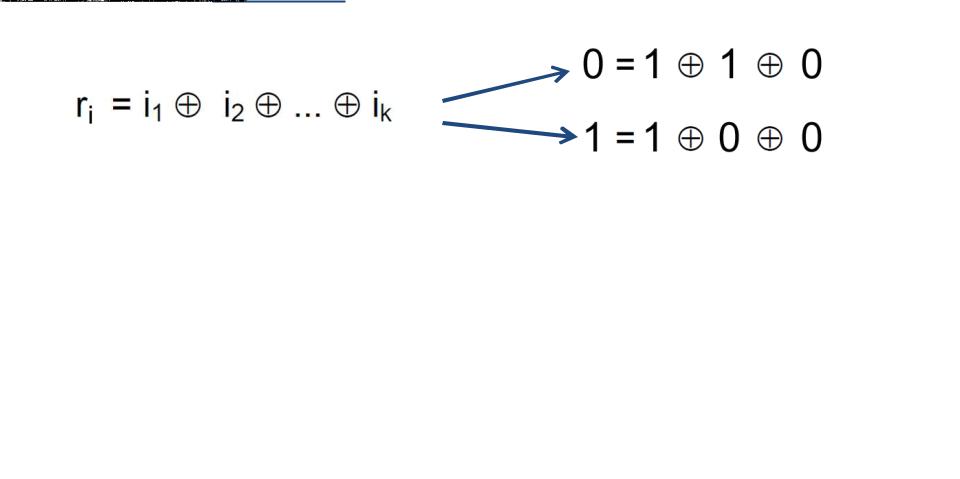
Построение кодов Хемминга основано на принципе проверки на четность числа единичных символов:
к последовательности символов добавляется элемент, чтобы число единичных символов в получившейся последовательности было четным

●Классический (7,4) код Хемминга
Вдекодере в режиме исправления ошибок строится последовательность синдромов:
Признаком отсутствия ошибки в принятой кодовой последовательности является четность числа единиц
● Коды Хемминга
Способы описания кодов Хемминга
Табличный |
Проверочная |
способ |
матрица |
|
Порождающая |
|
матрица |

● Табличный способ
Таблица 16 кодовых слов (7,4)-кода Хемминга
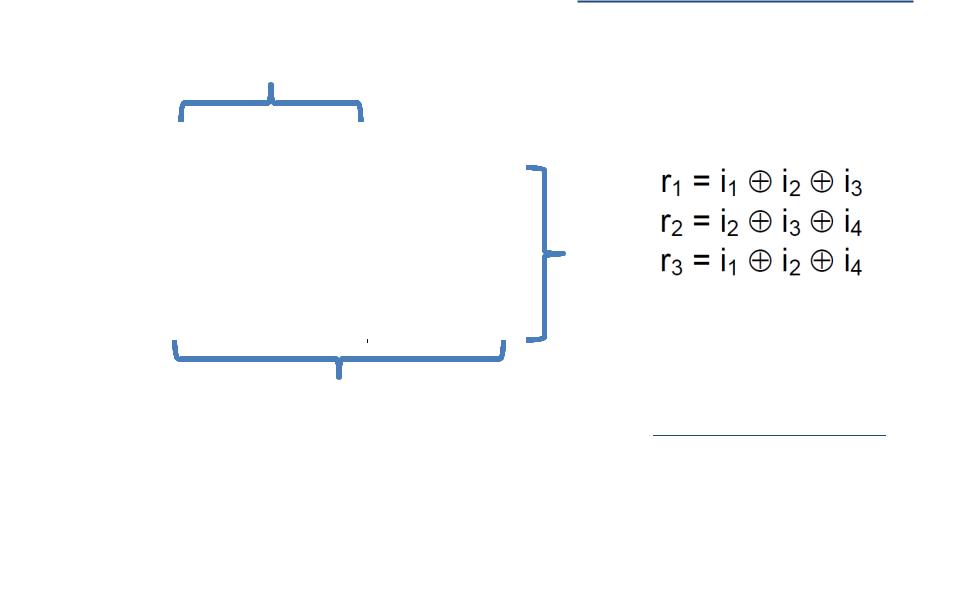
● Порождающая матрица
Код Хемминга полностью определяется порождающей матрицей
(размером k*n) строки которой являются кодовыми словами
k
|
i1 |
i2 |
i3 |
i4 |
|
|
r1 |
r2 |
r3 |
|
|
|
|
|
|||||||
|
|
|
|
|||||||
|
|
|
|
|||||||
G = |
1 |
0 |
0 |
0 |
|
|
1 |
0 |
1 |
k |
|
||||||||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
0 |
1 |
0 |
0 |
|
1 |
1 |
||||
|
|
1 |
||||||||
|
||||||||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
0 |
0 |
1 |
0 |
|
1 |
0 |
|
||
|
|
|
1 |
|
||||||
|
|
|
||||||||
|
|
|
|
|||||||
|
|
|
|
|||||||
|
0 |
0 |
0 |
1 |
|
|
|
1 |
1 |
|
|
|
|
||||||||
|
|
|
0 |
|
||||||
|
|
|
||||||||
|
|
|
|
|||||||
|
|
|
|
|||||||
|
|
|
|
|
n |
|
|
|
||
●Информационные символы матрицы - это элементы единичной матрицы (размером k*k), а проверочные символы матрицы определяются через информационные
●Строки порождающей матрицы являются кодовыми словами, а все остальные кодовые слова являются линейными комбинациями строк порождающей матрицы
