2. Совершенные нигде не плотные множества на плоскости7

2.1 Кладбище Серпинского

Построим на плоскости интересное множество Вследующим образом: разделим, квадратпрямымина 9 равных квадратов и выбросим их них пять открытых, не примыкающих к вершинам исходного квадрата. Затем, каждый из оставшихся квадратов также разделим на 9 частей, и выбросим пять из них, и т.д. Множество, оставшееся после счётного числа шагов, обозначимBи назовёмкладбище Серпинского. Вычислим площадь выброшенных квадратов:

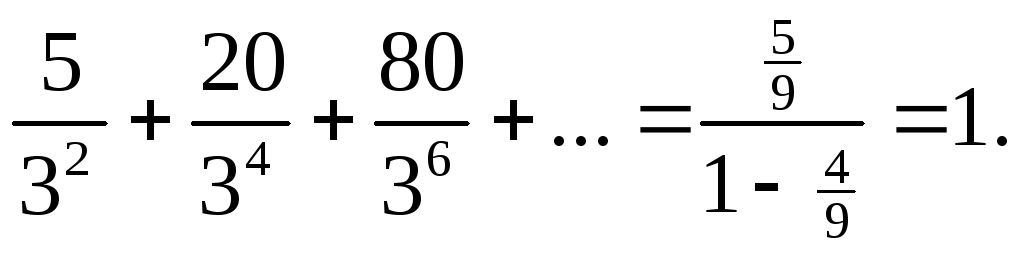
Кладбище Серпинского является совершенным и нигде не плотным множеством.

Заметим фрактальную структуру множества.

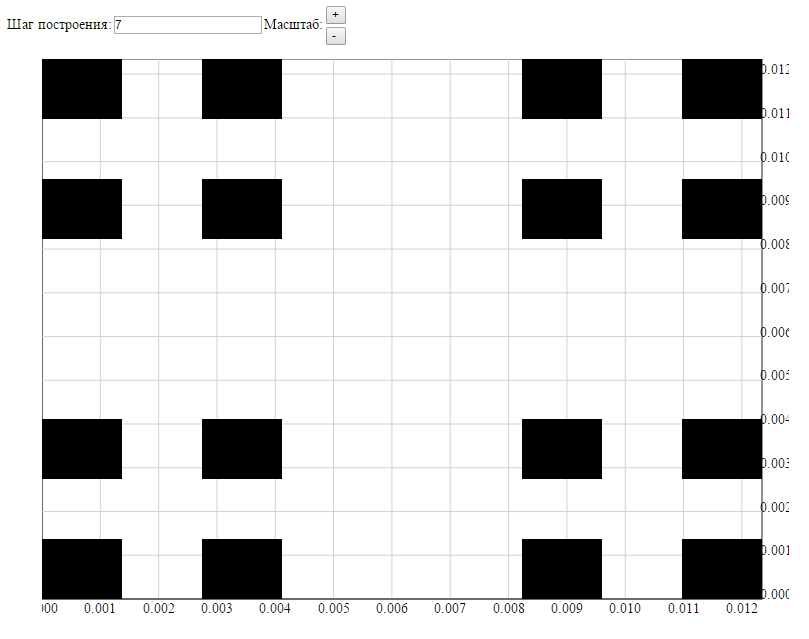
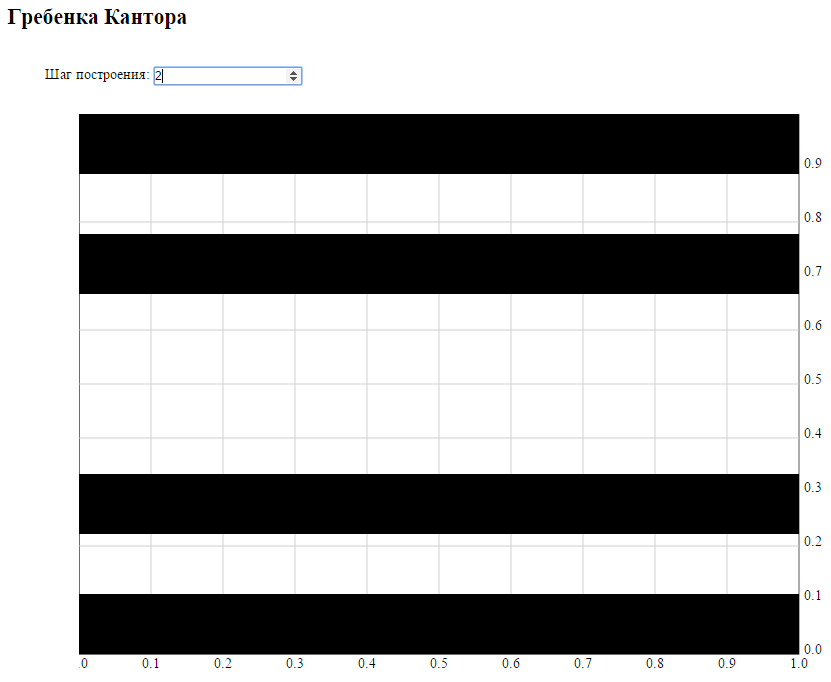
2.2 Гребенка Кантора

Назовём Канторовой гребёнкоймножествоDна плоскостиOxy, состоящее из всех точек,координаты которых удовлетворяют следующим условиям:, где- множество Кантора на осиOy. Канторова гребёнка является совершенным нигде не плотным множеством на плоскости. МножествоD состоит из всех точекисходного единичного квадрата, абсциссы которых произвольны, а ординаты могут быть записаны в виде троичной дроби, не содержащей единицы среди своих троичных знаков.

Можно ли множества B(кладбище Серпинского) иD(гребёнка Кантора) выразить через множество Канторас помощью действий дополнения до отрезка [0, 1] и декартова произведения? Очевидно, что множестваBиDвыражаются элементарно:

B=x

D= [0, 1] x

3 Функция Кантора

Можно ли отобразить непрерывно некоторое нигде не плотное на сегменте [0,1] множество на сам этот отрезок?

Да, возьмём нигде не плотноeмножество Кантора. На первом шаге построения положим в точках смежного интервала первого рода значение функции равное 0,5. На втором шаге каждому смежному интервалу второго рода положим значение функции соответственно 0.25 и 0.75. Т.е. мы как бы делим каждый отрезок на осиOyпополам (y_i) и ставим в соответствующем смежном интервале значение функции равное значению yi.

В результате мы получили неубывающую функцию (было доказано в рамках курса «Избранные главы математического анализа»), определённую на отрезке [0, 1] и постоянную в некоторой окрестности каждой точки из множества [0, 1]\. Построенная функцияназываетсяфункцией Кантора(канторова функция), а её график, приведённый ниже -''чёртовой лестницей''.

Обратите внимание на фрактальную структуру функции:

Функция удовлетворяет следующему неравенству:

Функция Кантора является непрерывной на отрезке [0, 1]. Она не убывает на [0, 1] и множество её значений составляет весь отрезок [0, 1]. Поэтому, функция не имеет скачков. А т.к. монотонная функция не может иметь других точек разрыва, кроме скачков (см. критерий непрерывности монотонных функций), то она является непрерывной.

Любопытным является наблюдение, что график непрерывной функции кантора невозможно нарисовать ''не отрывая карандаша от бумаги''.

4. Всюду непрерывная, но нигде не дифференцируемая функция

Построим вспомогательную функцию на отрезке [0, 1] по шагам. На нулевом шаге зададим две точки:

и .

Далее зафиксируем параметр . На первом и последующем шагах будем задавать точки по следующему правилу: для каждых двух соседних по оси абсцисс ранее построенных точекимы будем строить две новые точкиицентрально-симметрично относительно центра прямоугольника, задаваемого точкамиис коэффициентомk. То есть, на первом шаге задаются две новые точки:

и , и т.д.

На (m+1)-ом шаге в дополнении к ранее построенным точкам с абсциссами

,

строятся по две точки во всех промежутках по оси абсцисс между соседними уже построенными точками. Это построение выполняется так: промежутки по оси абсцисс между соседними точками (прямоугольники со сторонами aиb) делятся на 3 равные части каждый. Затем две новые точки строятся по одной из нижеприведённых схем:

В зависимости от того, какая из соседних точек иливыше, используем левую или правую схему. На первом шаге, как это было показано выше, принимаемa = b = 1.

Повторяем построение счётное число раз при m = 1, 2, 3, … . В результате нами будет получен фрактал, который будет подобен, с точностью до некоторого аффинного преобразования (растяжение, сжатие, поворот) любой своей части, заключенной в каждой полосе:

;

В результате построения фрактала получим функцию , определённую на множестве точек

, ;(*)

которое всюду плотно на отрезке [0, 1].

Какими свойствами обладает построенная функция?

• в каждой точке вида (*) либо строгий максимум, либо строгий минимум, т.е. функция g(x)нигде не монотонная, и имеет плотные на сегменте [0, 1] множества точек строгих экстремумов;

• функция g(x) непрерывна, и даже равномерно непрерывна на множестве точек (*);

• построенная непрерывная на сегменте [0, 1] функция не имеет ни в одной точке данного отрезка даже односторонних производных;

Вышеуказанные свойства были доказаны в рамках курса «Избранные главы математического анализа».

В рассмотренном примере мы полагали параметр . Изменяя значение данного параметра, можно получить семейства функций со своими особыми свойствами.

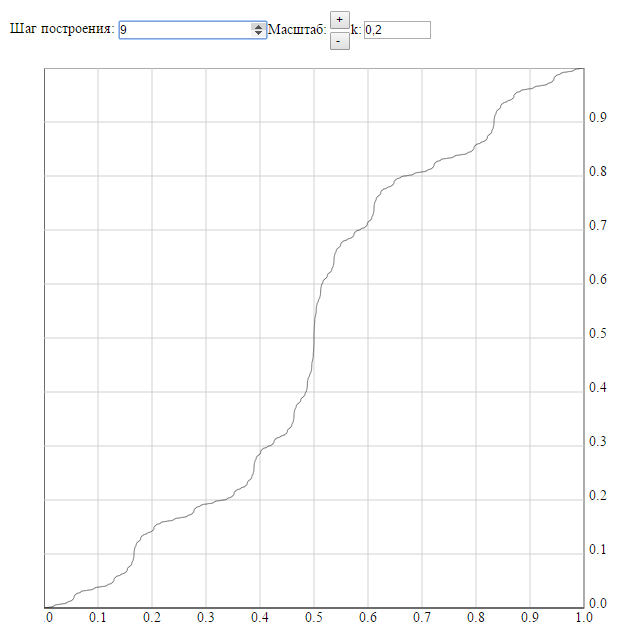
• . Эти функции непрерывны и строго монотонно возрастающие. Имеют нулевые и бесконечные производные (соответственно, точки перегиба) на множествах точек, всюду плотных на сегменте [0, 1].

• . Получена линейная функция y = x

• . Свойства семейства функций те же, что и при значениях к из первого диапазона .

• . Нами получена функция Кантора, которая была подробно изучена нами ранее.

• . Данные функции непрерывны, нигде не монотонны, имеют строгие минимумы и максимумы, нулевые и бесконечные (обоих знаков) односторонние производные на множествах точек, всюду плотных на сегменте [0, 1].

• . Данная функция была изучена нами выше.

• . Функции из этого диапазона обладают теми же свойствами, что и функция при .