
UMK_po_mikroekonomike / 50_лекций по микроэкономике / 50_IV. Пространство благ
.pdf
576 Математическое приложение
Упражнение |
7 |
|
|
|
Рассмотрим |
функцию |
|
|
|
|
ìax, |
x < 0; |
||
|
ï |
1 |
|
|
|
ï |
x, |
0 £ x < 1; |
|
|
f(x) = í |
|
||
|
2 |
|||
|
ïï |
1 |
+ b × (x - 1), x ³ 1. |
|
|
2 |
|||
|
î |
|
|
|
При каких значения а и b эта функция
—выпукла вниз?
—выпукла вверх?
—не имеет постоянного знака выпуклости?
IV. Пространство благ
Основные понятия
Многие теоретические вопросы обсуждаются в нашем учебни ке применительно к случаю двух продуктов. В качестве удобного средства, существенно упрощающего их анализ, использовались г рафические построения, в которых набор, включающий два продукта в коли- чествах x1, è x2 изображался точкой на плоскости с декартовыми координатами (x1, x2). Перевод теоретических понятий на геометри- ческий язык делал свойства обсуждаемых явлений весьма на глядными и при этом не приводил к потере строгости: все геометрические понятия (прямые, кривые, углы наклона и т. п.) имели точно определенные аналитические эквиваленты — уравнения, производные, с оотношения между параметрами и т. д. Поэтому такие построения широко используются и в учебниках по экономике, и в научных публикациях.
Однако эти геометрические рассуждения были строгими и то ч- ными лишь для случаев, когда перечень потребляемых благ в клю- чал всего два наименования. В действительности же число б лаг, которыми пользуются люди, значительно больше. Выводы, пол у- ченные геометрическим путем, можно считать обладающими д остаточной общностью, если их удастся распространить на слу чаи произвольного числа благ.
Будем считать, что мы присвоили всем мыслимым благам номера i = 1,2,..., n, и xi обозначает количество i-того блага. Тогда набор благ Х может быть представлен n числами, расположенными
в порядке номеров благ: |
|
X = (x1,x2,...,xn ). |
(1) |

IV. Пространство благ 577
Под n-мерным пространством благ будем понимать множество числовых наборов вида (1). Каждый такой набор чисел будем называть точкой (элементом) пространства, или вектором, а числа xi — ее координатами, или компонентами.
Рассматривая некоторое пространство благ, мы будем счита ть число компонент n — размерность пространства — фиксированным; более того, на каждом месте в наборе (1) должно стоять количе ство блага определенного вида. Если данный потребитель не испо льзует какое-нибудь, скажем, k-тоe благо, то будем считать xk = 0.
Условимся обозначать точки пространства благ большими латинскими буквами, а их координаты — соответствующими маленькими буквами с индексами — номерами координат. Нам не придется каждый раз пояснять, что, например, z2 — это вторая координата точки Z.
Точки X и Y будем считать равными и записывать Х = Y в том и только том случае, если совпадают все их координаты: xi = yi. Если же точки «одинаковы» в каком-то отношении (скажем, рав - ноценны по потребительским предпочтениям), но имеют неод инаковые координаты, мы будем их считать неравными друг другу.
Реальные наборы благ, разумеется, не могут иметь отрицате льных координат. Тем не менее мы будем рассматривать простр анства, точки которых могут иметь координаты любых знаков, ч тобы в этих пространствах нашлось место не только для реальных наборов, но и для приращений, отклонений, «шагов» и т. д., а также для некоторых условных наборов, которые могут появиться в различных мысленных экспериментах.
Арифметические операции
Рассмотрим задачу, чрезвычайно похожую на те, с которых на чинается изучение математики. Некий гражданин приобрел набор продуктов X, а его жена — набор Y. Спрашивается, сколько они купили вместе?
То, что они приобрели вместе — набор продуктов Z — естественно считать суммой Z = X + Y. При этом каждая компонента zi есть сумма соответствующих компонент xi è yi:
zi = xi + yi, i = l,2,...,n. |
(2) |
Равенство (2), соответствующее содержательному смыслу «сл ожения» наборов, мы будем рассматривать в качестве определен ия суммы точек пространства благ. Легко проверить, что определе нная таким образом операция сложения обладает обычными свойствами
X + Y = Y + X; (X + Y) + Z = X + (Y + Z),
что позволяет рассматривать суммы вида Х + Y +... + W, не
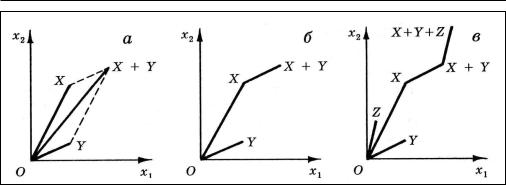
578 Математическое приложение
Рис. 1. Сложение элементов двумерного пространства: правил о параллелограмма (а); правило параллельного переноса для двух слагаемых (б); правило параллельного переноса для произвольного числа слагаем ых в().
заботясь ни о порядке слагаемых, ни о последовательности выполнения операций сложения.
В пространствах двух и трех измерений сложение можно опре - делить чисто геометрически — с помощью «правила параллелограмма» (рис. 1,а) или «параллельного переноса» (рис. 1,б). Такое геометрическое определение равносильно определению (2). Правило «параллельного переноса» удобнее в том отношении, что мож ет быть распространено на произвольное число слагаемых (рис . 1,в).
Операцию вычитания можно определить как обратную по отно - шению к сложению. Будем называть точку Z разностью точек Х и Y и обозначать Z = Х – Y, если Z + Y = X. При этом
|
zi |
= xi – yi, |
i= 1,2. ...,n. |
(3) |
Особую |
ðîëü |
в нашем пространстве играет нулевой элемент O = |
||
= (0,0,...,0) — |
«начало координат». Для любого Х справедливы |
|||
равенства |
Õ + O = Õ, Õ – Õ = O. |
|
||
Для каждого |
элемента |
Х существует противоположный элемент, |
||
который мы будем обозначать –X; мы можем определить его следу- |
|
ющим образом: – Х = O – Х. Чтобы перейти от точки Х к точке – |
|
X, нужно |
знаки всех ее компонент изменить на противоположн ые. |
Точка –X |
симметрична точке Х относительно начала координат О. |
Следующая арифметическая операция — умножение элемента
пространства на число. Для любого вещественного числа а |
опреде- |
||
лим произведение αX = Y |
как такую |
точку, для которой |
|
yi = αxi, |
i = 1,2,...,n. |
|
(4) |
В пространствах двух и трех измерений произведению векто ра на число можно дать простое геометрическое определение (рис. 2).

IV. Пространство благ 579
Рис. 2. Умножение элемен- |
Рис. 3. Сдвиг на плоско- |
Рис. 4. Гомотетия на |
та двумерного простран- |
ñòè. |
плоскости. |
ства на число (a > 0). |
|
|
Соединим начало координат и точку Х прямой и отложим на ней отрезок длиной |ОY| = |a| |ОХ| в направлении X, если a > 0, или в противоположном направлении, если a < 0.
Советуем вам самостоятельно убедиться в том, что введенны е нами операции обладают следующими свойствами:
à) α(X + Y) = αX + αY; |
ä) 1X = Õ; |
á) (α + β)X = αX + βX; |
å) (–1)Õ = –Õ; |
â) α(βX) = (αβ)X; |
ж) если m — натуральное число, |
ã) 0Õ = O; |
òî mÕ = X + X+...+X. |
|
1 4 4 2 4 4 3 |
|
m ðàç |
Если в «обычном» пространстве к каким-либо точкам X, Y, Z прибавить одну и ту же точку С, то точки X′ = Õ + Ñ, Y′ = Y + C, Z′ = Z + C сохранят взаимное расположение исходных точек X, Y, Z и лишь переместятся в направлении отрезка ОС на расстояние, равное длине этого отрезка (рис. 3). Таким образом может быть определена операц ия параллельного переноса некоторого множества (фигуры): перенос — это прибавление ко всем элементам множества одного и того же эле ментаС.
Если же все элементы некоторого множества умножить на одн о и то же число, то мы получим фигуру, подобную исходной и распо ложенную «подобным образом». Такое преобразование в геомет рии называется гомотетией с центром О и коэффициентом a (ðèñ. 4).
Введенные выше операции над элементами пространства бла г имеют смысл при любой размерности пространства; это позво ляет нам использовать соответствующие геометрические термин ы (перенос, гомотетия), понимая их как результаты соответствующи х арифметических действий.

580 Математическое приложение
Функции и поверхности в пространстве благ
Представьте себе, что в вашей комнате есть камин. В морозны й день у камина будет тепло, а у окна — холодно. В каждой точке ваше й комнаты будет какая-то температура. Мы можем считать темп ературу t функцией точки в пространстве вашей комнаты: t = j (X). Но можем ввести в комнате декартовы координаты и рассматривать те мпературу как функцию трех переменных—координат точки: t = j (x1,x2, x3). Между этими описаниями существует простое соответствие — точк а и ее координаты взаимно однозначно определяют друг друга.
Подобно этому, величину, зависящую от количеств различных благ, можно рассматривать и как функцию n переменных — количеств этих благ x1,x2,...,xn, и как функцию набора, т. е. точки в пространстве благ:
j (Õ) = j (x1,x2,...,xn).
Множество точек, в которых функция принимает одно и то же значение j (X) = а, называют поверхностью уровня функции. Поверхность уровня разделяет пространство на две части, в одно й из которых j (Х) < а, а в другой j (Х) > а. Если, например, функция j (Х) описывает количественную полезность наборов, то поверхн ость уровня содержит такие наборы, полезность которых равна одной и т ой же величине, т. е. она является поверхностью безразличия (в кардиналистском смысле). Позже мы обсудим свойства поверхностей бе зразли- чия, отказавшись от количественного представления полезности.
Особый интерес представляют линейные функции в простран - стве благ. Линейной будем называть функцию, имеющую вид
l(X) = b1x1 + b2x2 +...+bnxn. |
(5) |
Различным наборам коэффициентов b1,b2,...,bn соответствуют разные линейные функции.
Поверхность уровня линейной функции на плоскости — это прямая, описываемая уравнением
b1x1 + b2x2 = à.
В трехмерном пространстве — это плоскость, удовлетворяющая уравнению
b1x1 + b2x2 + b3x3 = à.
В пространстве n измерений поверхность уровня линейной функции также будем называть плоскостью, хотя она отличается от обычной плоскости тем, что имеет не два, а n – 1 измерений (плоскость, размерность которой на единицу меньше размер ности пространства, называют также гиперплоскостью).
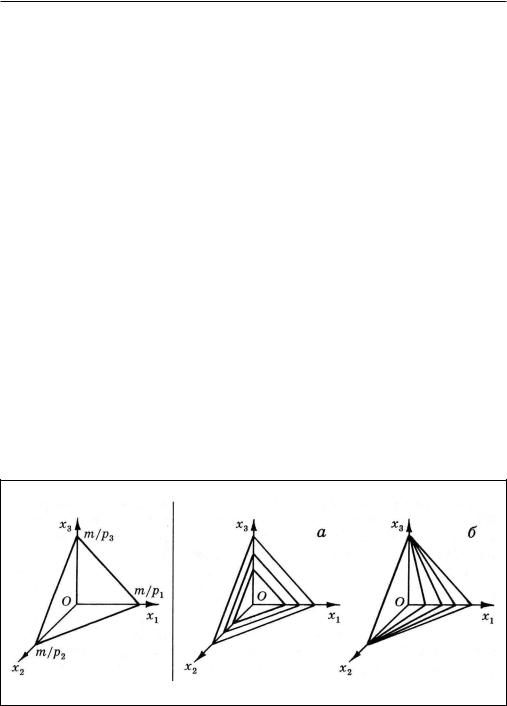
IV. Пространство благ 581
Åñëè öåíû p1, по которым приобретаются блага, не зависят от объемов покупок, то расходы на приобретение набора Х — линейная функция
s(X) = p1x1 + p2x2 +...+ pnxn.
Если m — денежный доход потребителя, то уравнение s(X) = m описывает его бюджетную плоскость — аналог бюджетной линии из лекции 14. Бюджетная плоскость отсекает от координатных ос ей отрезки длиной m/pi; ее положение в трехмерном пространстве показано на рис. 5. Покупательские возможности при доходе т описы-
ваются неравенством s(X) £ |
m вместе с неравенствами x1 ³ 0, |
x2 ³ 0, |
|
...,xn |
³ 0, выражающими неотрицательность объемов покупок. |
|
|
Из определения (5) следует, что всякая линейная функция обла- |
|||
äàåò |
свойствами |
|
|
|
l(X + Y) |
= l(X) + l(Y); |
(6) |
|
l(aÕ) = |
al(X). |
(7) |
Убедиться в этом вы можете самостоятельно.
Часто линейную функцию определяют как такую функцию, кото рая для любых точек Х и Y и любого числа a обладает свойствами (6) и (7). Можно доказать, что любая такая функция может быть представлена в виде (5), так ч то оба определения
эквивалентны.
Прямые и кривые
Допустим, что в момент времени t потребление некоторого человека определялось точкой X(t) в пространстве благ и с течением времени
Рис. 5. Бюджетная плос- |
Рис. 6. Изменение положения бюджетной плоско- |
кость в трехмерном |
сти при изменении дохода (а) и при изменении |
пространстве. |
цены 1-го продукта (б). |

582 Математическое приложение
изменялось. Тогда при изменении времени t от t0 äî t1 точка X(t) будет смещаться из положения Х(t0) в положение X(t1), прочертив в пространстве некоторую кривую. Этот пример показывает, каким образом могут задаваться различные кривые в пространстве благ. Если все координаты являются функциями одной и той же вещественной переменной
xi = xi(a), i = l,2,...,n,
то мы можем положение точки также рассматривать как значе ние функции того же параметра:
Õ(a) = (x1(a),x2(a),...,xn(a)).
И если параметр a принимает все значения из некоторого множества, например, интервала или всей числовой прямой (как гов орят, «пробегает» это множество), то переменная точка Х(a) «прочерчи- вает» некоторую кривую, конечную или бесконечную.
Прямые являются частным случаем кривых, и их можно задавать только что описанным способом.
Понятие прямой в n-мерном пространстве введем в два этапа. Возьмем произвольную точку В и воспользуемся рассмотренной выше операцией умножения вектора на число. Под прямой, про ходящей через начало координат О и точку В, будем понимать множество точек
Õ(a) = aÂ,
ãäå a пробегает всевозможные числовые значения. Если a принимает только неотрицательные значения, то точки Х(a) образуют луч, исходящий из начала координат и проходящий через точку В. А если a пробегает интервал [0, 1], то — отрезок, соединяющий О и В.
Для того чтобы получить прямую, не проходящую через начал о координат, можно взять прямую вида aВ и «сдвинуть» ее. Операцию параллельного переноса, или сдвига, некоторого множес тва мы также рассмотрели раньше: ей соответствует прибавление к о всем элементам множества одного и того же элемента пространст ва благ. Таким образом, множество точек вида
Õ(a) = À + a |
(8) |
образует некоторую прямую в пространстве благ. Так как Х(0) =А, Х(1) = А + В, эта прямая проходит через точки А и А + В. Если a принимает значения на отрезке [0, 1], то точки вида (8) располагаются на отрезке, соединяющем точки А и А + В.
Любые две точки пространства благ можно соединить прямой . Рассмотрим произвольные точки U и V. Положим в равенстве (8) А = U, А + В = V. Отсюда В = V – U, и мы получаем выражение для точек искомой прямой:
Õ(a) = U + a(V – U),
|
|
IV. Пространство благ |
583 |
|
|
|
|
|
|
èëè |
|
|
|
|
|
Õ(a) = (1 |
– a)U + aV. |
(9) |
|
Ïðè 0 £ a |
£ 1 точки вида (9) располагаются на отрезке, соединя- |
|||
ющем точки U и V. |
|
|
|
|
Отрезки |
в пространстве |
благ представляют особый интерес . Рас- |
||
смотрим два набора U и V и образуем из них «смесь», или «промежуточный» набор. Для этого возьмем долю a набора V и дополнительную долю (1 – a) набора U и соединим их вместе. Мы
получим набор, в который каждое |
из благ входит в количеств е |
wi = (1 − α)ui + αvi, |
i = 1,2,...,n. |
Таким образом мы получим набор W, лежащий на отрезке, соединяющем исходные наборы U и V. Смешивая исходные наборы в различных пропорциях, мы можем пройти весь отрезок UV.
Понятие отрезка позволяет придать строгий смысл слову «м ежду». Будем говорить, что набор W располагается между наборами U и V, если он располагается на отрезке UV, или, иными словами, если существует число a на интервале [0,1], такое, что W = (1 – a)U + aV.
Упражнение. Советуем вам убедиться в том, что наборы В, С, D, Е из табл. 1 лежат между наборами А и F. Найдите соответствующие значения параметра a.
Упражнение. Докажите теорему: если точки А и В принадлежат некоторой плоскости, то все точки прямой АВ расположены в этой плоскости.
|
|
|
|
|
|
Таблица 1 |
||
|
|
|
|
|
|
|
|
|
Номер |
|
|
Наборы |
|
|
Øàã |
|
|
|
|
|
|
|
|
|
||
продукта |
À |
B |
C |
D |
E |
F |
|
|
|
|
|||||||
|
|
|
||||||
|
|
|
|
|
|
|
|
|
1 |
0 |
40 |
50 |
60 |
70 |
80 |
10 |
|
2 |
40 |
35 |
30 |
25 |
20 |
15 |
–5 |
|
3 |
5 |
6 |
7 |
8 |
9 |
10 |
1 |
|
4 |
18 |
16 |
14 |
12 |
10 |
8 |
–2 |
|
|
|
|
|
|
|
|
|
|
Выпуклость
С понятием отрезка связано другое понятие — выпуклости. В Математическом приложении III было приведено определение выпуклого множества на плоскости. Теперь мы можем распростр а- нить его на пространство любой размерности:
множество точек называется выпуклым, если оно обладает

584 Математическое приложение
следующим свойством: отрезок, соединяющий любые две точки этого множества, целиком содержится в этом множестве.
Свойства выпуклых множеств, о которых говорится в упомяну - том приложении, имеют место и для выпуклых множеств в пространстве благ любой размерности, хотя некоторые формули ровки следует перевести с «плоского» на «n-мерный» язык. Например, плоскость разделяется на две части прямой, а рассматривае мое здесь пространство — гиперплоскостью. Остальные свойства могут быть перенесены без всяких изменений.
Предпочтения в пространстве благ
В лекции 13 обсуждается подход к описанию рационального поведения потребителя, не использующий количественного представления полезности и базирующийся лишь на способности потребителя сопоставить два любых набора благ и либо установит ь, какому из них отдать предпочтение, либо признать их равно ценными. Мы будем здесь использовать следующие символы для опи са-
íèÿ |
соответствующих |
отношений: |
||
À f  |
означает |
«À íå õóæå, ÷åì »; |
||
À f  |
— |
«А лучше, чем В»; |
||
À |
|
 |
— |
«А столь же привлекательно, как В». |
ã |
|
|
|
|
В дальнейшем будем использовать слова «улучшение», «ухуд - шение» и т. д. в смысле отношения предпочтения, которым руководствуется данный потребитель. В таком же значении будем говорить о «возрастании» и «убывании полезности», не вкладывая в эти выражения количественного смысла.
Сформулируем некоторые основные свойства потребительск их предпочтений, рассматривая их как отношения между элемен тами
пространства |
áëàã. |
1. Åñëè õi |
³ yi , i = 1, ...,n, òî Õ f Y. Åñëè ê òîìó æå Õ ¹ Y, òî |
Õ f Y. Ýòî |
свойство характеризует монотонность предпочтения п о |
каждой координате. Его называют ненасыщаемостью потребителя. 2. Если U p С p V, то на отрезке UV существует точка W, такая,
÷òî Wã С. Иными словами, если точки U и V расположены в различных частях, на которые пространство делится множес твом безразличия, то отрезок UV пересекает это множество. Это свойство характеризует непрерывность предпочтения.
Отмеченное свойство на первый взгляд кажется само собой р азумеющимся. Тем не менее существуют такие предпочтения, для которых о но не имеет места. Примером может служить так называемое лексикографическое (алфавитное) упорядочение:
Õ f Y, åñëè x1 > y1
èëè x1 = y1 è x2 > y2,

IV. Пространство благ 585
èëè x1 = y1, x2 = y2 è x3 > y3,
....
èëè x1 = y1, x2 = y2 ,...,xn–1 = yn–1 è xn > yn.
На рис. 7 выделено множество элементов, предпочтительных по отношению к С: это полуплоскость, расположенная правее С, и луч над С. Каждое множество безразличия при этом состоит из единственной точки.
Непрерывность — чрезвычайно важное свойство предпочтения. Из него, в частности, следует существование функции полезности u(Х), значения которой согласованы с предпочтениями: u(Х) > u(Y) тогда и только тогда, когда Х f Y.
Постарайтесь доказать это утверждение самостоятельно, последовательно рассмотрев следующие положения.
Пусть В — вектор, все компоненты которого положительны, a R — луч, состоящий из точек вида aÂ, a ³ 0.
1) для любого Х с неотрицательными компонентами на луче найдутся точки U,
V, такие, |
÷òî U p Õ p V; |
ã |
X. Иными словами, луч R |
||
2) |
íà |
луче R найдется точка W, такая, что W |
|||
пересекает все множества |
безразличия; |
|
|
||
3) |
построим функцию |
u(Х) следующим образом. Возьмем такое число a, ÷òî |
|||
Õã a В (в силу п. 2 для любого Х такое число обязательно найдется). Положим u(Х) = a;
4) |
åñëè a > b, òî a  f b В, и обратно; |
5) |
если u(Х) > u(Y), то Х f Y, и обратно, т. е. построенная в п. 3 функция есть |
функция полезности.
Если существует хотя бы одна функция полезности, то их сущ е- ствует бесконечно много: если j (u) — монотонно возрастающая функция, то u*(Õ) = j (u(Х)) — также функция полезности.
Непрерывность — существенное условие существования фун кции полезности. Если бы предпочтение не было непрерывным, то ф ункция полезности могла бы не существовать. Доказано, например, ч то для лексикографического упорядочения не существует функция полезности.
Существование функции полезности позволяет утверждать, что множество безразличия — это множество, удовлетворяющее урав нению u(Х) = с, где с — константа. Иными словами, множество безразличия — это поверхность уровня функции полезности. Поэтому в даль нейшем мы
ñполным правом можем говорить о поверхности безразличия.
3.Отказ от количественного измерения полезности требует заменить закон убывающей предельной полезности (поскольку она так же неизмерима) таким допущением о предпочтениях, которое так же согла-
совывалось бы с наблюдаемыми эффектами поведения потреб ителя.
