
UMK_po_mikroekonomike / 50_лекций по микроэкономике / 50_V. Задача Лагранжа
.pdf
V. Задача Лагранжа 587
одного вида, а взятые в некотором количестве наборы V — как благо второго вида; назовем их «комплектное благо 1» и «комплект ное благо 2». Теперь обсуждаемое допущение можно сформулировать сле дующим образом: при замене любого комплектного блага любым други м норма замещения убывает с увеличением объема замещаемого благ а.
Рассмотрим множество Ω наборов, включающих только комплектные блага 1 и 2 в произвольных количествах. Все такие наборы имеют вид Х = β1U + β2V, ãäå β 1 è β2, — неотрицательные числа, выражающие количества комплектных благ. Отрезок UV состоит из точек вида (1 – a)U + aV, причем a ³ 0 è 1 – a ³ 0, так что отрезок UV целиком содержится в множестве Ω . Но множество Ω — это двухпродуктовое пространство, в котором существуют только комплектные блага 1 и 2. А мы уже знаем, что в двухпродуктовом пространстве закон убыва ющей предельной полезности имеет своим следствием тот факт, что н аихудшая точка любого отрезка лежит на его конце.
Возьмем теперь в пространстве благ какую-либо поверхност ь безразличия и точку С на ней. Пусть U f C и V f C, a точка Х расположена на отрезке UV. Тогда обязательно имеет место отношение Х f С — ведь наихудшая точка отрезка UV — это U или V.
Таким образом, если U и V принадлежат множеству точек, не уступающих точкам данной поверхности безразличия, то и ве сь отрезок UV также принадлежит этому множеству. А это означает, что закон убывающей предельной полезности в пространств е благ любой размерности «выглядит» точно так же, как и в простра нстве двух благ: множество наборов, не менее предпочтительных, ч ем лежащие на данной поверхности безразличия, выпукло.
V. Задача Лагранжа
Безусловный и условный экстремумы
Важное место в математическом аппарате экономики занима ют оптимизационные задачи — задачи, в которых ищется наилучш ее в определенном смысле решение. В экономической практике т ребуется использовать имеющиеся ресурсы наиболее выгодны м образом. В экономической теории одним из отправных пунктов яв ляется постулат о том, что каждый экономический субъект, име я определенную свободу выбора своего поведения, отыскивае т наилуч- ший со своей точки зрения вариант. И оптимизационные зада чи служат средством описания поведения экономических субъ ектов, инструментом исследования закономерностей этого поведе ния.
Многие задачи оптимизации формулируются следующим обра зом. Решение, которое должен принять субъект, описывается набо ром чисел

588 Математическое приложение
x1,x2,...,xn (или точкой Х = (x1,x2,...,xn) n-мерного пространства). Достоинства того или иного решения определяются значениям и функции f(X) = f(x1,x2,...,xn) — целевой функции. Наилучшее решение — это такая точка X, в которой функция f(X) принимает наибольшее значение. Задача нахождения такой точки описывается следующим образом:
f(X) ® max.
Если функция f(X) характеризует отрицательные стороны решения (ущерб, убытки и т. п.), то ищется точка X, в которой значение f(X) минимально:
f(X) ® min.
Минимум и максимум объединяются понятием экстремума. Для определенности мы в этой статье будем говорить только о задачах максимизации. Поиск минимума не требует специаль ного рассмотрения, поскольку заменой целевой функции f(X) на –f(X) всегда можно «превратить недостатки в достоинства» и све сти минимизацию к максимизации.
Из каких вариантов должен быть выбран наилучший? Иными сл овами, среди каких точек пространства нужно искать оптимум? О твет на этот вопрос связан с таким элементом оптимизационной задачи, к акмножество допустимых решений. В некоторых задачах допустимыми являются любые комбинации чисел x1,x2,...,xn, т. е. множество допустимых решений — это все рассматриваемое пространство.
В других задачах следует принимать во внимание различные ограничения, означающие, что не все точки пространства доступны при выборе. В содержательных постановках задач это может быть связано, например, с ограниченностью располагаемого количеств а ресурсов.
Ограничения могут быть представлены в форме равенств вид а
g(X) = 0
или неравенства
g(X) ³ 0.
Если условия имеют несколько другую форму, скажем, g1(X) = g2(X) èëè g(X) £ А, то их можно привести к стандартному виду, перенеся все функции и константы в одну из частей равенства или нер авенства.
Экстремум, отыскиваемый во всем пространстве, без какихлибо ограничивающих условий, носит название безусловного. Если целевая функция непрерывно дифференцируема, то, как извес тно из общего курса математического анализа, необходимое услов ие безусловного экстремума функции состоит в равенстве нулю всех ее частных производных:
∂f |
= 0, i = 1,...,n |
(1) |
|
||
∂xi |
|
|

V. Задача Лагранжа 589
(для упрощения записи мы иногда будем опускать обозначен ия аргументов).
Если же заданы ограничения, то экстремум ищется лишь сред и точек, которые удовлетворяют всем ограничениям задачи, та к как только такие точки являются допустимыми. В этом случае эк стремум носит название условного.
Чрезвычайно полезным средством экономического анализа ока-
залась задача |
поиска условного |
экстремума: |
|
f(X) ® max |
(2) |
при условиях |
|
|
g1(X) = 0; g2(X) = 0; ...gn(X) = 0,
все ограничения которой представляют собой равенства.
Если при этом целевая функция и все ограничивающие функции непрерывно дифференцируемы, то такую задачу мы будем называть задачей Лагранжа.
Задача Лагранжа с одним ограничением
В настоящем пункте будет рассмотрена задача, имеющая след у- ющую структуру:
f(X) ® max |
(3) |
при условии |
|
g(Õ) |
= 0. |
Для иллюстрации некоторые авторы приводят такой пример. П о склону горы идет дорога, требуется найти на ней самую высо кую
точку. На рис. 1 представлена |
|
карта местности с нанесенными на |
|
нее линиями равных высот; синяя |
|
линия — это дорога. Точка М, в |
|
которой дорога касается одной из |
|
линий уровня, — это и есть наи- |
|
высшая точка дороги. |
|
Åñëè Õ = (x1, x2) — точка плос- |
|
кости, x1 è x2 — ее координаты, то |
|
задаче можно придать следующую |
|
форму. Пусть f(X) — высота точ- |
|
ки Х над уровнем моря, а уравне- |
|
ние g(X) = 0 описывает дорогу. |
|
Тогда наивысшая точка дороги — |
|
решение задачи (3). |
Рис. 1. Задача о дороге на склоне |
|

590 Математическое приложение
Если бы дорога проходила через вершину горы, то ее высшая точка была бы самой высокой точкой местности, и ограничен ие можно было бы не принимать во внимание.
Если же дорога не проходит через вершину, то, немного уклон ившись от дороги, можно было бы подняться выше, чем двигаясь с трого по дороге. Отклонение от дороги соответствует попаданию в такие точки, где g(X) ¹ 0; при малых отклонениях достижимую при этом высоту можно приближенно считать пропорциональной откл онению.
Идею решения задачи Лагранжа можно представить следующим образом: можно попытаться «исправить» рельеф местности так, чтобы отклонение от дороги не давало преимуществ в достижении высоты. Для этого нужно заменить высоту f(X) функцией
L(X) = f(X) – lg(X),
где множитель l подбирается таким образом, чтобы участок склона в окрестности точки М стал горизонтальным (слишком малое значение l не устранит преимуществ отклонений от дороги, а слишком большое — придаст
преимущества отклонениям в противоположную сторону). Теперь, поскольку рельеф L(X) делает площадку в окрестности
точки оптимума горизонтальной, эта точка удовлетворяет р авенствам
∂L |
= 0, |
∂L |
= 0, |
|
∂x |
∂x |
|||
|
|
|||
1 |
|
2 |
|
а так как точка лежит на дороге, то — и ограничению g(X) = 0. Пример с горой и дорогой — лишь иллюстрация идеи; точно так же двумерный случай использован исключительно для на глядности. Подобным образом можно было бы рассуждать и в общем ,
n-мерном случае.
Справедливо следующее утверждение:
Åñëè f(x1,...,xn) è g(x1,...,xn) —непрерывно дифференцируемые функции всех своих аргументов, то решение задачи
f(x1,...,xn) ® màõ
при условии
g(x1,...,xn) = 0
|
|
V. Задача Лагранжа |
591 |
|
|
|
|
удовлетворяет равенствам |
|
||
|
∂L |
= 0, i = 1,...,n; |
(4) |
|
|
||
|
∂xi |
|
|
|
|
∂L = 0, |
(5) |
∂λ
ãäå
L(x1,...,xn;λ)= f(x1,...,xn ) − λg(x1,...,xn ).
Функция L(X; l) получила название функции Лагранжа (или лагранжиана) задачи (3), а коэффициент l — множителя Лагранжа.
Заметим, что равенство (5) — это представленное в другой форме ограничение g(X) = 0.
Приведенные выше рассуждения, разумеется, не являются док азательством сформулированного здесь утверждения; они лишь помогают понять существо метода: составляющая lg(X) в составе функции Лагранжа должна уравновешивать возможное увеличение ма ксимального значения функции f(X) при малом отклонении (на единицу) значений функции g(X) от нуля. Это обстоятельство в дальнейшем будет весьма полезно при обсуждении смысла множителя Лаг ранжа.
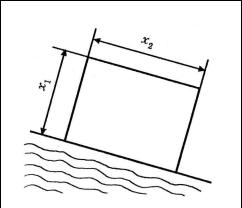
Рассмотрим чрезвычайно простой пример. Веревкой длины А требуется огородить на берегу моря прямоугольный участо к наибольшей площади (берег считается прямолинейным).
Это один из вариантов так называемой задачи Дидоны. Дидон а, сестра тирского царя, — легендарная основательница и первая властительни ца Карфагена. Покинув родину и прибыв в Северную Африку, она купила у местных жит елей прибрежный участок, который, по условию, можно огородить воловьей шку рой. Разрезав шкуру на тонкие ремешки, она связала из них тонкую веревку. Остал ьное — геометрическая задача: огородить участок наибольшей возможной площади.
Обозначим |
стороны прямоу- |
||
гольника x1 è x2 (рис. 3). Решим |
|||
сначала задачу без использова- |
|||
ния метода Лагранжа. |
|
|
|
Очевидно, x2 |
= À — 2x1, è ïëî- |
||
щадь прямоугольника равна S = |
|||
= x1x2= x1(A — |
2x1). Рассматривая |
||
ее как функцию одного аргумента x1, |
|||
нетрудно найти его значение, при |
|
||
котором площадь максимальна: x1 |
= |
|
|
= A/4. Отсюда x2 |
= А/2. Максималь- |
|
|
|
|||
ная площадь равна S* = A2/8. |
Рис. 3. К задаче Дидоны. |
||
|
|
||

592 Математическое приложение
Теперь рассмотрим эту же задачу в форме задачи Лагранжа: x1x2 ® màõ
при условии
2x1 + x2 – А = 0. Лагранжиан этой задачи равен
L(x1,x2;l) = x1x2 — l(2x1 + x2 – A),
и условия экстремума имеют вид
∂L |
= x − 2λ = 0, |
∂L |
= x − λ = 0, |
|
|
||
∂x1 |
∂x2 |
||
2 |
1 |
||
òàê ÷òî
x2 = 2l,
x1 = l,
2x1 +x2 = A.
Подставляя значения x1 è x2 из первого и второго равенств в третье, находим, что 4l = А, откуда
l = À/4; x1 = À/4; x2 = À/2,
как и при решении первым способом.
Этот пример показывает распространенный способ решения задачи Лагранжа. Соотношения (4) и (5) образуют систему уравнений от носительно x1,..., xn è l. Система состоит из n + 1 уравнения — n уравнений вида (4) и одно уравнение вида (5). Число уравнений равно числ у неизвестных. Из уравнений вида (4) можно попытаться выразить ка ждую из неизвестных x1,...,xn через l, т. е. решить ее как систему из n уравнений, рассматривая l как параметр. Подставляя получившиеся выражения в уравнение (5) — напомним, что оно совпадает с ограничением, — получаем уравнение относительно l. Решая его, находят l, после чего определяются исходные неизвестные x1,...,xn.
Смысл множителей Лагранжа
При решении задачи Лагранжа мы интересовались значениям и x1,...,õn; кроме того, нас могло интересовать экстремальное значен ие целевой функции f(X). Но в процессе решения попутно было определено значение еще одной величины — множителя Лагранжа.
Оказывается, множитель Лагранжа — весьма существенная ха рак-

V. Задача Лагранжа 593
теристика решаемой задачи. Чтобы смысл ее стал яснее, неск олько изменим формулировку ограничения, ничего не изменяя по су ществу.
Типичная экономическая ситуация характеризуется тем, чт о приходится искать наиболее выгодное решение при ограниченн ом количестве некоторого ресурса. Если r — заданное количество ресурса, а функция h(X) характеризует потребное его количество для достижения точки X, то ограничению естественно придать форму
h(X) £ r.
По характеру задачи часто бывает ясно, что для достижения оптимума ресурс нужно использовать полностью, так что огранич ение может быть записано в виде равенства
h(X) = r. |
(6) |
Формально это условие можно представить в стандартной фо рме g(X) = = h(X) – r = 0. Но значительный интерес представляет максимально достижимый уровень функции f(X) в зависимости от имеющегося количества ресурса r. Обозначим
F(r) = max{f(X) | h(X)=r}.
В правой части — принятое обозначение условного экстремума: после вертикальной черты выписывается условие.
Вспомним, что при обсуждении структуры лагранжиана мы интерпретировали lg(X) как составляющую, уравновешивающую возможный прирост максимума f(X) при отклонении g(X) от нуля. Но отклонение g(X) от нуля есть отклонение h(X) от r. Если располагаемое количество ресурса получает приращение r , то мы должны ожидать приращение максимума функции f(X) на l r .
В действительности это соотношение носит приближенный х а-
рактер. Точный результат мы получили бы в пределе при |
r → 0: |
||
|
dF(r) |
= λ. |
(7) |
|
dr |
||
|
|
|
|
Таким образом, множитель Лагранжа характеризует скорост ь изменения максимума целевой функции при изменении огранич ивающей константы r в ограничении вида (6).
В рассмотренном в предыдущем пункте варианте задачи Дидоны ограниченным ресурсом была длина веревки А. Максимальная площадь оказалось равной S(A) =A2/8. Отсюда dS(A)/dA = A/4:, что
âточности соответствует найденному при решении значени юl. Приведем еще одно рассуждение в пользу такой трактовки
множителя Лагранжа. Для всевозможных точек Х найдем значе- ния f(X) и h(X) и отложим эти значения в виде точек в декартовых
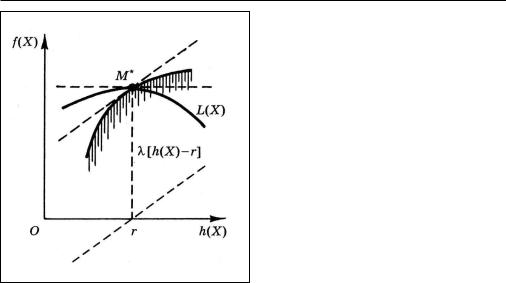
594 Математическое приложение
координатах (рис. 4). Если при каждом значении h(X) существует максимум функции f(X), то все точки расположатся ниже некоторой кривой, показанной на рисунке жирной линией.
Нас интересуют точки, соответствующие условию h(X) = r. Максимум f(X) помечен точкой М*; обозначим l наклон кривой в этой точке. Если в качестве ординаты брать не f(X), a L(X; l) = f(X) – – l[h(X) – r], то новая верхняя граница (синяя кривая) имела бы в точке М* горизонтальную касательную. Это значит, что в исходном n- мерном пространстве соответствующая точка М — стационарная точка функции L(X; l) с данным
значением параметра X. Таким образом, l — множитель Лагранжа. Но жирная черная кривая — это график функции F(r), a l —
его угловой коэффициент, откуда и следует равенство (7).
Рацион Робинзона
Обратимся теперь к задаче о потреблении примерно в таком виде, в каком ее ставил Госсен.
Человек может потреблять блага n видов в количествах xi, i = 1,...,n. Общая полезность потребления i-того блага описывается функцией TUi(xi). Предельная полезность MUi(xi) = dTUi (xi)/dxi убывает с ростом xi — в этом состоит закон Госсена. Полезность потребления всех благ суммируется по отдельным благам, та к что
TU(X) = åTUi (xi ).
i
Будем считать, опять-таки следуя Госсену, что потребитель ские возможности человека ограничены лишь временем, которое он мо жет затрачивать на добывание и потребление благ, как это имело место у Робинзона Крузо. Если на единицу i-того блага ему приходится тратить ti единиц времени, то ресурсное ограничение выражается равенством
åtixi = T, |
(8) |
i |
|
где Т — фонд времени, выделяемый на потребление благ.

V. Задача Лагранжа 595
Задача рационального потребления теперь сводится к опре делению такого «рациона» — набора благ Х = (x1,...,xi), —который доставляет максимум TU(X) при ограничении (8).
Лагранжиан этой задачи:
|
|
|
|
é |
ù |
|
L(X;l) = åTUi(xi ) - lêåtixi |
- Tú. |
|||
|
|
i |
|
ë i |
û |
Условия оптимума выражаются |
системой |
|
|||
|
¶L |
= MU (x ) - lt = 0, i = 1,...n, |
|||
|
|
||||
|
|
i |
i |
i |
|
|
¶xi |
|
|
|
|
èëè |
|
|
|
|
|
|
MUi(xi) = |
l ti, |
i = l,...,n. |
(9) |
|
Итак, предельные полезности различных благ в точке оптимума пропорциональны удельным затратам времени. Это значит, чт о для любой пары благ (i,j) отношение их предельных полезностей равно отношению удельных затрат времени:
MUi (xi ) = ti .
MUj (xj ) tj
А отсюда следует, что дополнительная малая порция времени (скажем, минута), затрачиваемая на любое из благ, дает один и тот же прирост полезности.
Величина этого прироста, как это следует из результата пр еды-
дущего |
пункта, определяется коэффициентом l: если Робинзон |
|||
сможет |
выделить на потребление благ дополнительно |
DT единиц |
||
времени, то общая полезность |
возрастет при этом на |
величи ну |
||
|
TU |
≈ λΔ |
T. |
(10) |
|
|
|
||
Заметим, что убывание предельной полезности гарантирует единственность оптимума. Если взять другие значения xi (обозначим их xi′ ), также удовлетворяющие условиям пропорциональности пре - дельных полезностей удельным затратам времени:
MUi (xi′) = λi′ti,
то либо l¢ > l, и тогда xi′ < xi для всех продуктов (предельная полезность убывает с ростом хi); ëèáî λ′ < λ — и тогда xi′ > xi äëÿ âñåõ i. Â

596 Математическое приложение
первом случае потребное количество времени меньше T, во втором — больше, но ни в одном из них ограничение не будет выполнено .
Таблица 1 |
Попутно отметим следующее |
обстоя- |
тельство. Система уравнений (9) |
опреде- |
|
Данные к задаче |
ляет наилучший набор благ при любом |
|
о рационе Робинзона |
фиксированном количестве Т выделенно- |
|
i |
ai |
ti |
|
|
|
1 |
50 |
1 |
2 |
100 |
2 |
3 |
50 |
2 |
|
|
|
го времени; с величиной Т связано лишь численное значение l. Считая величину Т переменной, введем как в предыдущем пункте, функцию
ì |
|
ü |
F(T) = maxíTU(X)|åtixi = Tý, |
||
î |
i |
þ |
которую можно трактовать как общую полезность времени. Это — «вторичная» полезность: ее величина определяется максим альной полезностью набора благ, достижимой при данном количеств е выделенного времени. Точный смысл приближенного равенства (10) состоит в том, что
dF(T) = λ, dT
ò. å. l — предельная полезность времени для Робинзона.
Как мы только что видели, сравнивая l è λ′ для различных наборов благ, чем больше Т, тем меньше l, Поскольку природа выделяемого ресурса несущественна, мы можем сделать след ующий общий вывод:
если предельная полезность каждого блага снижается с рос том объема его потребления, а затраты ресурса пропорциональн ы объему, то предельная полезность ресурса падает с увеличением коли- чества используемого ресурса.
Проиллюстрируем эти результаты числовым примером. Допустим, что Робинзон потребляет 3 вида благ, причем все частны е функции полезности имеют один и тот же вид
TUi(xi) = àiln(xi + 1)
с различными коэффициентами ai. Он может выделить на потребление 15 ч в сутки; остальные данные приведены в табл. 1. Воспользуемся системой (9):
MUi (xi ) = |
ai |
|
= lti, i = 1, 2, 3. |
||
xi + 1 |
|||||
|
|
|
|||
Отсюда |
|
|
|
|
|
|
xi = |
ai |
- 1. |
||
|
lt |
||||
|
|
|
|
||
|
|
|
i |
|
|
