
UMK_po_mikroekonomike / 50_лекций по микроэкономике / 50_VII. Математика производственных функций
.pdf
VII. Математика производственных функций 605
f(x) = lim f(x |
) = lim kx |
= k lim x = kx, |
||
n→∞ |
n |
n→∞ |
n |
n→∞ n |
чем и исчерпывается доказательство.
2. Полученный результат может быть использован и при решен ии некоторых других функциональных уравнений, в частности, т ого, которое возникло в связи с условием согласованности во врем ени:
k(T1 + T2) = k(T1)k(T2), |
(2) |
причем неизвестная функция здесь должна принимать положительные значения.
Почленно логарифмируя функциональное уравнение (2) lnk(T1 + T2) = lnk(T1) + lnk(T2),
мы убеждаемся в том, что функция L(T) = lnk(T) аддитивна:
L(T1 + T2) = L(T1) + L(T2),
и в силу только что доказанного свойства аддитивных функц ий L(T) = = bT. Итак, мы видим, что lnk(T) = bT и, следовательно, решением интересующего нас уравнения является
k(T) = eβ T.
Этот результат и был использован при построении функции р оста.
VII. Математика производственных функций
Эластичность производственной функции и отдача от масшт аба
В настоящем пункте мы несколько раз будем ссылаться на Математическое приложение II, которое для краткости будем обозначать МП II.
Как указывалось в лекции 22, предельный продукт некоторого ресурса характеризует абсолютное изменение выпуска продукта, приходящегося на единицу изменения расхода данного ресу рса, причем изменения предполагаются малыми. Для производств енной функции q = = f(x1, ..., xn) предельный продукт i-того ресурса равен частной производной:
MPi = ∂f .
∂xi

606 Математическое приложение
Влияние относительного изменения расхода i-го фактора на выпуск продукта, представленное также в относительной форме, характеризуется частной эластичностью выпуска по затратам этого продукта:
Ε |
|
[f] = |
¶f |
× xi |
|
¶xi |
|||
x |
|
f |
||
|
i |
|
||
|
|
|
|
|
(см. МП II). Для простоты будем обозначать Εxi [f] = ei.Частная эластичность производственной функции равна отношению предельного продукта данного ресурса к его среднему продукт у.
Рассмотрим частный случай, когда эластичность производс твенной функции по некоторому аргументу — постоянная величин а. Если по отношению к исходным значениям аргументов x1, x2, ..., xn один из аргументов (i-тый) изменится в l раз, а остальные останутся на прежних уровнях, то изменение выпуска продук та описывается степенной функцией:
q = Alei
(см. МП II, формула (8) и упражнение 3). Полагая что А = f(x1, ..., xn), и поэтому
q = lei f(x1,...,xn ).
l = 1, найдем,
(1)
В общем случае, когда эластичность — переменная величина, равенство (1) является приближенным при значениях l, близких к единице, т. е. при l = 1 + e, и тем более точным, чем ближе e| |ê íóëþ.
Пусть теперь затраты всех ресурсов изменились пропорционально, т. е. затраты каждого изменились в l раз. Последовательно применяя только что описанный прием к x1, x2, ..., xn, можно убедиться в том, что теперь
q » λe1λe2 ×...×λenf(x1,...,xn ),
èëè
f(λx1,λx2,...,λxn ) » λe1+e2 +...+enf(x1,x2,...,xn ).
Сумма частных эластичностей некоторой функции по всем ее аргументам получила название полной эластичности функции. Вводя обозначение
E = åei
i
для полной |
эластичности производственной функции, мы мож ем |
||||||||||||
представить |
полученный |
результат |
â |
âèäå |
|
|
|
|
|||||
|
f(λx |
,λx |
,..., |
λx |
n |
) ≈ λEf(x ,x |
,...,x |
n |
). |
(2) |
|||
|
1 |
2 |
|
|
|
1 |
2 |
|
|
|
|
||
Равенство (2) показывает, что |
полная |
эластичность |
производ - |
||||||||||

VII. Математика производственных функций 607
ственной функции позволяет дать отдаче от масштаба число вое выражение. Пусть расход всех ресурсов немного увеличился с сохранением всех пропорций (l > 1). Если Е > 1, то выпуск продукции увеличился больше, чем в l раз (возрастающая отдача от масштаба), а если Е < 1, то меньше, чем в l раз. При Е = 1 выпуск продукции изменится в той же самой пропорции, что и затрат ы всех ресурсов (постоянная отдача).
Выделение короткого и длительного периодов при описании характеристик производства — грубая схематизация. Изменение объемов по требления различных ресурсов — энергии, материалов, рабочей силы, станков, зданий и т. д. — требует различного времени. Допустим, что ресурсы перенумерованы в порядке убывания подвижности: быстрее всего можно изменить x1, затем x2 и т. д., а изменение xn требует наибольшего времени. Можно выделить сверхкоротк ий, или нулевой, период, когда не может измениться ни один фактор; 1-й период, когда и зменяется только x1; 2-й период, допускающий изменение x1 è x2 и т. д.; наконец, длительный, или n- й период, в течение которого могут измениться объемы всех ресурсов. Различных периодов, таким образом, оказывается n + 1.
Рассматривая некоторый промежуточный по величине, k-й период, мы можем говорить о соответствующей этому периоду отдаче от масшт аба, имея в виду пропорциональное изменение объемов тех ресурсов, которые в э том периоде могут изменяться, т. е. x1, x2, ..., xk. Объемы xk + 1, xn, при этом сохраняют фиксированные значения. Соответствующий этому периоду показатель отда чи от масштаба равен
e1 +å2 + ...+åk.
Удлиняя период, мы добавляем к этой сумме следующие слага емые, пока не получится значение Е для длительного периода.
Поскольку производственная функция возрастает по каждо му аргументу, все частные эластичности е1 положительны. Отсюда следует, что чем продолжительнее период, тем больше отдача от масштаба.
Однородные производственные функции
Равенство (2) является приближенным при l, близком к единице. Функции, для которых при любых l и любых x1, x2,..., xn выполняется равенство
f(λx1,λx2,...,λxn ) = λαf(x1,x2,...,xn ),
получили название однородных функций, а величина a — степени однородности. Однородные функции 1-й степени называют линейно однородными. Ниже приведены примеры однородных функци й; в квадратных скобках указаны степени однородности:
y = a x |
+ a x |
+ a x |
[1]; |
y = a |
x1 |
+ a |
x2 |
|
[0]; |
|||||
x |
|
|
|
|||||||||||
1 |
1 |
|
2 |
2 |
3 3 |
|
1 |
|
2 x |
|
|
|||
|
|
|
|
|
|
|
|
3 |
|
|
3 |
|
|
|
y = a x2 |
+ a x x |
[2]; |
|
|
|
|
|
|
|
|
||||
1 |
1 |
|
2 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
0.2 |
0.5 |
|
|
|
|
x1 |
|
|
x2 |
|
|
||
y = a1x1 |
|
x2 |
|
|
[0.7]; |
y = a1 |
|
+ a2 |
|
[–1]. |
||||
|
|
|
x x |
x x |
||||||||||
|
|
|
|
|
|
|
|
2 |
3 |
|
1 |
3 |
|
|
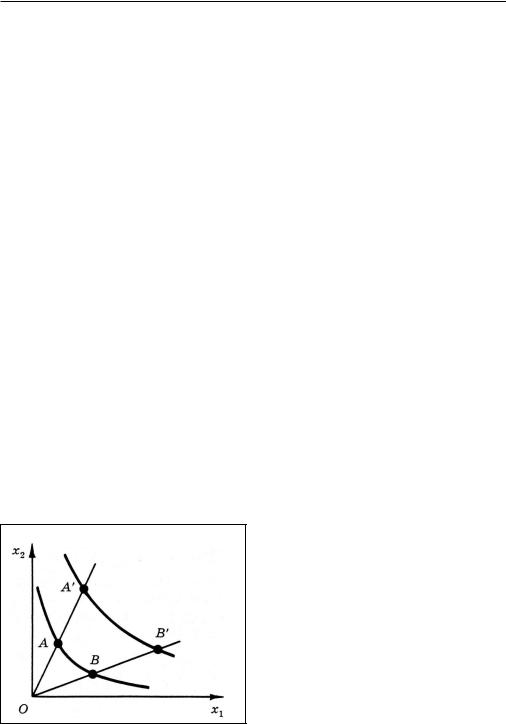
608 Математическое приложение
Функции у = а + b1x1 + b2x2 è ó = b1x1 + b2 x22 неоднородны. Однородная функция степени a удовлетворяет уравнению Эйлера:
å |
¶f |
xi |
= af. |
(3) |
|||
¶x |
|||||||
i |
|
i |
|
|
|
|
|
Разделив обе части уравнения Эйлера на |
f, получим |
||||||
å |
¶f |
|
xi |
|
|||
|
× |
|
= E = a. |
|
|||
¶x |
f |
|
|||||
i |
|
|
i |
|
|
|
|
Таким образом, общая эластичность однородной функции — постоянная величина. При этом частные эластичности по каж дому аргументу могут быть переменными.
Однородные функции обладают многими свойствами, делающи - ми их весьма привлекательными для приближенного описани я реальных производственных объектов.
Пропорциональному изменению всех аргументов геометриче ски соответствует движение вдоль луча, выходящего из начала коо рдинат. Возьмем две любые точки, лежащие на одной изокванте, скаже м,А и В (рис. 1). Проведем из начала координат лучи через эти точки и
отложим на них точки A′ è B′ так, чтобы каждый из отрезков |
OA′ |
è OB′ áûë â l раз длиннее соответствующего отрезка ОА или |
ÎÂ. |
Если исходной изокванте соответствовало значение произ водственной функции q, то и точке A′ то и точке B′ соответствует одно и то же значение lα q, так что точки A′ è B′ лежат на одной изокванте. Отсюда следует, что любая изокванта однородной производс твенной функции может быть получена из любой другой с помощью пре образования подобия (гомотетии) с центром в начале координа т.
Рассмотрим произвольную производственную функцию. Возьмем на различных изоквантах точки, в которых наклон изоквант один и тот же. Соединяющая эти точ- ки линия называется изоклиной (от греч. klinw — наклонять). Иными словами, изоклина объединяет производственные варианты, характеризующиеся одинаковыми значениями предельной нормы технической замены ресурсов. Как отмечалось в разделе 2 лекции 22, линия оптимального роста фирмы характеризуется по-
VII. Математика производственных функций 609
стоянством предельной нормы замены, которая во всех точка х этой линии равна отношению цен ресурсов. Таким образом, линия р оста
— это одна из изоклин производственной функции. При измен ении цен ресурсов фирма «перескакивает» с одной изоклины на др угую.
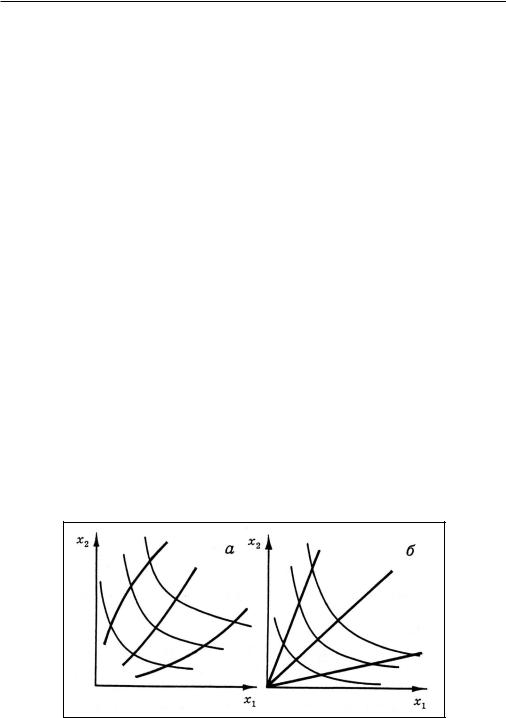
Из подобия изоквант однородной функции следует, что в точ ках одного луча, выходящего из начала координат, все изоквант ы имеют один и тот же наклон. Таким образом, все изоклины однородно й производственной функции (и, в частности, линия оптимальн ого роста) — лучи, выходящие из начала координат (рис. 2,б).
Однородность производственной функции существенно упро щает анализ отдачи от масштаба. Прежде всего степень однородно сти характеризует влияние масштаба затрат ресурсов на выпуск п родукции при любых изменениях масштаба (а не только при малых, как о бщая эластичность произвольной функции). Не менее важно и то об стоятельство, что изменение масштаба выпуска продукции в случ ае однородной производственной функции происходит путем пропо рционального изменения расхода ресурсов, поскольку в этом случае такой характер изменения отвечает линии оптимального роста фи рмы.
Функция Кобба—Дугласа
Трудно было бы ожидать, чтобы такой сложный объект, как производство, можно было описать функцией, имеющей просто е аналитическое выражение. Однако для того чтобы производс твенную функцию можно было использовать не только для получен ия тех или иных теоретических утверждений, но и для выполнен ия конкретных расчетов, она должна иметь форму, допускающую количественную оценку. Как и в других областях знания, уси лия ученых были направлены на отыскание таких функций, которы е
Рис. 2. Семейства изоклин производственных функций общего вида (а) и однородной (б).

610 Математическое приложение
позволили бы с достаточной точностью описать характерис тики реальных производственных объектов и исследовать их сво йства.
В 1928 г. К. У. Кобб и П. X. Дуглас для описания зависимости объема продукции отрасли от затрат труда (L) и капитала (K) предложили следующую функцию:
q = ALαL KαK . |
(4) |
До настоящего времени функция Кобба—Дугласа наряду с нек о- торыми другими широко используется для приближения прои зводственных функций различных объектов. В более общем случае функцией Кобба—Дугласа называют функцию
q = Axα1xα2 |
...xαn. |
(5) |
1 2 |
n |
|
Функция Кобба—Дугласа — степенная функция всех своих аргументов; ее частные эластичности еi, постоянны и совпадают с параметрами αi . Это однородная функция степени
α = α1 + α2 +...+ αn,
так что сумма показателей степени в функциях (4) или (5) служи т показателем отдачи от масштаба. Если отдача от масштаба п остоянна, то эта сумма равна единице.
Дифференцируя функцию (4) по L, найдем предельный продукт труда:
MPL = aL ALαL −1KαK = aLLq .
Аналогично получим выражение для предельного продукта к а- питала:
MPK = αKKq .
Отсюда следует выражение для предельной нормы замены тру - да капиталом:
MRTSLK = MPL = aL × K .
MPK aK L
Итак, если производство описывается функцией Кобба—Дугл аса, то прирост капитала, замещающий единицу труда, пропорцион ален уже достигнутой фондовооруженности труда (отношению вел ичины капитала к затратам труда).

VIII. Предельная выручка 611
Аналогичные соотношения имеют место и для функции вида (5) . Прологарифмировав обе части равенства (5), придем к выраже нию
ln q = ln A + α1 ln x1 + α2 ln x2 +...+ αn ln xn.
Отсюда видно, что логарифм объема продукта у = lnq и логарифмы затрат ресурсов zi = lnxi связаны линейным соотношением
y = a + α1z1 + α2z2 +...+ αnzn,
где а = lnА. Это обстоятельство широко используется для оценки параметров функции Кобба—Дугласа по реальным данным: под бор параметров линейной функции представляет собой сравнительно несложную задачу. Эта задача становится особенно простой , если производственная функция имеет вид (4) и к тому же исследов атель по тем или иным соображениям исходит из постоянства отдач и от масштаба. В этом случае αL = 1 − αK; разделив обе части равенства
(4) на L, приходим к выражению
q |
−α |
α |
æ |
Kö |
αK |
|
|
= AL |
K K |
K = Aç |
÷ |
, |
|
L |
||||||
|
|
è |
L ø |
|
связывающему средний продукт труда с его фондовооруженн остью. Эта связь описывается функцией с постоянной эластичност ью, и численная оценка ее параметров по данным наблюдения може т производится подобно тому, как это было сделано в разделе 2 лекции 7 при определении эластичности спроса.
VIII. Предельная выручка
Основные соотношения
Предельная выручка используется в качестве одного из осн овных средств анализа поведения фирм в условиях различных р ы- ночных структур. Многие результаты, приведенные в 26-й и пос - ледующих лекциях, основываются на том, что фирма, стремяща яся к максимуму прибыли, выбирает такой объем производства, п ри котором выполняется равенство
MR = ÌÑ. |
(1) |
Заметим, что если TR и ТС — непрерывно дифференцируемые функции объема производства, то равенство (1) является лиш ь необходимым условием максимума прибыли. Если при некотором об ъеме
