10 Билет

Вопрос 1)Т.РОЛЛЯ: Если функцияy=f(x) непрерывна на отрезке, дифференцируема внутри этого отрезка иf(a)=f(b), то существует по крайней мере одна точкаx=c(a<c<b), такая, что.

Т.ФЕРМАХ: Теорема Ферма, - утверждение, что для любого натурального числа n > 2 уравнение (уравнение Ферма) не имеет решений в целых ненулевых числах x, y, z.

Вопрос2)Второй замечательный предел:

11 билет

Вопрос1)Метод Гаусса- классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Вопрос2)Т.ЛАГРАНДЖА:Если ф-цияy=f(x) непрерывная на отрезкеи дифференцируема внутри этого отрезка, то существует по крайней мере одна точка х=с (a<c<b), такая, что

12 билет

Вопрос 1)Однородной системой линейных уравнений называется система вида:

Однородные системы всегда совместны, т.к. всегда существует тривиальное решение.

Вопрос 2)О. Точкаx0 называется точкой минимума функцииf(x), если при любом достаточно маломh>0,выполняются условия: f(-h)>f() иf(+h)>f(), т.е можно найти такую окрестность этой точки, что для любой точкиxиз этой окрестности выполняется условие f(x) >f().

О. Точкаx0 называется точкой максимума функцииf(x), если при любом достаточно маломh>0,выполняются условия:f(-h)<f() иf(+h)<f(), т.е если можно найти такую окрестность этой точки, что для любой точкиxиз этой окрестности выполняется условие:f(x) <f().Точки максимума и минимума функции называютсяточками экстремума.

Теорема.(Необходимое условие экстремума).Если функцияy=f(x) в точкеимеет экстремум, то производнаяравна нулю.

О. Точка, в которой производная равна нулю, называется стационарной. Стационарная точка необязательно является точкой экстремума функции.

О. Точка в которой производная функции равна 0 или не существует, называется критической точкой.

Теорема(Достаточное условие экстремума).Пусть функцияf(x) непрерывна на отрезке [a,b], а точкаx0 из этого отрезка является критической. Тогда:

1) если (x) < 0 на (a;x0) и(x) > 0 на (x0;b), то точкаx0–точка минимума функцииf(x);

2) если (x) > 0 на (a;x0) и(x) < 0 на (x0;b), то точкаx0–точка максимума функцииf(x).

13 Билет

вопрос 1)Векторным произведением векторовназывается вектор, который определяется следующими условиями:

1) Его модуль равен где α - угол между векторами.

2) Вектор перпендикулярен к плоскости, определяемой перемножаемыми векторами.

Основные свойства векторного произведения:1) Векторное произведениеравно нулю, если векторыколлинеарны или какой-либо из перемножаемых векторов является нулевым. 2) При перестановке местами векторов сомножителей векторное произведение меняет знак на противоположный:

Вопрос 2) Числовая последовательность — это последовательность элементов числового пространства. Пусть множество X — это либо множество вещественных чиселR, либо множество комплексных чиселC. Тогда последовательность элементов множества X называется числовой последовательностью.

Число А€ Rназывается пределом числовой последовательности, если последовательностьявляется бесконечно малой, т. е. все её элементы, начиная с некоторого, по модулю меньше любого заранее взятого положительного числа.

14 билет

Вопрос 1)

СВОЙСТВА:

1)если > 0, то тройка- правая; если<0, то тройка- левая.

2) если 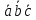=0,то векторы –комплонарны

3) а)Vпар-да=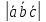; б)Vпризмы=;в)Vтетр.=

Вопрос 2)Правило Лопиталя представляет собой метод вычисления пределов, имеющих неопределенность

типа или.

Пусть aявляется некоторым конечным действительным числом или равно бесконечности.

Если и, то

Если и, то

15 билет

Вопрос 1) общ. Ур-ие прямой на плоскости: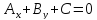

Ур-ие прямой в отрезках: =0 ; ур-ие прямой с угловым коэф.:

Вопрос 2)Функция назыв.выпуклой если её надграфик является выпуклым множеством. Функция назыв.вогнутой если её подграфик является выпуклым множеством.

Точка перегиба графика ф-ции –это точки графика в которых 2-ая производная меняет знак с «+» на «-» или с «-» на «+»