19.2 Кинетическая энергия

Кинетическая энергия является динамической мерой движения любого материального тела. Для механизма она равна сумме кинетических энергий всех его подвижных звеньев.

При вращении звена вокруг неподвижной оси (кривошипа) его кинетическая Энергия

где J о — момент инерции звена относительно оси вращения О; 1 ω₁ — угловая скорость звена (для стержня массой т1 и длиной I J0 = т1 12 /3).

Так как центр масс С1 кривошипа не совпадает с центром вращения O, то в этом случае

где JC1 — момент инерции звена ОA относительно оси, проходящей через его центр масс С1 перпендикулярно к плоскости движения; т1 — масса звена;

1 _{OC l} — расстояние от оси вращения О до центра масс С1 звена (JC1 =т112 /12). Кинетическая энергия вращающегося звена типа диска, колеса радиусом r и массой m₁, определяется также, а поскольку центр масс такого звена лежит на оси его вращения, то OC l

=0 и J0=Jc =mlr2/2.

Если звено механизма совершает плоскопараллельное движение (шатун), его кинетическая энергия

где т2 - масса шатуна; υ_C2 - скорость его центра масс С2; JС2 - момент инерции звена относительно подвижной оси, проходящей через центр масс С2;

ω2 — угловая скорость вращения шатуна при плоскопараллельном движении.

При поступательном движении звена (ползун) его кинетическая энергия

где m₃- масса ползуна; υ_C3— скорость его центра масс С3.

Для кривошипно-ползунного механизма, имеющего три подвижных звена,

кинетическая энергия

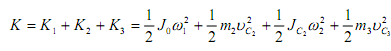
В общем случае кинетическая энергия всего механизма

19.3 Обобщенные силы механизмов

Обобщенные силы определяются из выражения элементарной работы механической системы. Работа является количественной мерой действия силы при превращении механического движения в другую форму (потенциальная энергия, теплота, электричество и т.д.). Пусть механическая система состоит из п материальных точек, имеет Wстепеней свободы, т.е. ее положение определяется Wобобщенными координатами. Для определения обобщенной силы Qi соответствующей обобщенной координате qh сообщим координате бесконечно малое приращение qδ, не изменяя остальных обобщенных координат. Тогда точки системы (механизма) получат бесконечно малые перемещения, допускаемые связями, т.е. одни из так называемых возможных перемещений системы. Возможными перемещениями называют воображаемые бесконечно малые перемещения, допускаемые наложенными на звенья связями. Поэтому криволинейные перемещения заменяют прямолинейными отрезками, отложенными по касательным к траекториям точек . Так, например, возможным перемещением кривошипа является его поворот на бесконечно малый угол δϕ₁ вокруг точки О, а точка А его конца должна при этом переместиться по дуге окружности. Возможное перемещение точки А представляем в виде прямолинейного отрезка, отложенного по касательной к траектории точки А. Элементарная работа всех сил механизма при возможном приращении одной обобщенной координаты δq _i

где F_k — силы, действующие на звенья механизма; — возможные перемещения точек приложения соответствующих сил; — угол между направлениями вектора силы F_k и вектора точки ее приложения . Отношение работы дW_i к приращению обобщенной координаты δq_i , представляет собой обобщенную силу Q_i соответствующую обобщенной координате q_i. Для определения обобщенной силы Q_w, соответствующей обобщенной координате q_w, сообщим координате бесконечно малое приращение дq_w,, не изменяя остальных обобщенных координат. Далее, ипользуя последнее выражение, определим обобщенную силу Q_w. Число обобщенных сил, как и уравнений Лагранжа второго рода, равно числу обобщенных координат механизма.