
- •Введение
- •1. Случайные события. Сумма и произведение событий
- •2. Расчеты по формуле полной вероятности и формуле Бейеса
- •3. Характеристики случайных величин
- •4. Характеристики случайных процессов
- •5. Анализ линейных преобразований случайных процессов
- •6. Анализ нелинейных преобразований случайных процессов
- •Библиографический список
f гр ,1=50 кГц , дисперсия шума на выходе второго фильтра превышает
дисперсию на выходе первого в 10 раз. Найти частоту среза второго фильтра.
5.4. На RL-фильтр нижних частот с параметрами L= 2 мГн, R= 4 кОм подается квазибелый шум с дисперсией 25 В2 и наибольшей частотой в спектре f m=5 МГц . Определить дисперсию процесса на
выходе цепи.
5.5. Случайное напряжение с корреляционной |
функцией |
K (τ)=a e−b|τ| подается на вход резистивного делителя |
напряжения |
(R1=R2=1 кОм). Найти корреляционную функцию и дисперсию процесса на выходе цепи, если a=4 В2 , b=100 1с .
6. Анализ нелинейных преобразований случайных процессов
Необходимые теоретические сведения
В настоящем разделе рассмотрение вопросов нелинейных преобразований случайных процессов ограничено случаем воздействия стационарных случайных процессов на нелинейные безынерционные цепи. Такие цепи не содержат реактивных элементов, поэтому мгновенное значение процесса η(t ) на выходе цепи в каждый момент
времени зависит только от мгновенного значения процесса ξ(t ) на
входе в этот же момент времени и не зависит от значений входного процесса в предыдущие моменты времени.
Примером нелинейной безынерционной цепи может служить нелинейное сопротивление. Если на него воздействует случайное напряжение, то отклик – протекающий через него случайный ток. Цепь в этом случае описывается вольт-амперной характеристикой i=ϕ(u) .
По заданной реализации случайного напряжения ξ(t ) и вольт-амперной характеристике i=ϕ(u) можно графическим методом определить реализацию тока η(t ) через нелинейное сопротивление
(см. рис. 6). Графическое решение задачи аналогично решению для случая детерминированного сигнала (см. [7]). Поскольку ξ(t ) –
случайная функция времени, то и процесс η(t ) тоже случаен, поэтому
отдельно взятая его реализация не обладает большой информативностью.
35
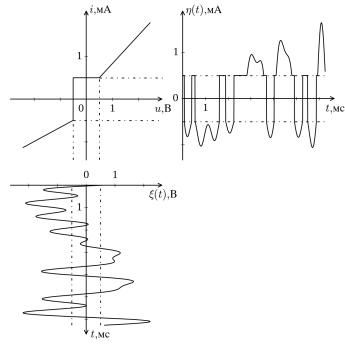
Рис. 6. Определение реализации случайного процесса на выходе нелинейного сопротивления графическим методом
Практический интерес заключается в определении неслучайных характеристик процесса на выходе нелинейной цепи.
Наиболее простым является расчет плотности вероятности f (η) по известной плотности вероятности f (ξ) процесса на входе и
проходной характеристике цепи. Поскольку закономерности нелинейных преобразований не зависят от физической природы отклика и воздействия, удобнее рассматривать проходную характеристику нелинейной безынерционной цепи (четырехполюсника) без уточнения ее физического смысла: y=ϕ(x) , где x – воздействие
(ток или напряжение), y – отклик (ток или напряжение).
Если заданы f (ξ) и проходная характеристика y=ϕ(x) , то
плотность вероятности процесса на выходе цепи определяется выражением:
36
|
|
|
|
|
|
d x |
|
f (ξ) |
|
|
||||
|
|
f (η)= f (ξ)| |
|
|x=ξ |
= |
|
|
|
x =ξ , |
(6.1) |
||||
d ϕ |
| |
d ϕ |
| |
|||||||||||
|
|
d x |
|
|
||||||||||
где | |
|
d ϕ |
|x =ξ |
– модуль производной проходной характеристики в точке |
||||||||||
|
d x |
|||||||||||||
x=ξ ; |
|
|
|
|
|
|
|
|
|
|
||||
| |
d x |
|x =ξ |
– модуль |
производной функции, обратной |
проходной |
|||||||||
d ϕ |
||||||||||||||
характеристике ( x=ϕ−1( y) ) в точке x=ξ . |
|
|
||||||||||||
Если проходная характеристика вертикальна в какой-то точке |
x0 , |
|||||||||||||
которая соответствует интервалу выходной величины [ y01 , y02 ] , |
то |
|||||||||||||
вероятность того, что процесс на выходе примет значение из этого интервала, равна нулю. На рис. 6. значению входного напряжения –0,5
В соответствует вертикальных участок |
проходной |
характеристики |
||||
[−0,5,0 ,5] |
мА. При этом на интервале |
[−0,5,0 ,5] мА процесс η(t ) |
||||
меняется |
скачком, |
т. е. |
бесконечно |
быстро. |
Вероятность |
|
P {−0,5 мА<η<0,5 мА} |
равна |
вероятности |
P {ξ=−0,5В } , которая |
|||
стремится к нулю, т. к. процесс на входе в каждый момент времени представляет собой непрерывную случайную величину.
|
|
|
|
0,5 |
|
Поскольку P {−0,5 мА<η<0,5 мА} 0 , то и |
∫ f (η)d η 0 , что |
||||
возможно только если f |
|
|
−0,5 |
|
|
(η) 0 при n [−0,5;0,5] мА. |
|
||||
Если |
проходная характеристика имеет горизонтальный участок |
||||
[x11 , x12 ] , |
которому соответствует |
значение y1 , то в |
точке η= y1 |
||
плотность |
вероятности |
процесса |
на выходе |
цепи |
обращается в |
дельта-функцию pδ(y1) площадью p=P {x11 <ξ<x12 } . Это
происходит, потому что все значения входного процесса из интервала [x11 , x12 ] отображаются проходной характеристикой в единственную
точку y1 , и вероятность P {η= y1} перестает быть бесконечно малой. Поэтому плотность вероятности устремляется к бесконечности.
На рис. 6 все значения процесса ξ(t ) из интервала [−0,5,0,5] В
отображаются проходной характеристикой в единственное значение
η=0,5 мА.
37
Вслучае, если обратная функция x=ϕ−1( y) обладает
неоднозначностью, т. е. какому-то значению y2 соответствуют k значений x1, x2, ... , xk , плотность вероятности процесса на выходе в точке η= y2 определяется как сумма:
f (η)= |
f (ξ) |
f (ξ) |
+...+ |
f (ξ) |
|||||||
|
|
|
ξ=x 1,+ |
|
|
|
ξ=x2, |
|
ξ=x k , . |
||
| |
d ϕ |
| |
| |
d ϕ |
| |
|dd ϕx| |
|||||
|
d x |
d x |
|||||||||
|
|
|
|
x=ξ |
|
|
|
x=ξ |
|
|
x=ξ |
Для определения корреляционной функции процесса на выходе нелинейной цепи необходимо знать двумерную плотность вероятности процесса на входе:
∞ ∞
K η(τ)=∫ ∫[ϕ(ξ1)−ϕ(mξ)][ϕ(ξ2)−ϕ(mξ)] f (ξ1 ,ξ2 ,t1 ,t1+ τ) d ξ1 d ξ2 .
−∞ −∞
Спектральную плотность мощности процесса η(t ) можно найти из корреляционной функции по теореме Винера-Хинчина.
Вопросы анализа нелинейных преобразований случайных процессов подробно рассмотрены в [3–5].
Пример 6.1 |
|
|
|
|
|
|
||
Процесс ξ(t ) |
распределен по нормальному закону: |
|||||||
|
|
1 |
|
e− |
ξ2 |
|||
f (ξ)= |
|
|
2 σξ2 |
. |
||||
|
|
|
|
|||||
σξ |
√2 |
π |
||||||
|
|
|
|
|||||
Найти плотность вероятности процесса η(t ) на выходе нелинейной цепи, проходная характеристика которой:
|
|
y( x)= |
a1 x+b1, x x1 , |
|
|
|
|
|
|
|
|
|
|
|
(6.2) |
|||
|
|
b2, |
x1< x x2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
{a3 x+b3, x> x2 . |
|
|
|
1 |
|
|
|
1 |
|
|
|
1 мА |
||||
|
|
Значения параметров |
σ |
=1 В , |
a = |
В−1 |
, |
b =− |
мА , |
b |
= |
|||||||
|
|
=2 В−1 , |
b = 1 мА , x |
ξ |
|
1 |
|
3 |
|
|
1 |
3 |
|
2 |
|
2 |
||
, |
a |
=−0,5В , |
x |
=0,5 В |
|
соответствуют рис. 6. |
||||||||||||
|
3 |
3 |
3 |
6 |
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
Решение
38
Найдем производную проходной характеристики: |
|
|
|
||||||||||||||||||||||||||||||
dy |
|
|
a1, x x1 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= 0, x1 <x x2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
dx |
|
|
{a3, |
x>x2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Воспользуемся |
|
выражением |
(6.1), |
|
|
заменяя |
|
|
в |
неравенствах, |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{ |
|
f (ξ) |
, ξ x1, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (ξ) |
|
|
|
|
|
|
|a1| |
|
||||||||||
задающих интервалы, x на ξ: f (η)= |
|
= |
|
f (ξ) |
, |
x1 <ξ x2 ,= |
|||||||||||||||||||||||||||
|
d ϕ |
|
|||||||||||||||||||||||||||||||
|
|
|0| |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|x=ξ |
|
|
f (ξ) |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d x |
|
|
, |
ξ>x2 ; |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|a3| |
|
||||||||
|
|
1 |
|
|
|
|
|
e− |
|
ξ2 |
|
|
1 |
|
|
|
|
e− |
|
ξ2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
2σξ2 , ξ x1 , |
|
|
|
|
|
|
2 σξ2 |
|
, ξ x1 , |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|a1|σξ √2π |
|a1|σξ √2 π |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.3) |
||||||||||||||||
= p δ(η−ϕ(ξ)), x1<ξ x2 ,= p δ(η−b2) , |
|
|
x1<ξ x2 , |
||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
− |
ξ2 |
1 |
|
|
|
|
− |
ξ2 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
2 σ2 |
|
|
|
|
|
2 σ2 |
|
|
|
|
|
||||||||||||||||
{ |
|
|
|
e |
|
ξ , ξ>x2 ; |
{ |
|
|
|
e |
|
|
ξ |
, ξ>x2. |
||||||||||||||||||
|a3|σξ √ |
|
|
|a3|σξ √ |
|
|
||||||||||||||||||||||||||||
2 π |
2π |
|
|
|
|
||||||||||||||||||||||||||||
На втором интервале плотность вероятности |
f |
(η) |
представляет |
||||||||||||||||||||||||||||||
собой δ-функцию, площадь которой p=P {x1 <ξ x2} . |
|
|
|||||||||||||||||||||||||||||||
Для получения окончательного вида функции |
|
|
f (η) |
требуется в |
|||||||||||||||||||||||||||||
первом и третьем уравнениях системы (6.3) выразить ξ через η. Для этого следует в соответствующих уравнениях системы (6.2) заменить x на ξ, y на η:
|
|
|
|
η−b1 |
, |
η−b1 |
|
x1 , |
|
a1 ξ+b1, |
ξ x1 , |
|
{ |
a1 |
a1 |
|
|||
η={a3 ξ+b3, |
ξ> x2 ; |
ξ= |
η−b3 |
|
, |
η−b3 |
|
> x2 . |
|
|
|
|
a3 |
|
a3 |
|
|||
В неравенствах, задающих интервалы, значения ξ выражены через η. Упрощая эти неравенства, получим:
39

|
|
η−b1 |
, |
η x1 a1 +b1 , |
||
|
|
|
a1 |
|||
ξ= |
|
|
|
|
(6.4) |
|
|
η−b3 |
|
|
|||
|
{ |
|
|
, |
η>x2 a3+b3 . |
|
|
a3 |
|
||||
Подставляя первое и второе уравнение (6.4) вместо ξ соответственно в первое и второе уравнение (6.3), получим выражение
|
1 |
|
|
|
|
e− |
(η−b1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
2σξ2 a12 , η x |
1 |
a +b |
1 |
, |
|||
|
|
|
|
|
|||||||||
|a1|σξ√2 |
π |
|
|
|
|
|
1 |
|
|||||
|
|
|
|
|
|
|
|
|
|||||
для f (η) , зависящее от η: f (η)= pδ(η−b2 ), x1 a1 +b1<η x2 a3 +b3 |
, (6.5) |
||||||||||||
|
|
|
|
|
|
|
|
(η−b )2 |
|
|
|
|
|
1 |
|
|
|
|
− |
3 |
|
|
|
|
|
||
|
|
|
|
2σ ξ2 a32 |
|
|
|
|
|
||||
{ |
|a3|σξ √ |
|
|
e |
|
|
, η> x2 a3 +b3 . |
||||||
2π |
|
|
|||||||||||
Второе неравенство ( x1 a1+b1 <η x2 a3+b3 ) получено из анализа
графика проходной характеристики на рис. 6. Поскольку горизонтальный участок проходной характеристики расположен на верхней границе вертикального участка, то δ-функция, соответствующая горизонтальному участку, будет находиться на правой границе интервала, где плотность вероятности f (η) 0 ,
соответствующего вертикальному участку проходной характеристики. Таким образом, на интервале x1 a1+b1 <η x2 a3+b3 плотность
вероятности f (η)=0+ pδ(η−b2) .
Заметим, что на интервале η x1 a1+b1 функция f (η) совпадает с нормальным распределением, имеющим параметры m=b1 , σ=σξ a1 , а на интервале η> x2 a3+b3 – с нормальным распределением, имеющим параметры m=b3 , σ=σξ a3 . Вид распределения на этих интервалах не изменился, т. к. проходная характеристика на них линейна.
Найдем вероятность р (множитель при δ-функции) при помощи таблицы функции Лапласа:
p=Φ(σx2ξ )−Φ(σx1ξ )=Φ(0,5)−Φ(−0,5)=0,6915−0,3085=0,383 . Подставляя числовые значения в (6.5), получим окончательный
40

|
3 |
|
|
− |
9 |
(η+ |
1 |
)2 |
1 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
2 |
3 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
, |
|
η −0,5 мА , |
|
||||||
|
|
|
|
|
|
|
|
|
|
мА |
|
|||||||||||||
|
√2 |
π |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ответ: f (η)= 0,383δ(η−0,5) |
|
1 |
|
|
, −0,5 мА<η 0,5 мА , |
(6.6) |
||||||||||||||||||
мА |
||||||||||||||||||||||||
{ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
)2 |
|
|
|
|||||
|
|
|
|
3 |
|
|
− |
9 |
(η− |
1 |
1 |
|
|
|||||||||||
|
|
|
|
|
|
8 |
6 |
|
||||||||||||||||
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
, η>0,5 мА. |
|
|||||||
|
|
|
|
2√ |
|
|
|
|
|
|
|
|
|
мА |
|
|||||||||
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|||||||||||
Графики на рис. 7 поясняют преобразования плотности |
||||||||||||||||||||||||
вероятности процесса |
ξ(t ) |
|
при его прохождении через нелинейную |
|||||||||||||||||||||
цепь. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 7. Графическое представление преобразования плотности вероятности процесса ξ(t ) при прохождении его через нелинейную цепь
Ответ: f (η) имеет вид (6.6)
41
Задачи
6.1. Случайное напряжение с равномерным распределением в пределах [ξ1 , ξ2] В проходит подается на вход нелинейной цепи
y=x3 . Найти плотность вероятности процесса на выходе цепи, если
ξ1=−2 В , ξ2=2 В . Размерность отклика цепи – мА.
6.2.Случайный процесс с равномерным распределением в пределах [ξ1 , ξ2] подается на вход нелинейного элемента с проходной
0,5 x мВ , x<0 , |
|
|
|
характеристикой y={2 x мВ , |
x 0. |
. Найти плотность |
вероятности |
процесса на выходе цепи, если |
ξ1=1 В , ξ2=3В . |
|
|
6.3. Датчик случайных чисел выдает равномерно распределенные |
|||
числа в интервале [0,1] . Для моделирования отказов |
электронной |
||
аппаратуры требуется преобразовать равномерно распределенные числа от датчика в числа с показательным распределением:
0, x<0 , |
|
|
|
f (η)={λ e−λη , |
x 0. |
Определить вид |
|
нелинейного |
элемента, |
способного |
|
преобразование. |
|
|
|
проходной характеристики
осуществить нужное
6.4. Датчик случайных чисел выдает равномерно распределенные числа в интервале [0,1] . Для численного эксперимента необходимы числа с равномерным распределением на интервале [−15 ,15] . Определить проходную характеристику элемента, осуществляющего заданное преобразование.
6.5. Случайный процесс с нормальным распределением подается на нелинейный элемент с проходной характеристикой y=|x| . Найти математическое ожидание процесса на выходе цепи, если параметры распределения процесса на входе: m=0 , σ=3 мВ .
6.6. Процесс с равномерным распределением в пределах примерно от –4 до +4 В подается на односторонний ограничитель с
0, |
x<0, |
единичным наклоном проходной характеристики: y={x , |
x 0. |
Нарисовать плотность вероятности на выходе. |
|
6.7. Процесс с равномерным распределением в пределах примерно от –4 до +4 В подается на идеальный двусторонний
42
