
Лабораторная работа 1
.pdfЛабораторная работа№1. Метод множителей Лагранжа
(методы классическоговариационногоисчисления)
Цель работы: изучение свойств оптимальной системы, синтезированной методом множителей Лагранжа.
1.1. Теоретические сведения
Правило множителей Лагранжа для задач оптимального управления с закрепленными концами и фиксированным временем. Если концы закреплены и время фиксировано, то задачу оптимального управления классического типа можно сформулировать как следующую задачу Лагранжа классического вариационного исчисления:
|
|
|
|
|
|
i = 1, 2, …, n; |
(1.1а) |
|
|
xi = fi (x,u,t), |
|||||
|
ϕk (x,u,t) = 0 , |
k = 1, 2, …, l; |
(1.1б) |
||||
x (t |
0 |
) = x0 , |
x (t |
f |
) = x f , i = 1, 2, …, n; |
(1.1в) |
|
i |
i |
i |
|
i |
|
||
|
|
|
t f |
|
|
|
|
|
|
J = ∫ f0 (x,u,t)dt → min . |
(1.1г) |
||||
|
|
|
t0 |
|
|
|
|
Предполагается, что |
функции |
|
fi (x,u,t) (i = 0,1, …, n) и |
ϕk (x,u,t) |
|||
(k = 1, 2, …, l) являются непрерывными и дифференцируемыми по всем своим аргументам, управление u(t) принадлежит классу кусочно-непрерывных функций, а траектории x(t) — классу кусочно-гладких функций.
Функция u(t) называется кусочно-непрерывной на интервале [t0, tf], если она (т.е. каждая его координата) непрерывна всюду на интервале [t0, tf], за исключением конечного числа точек, где она имеет разрыв первого рода (существуют конечные пределы слева и справа). Функция x(t) называется кусочно-гладкой на интервале [t0, tf] если на [t0, tf] она сама непрерывна, а ее производная кусочно-непрерывна.
1
Управление u(t) из класса кусочно-непрерывных функций называют допустимым управлением, а траекторию x(t) из класса кусочно-гладких
функций ‒ допустимой траекторией. Пару (u(t), x(t)) называют допустимой,
если допустимыми являются u(t) и x(t). В каждой конкретной задаче на допустимые управления и траектории могут быть наложены дополнительные ограничения. Поэтому при рассмотрении определенного класса задач эти понятия могут уточняться.
Функция
H = ∑n ψi fi +∑l λkϕk |
|
|||
|
i=0 |
|
k =1 |
|
называется функцией Гамильтона или гамильтонианом, ψi |
(i = 0,1,2, …, n) и |
|||
λk (k=1,2, …, n) – множители Лагранжа. |
|
|
||
Уравнения |
|
|
|
|
|
∂H |
, |
i = 1, 2, …, n; |
(1.2а) |
ψi = − |
∂xi |
|||
|
|
|
|
|
∂H = 0, |
|
s = 1, 2, …, τ. |
(1.2б) |
|
∂us |
|
|
|
|
называются уравнением Эйлера-Лагранжа. Уравнения (1.2а) представляют собой условие экстремума гамильтониана при каждом фиксированном t [t0 ,t j ], и их называют условием стационарности.
Правило множителей Лагранжа закрепленными концами и фиксированным временем. Если допустимая пара (u(t), x(t)) является решением задачи оптимального управления (1.1), то найдутся такие не равные одновременно нулю множители Лагранжа, что эта пара удовлетворяет уравнениям Эйлера-Лагранжа (1.2).
В соответствии с этим правилом, чтобы найти оптимальное управление и оптимальную траекторию, надо решить совместно уравнения (1.1а), (1.1б), и (1.2) при краевых условиях (1.1в).
Если оптимальное управление u(t) имеет разрыв первого рода в какихлибо точках, то оно само и соответствующая ему траектория x(t) должны
2
удовлетворять указанным выше уравнениям лишь в точках непрерывности управления. В точках разрыва управления, которые называются угловыми, должны выполняться условия
ψ − =ψ +, |
H − = H +, |
где индексы « – » и «+» обозначают левый и правый пределы соответствующих функций.
Эти условия называются условиями Вейерштрасса-Эрдмана.
Множители Лагранжа определяются с точностью до постоянного множителя. Действительно, они входят в уравнения Эйлера-Лагранжа линейно и однородно, и эти уравнения не изменятся, если все множители умножить на одно и то же постоянное число. Поэтому в случае, когда ψ0 ≠ 0, (этот случай называют неособым), не нарушая общности, будем принимать ψ0 = −1.Дальше, если особо не оговаривается, будет подразумеваться, что имеет место неособый случай.
Как отмечалось, уравнения Эйлер-Лагранжа является необходимым условием, т.е. любое решение задачи оптимального управления (1.1) является экстремалью, т.е. удовлетворяет уравнениям Эйлера-Лагранжа, но не любая экстремаль, удовлетворяющая граничным условиям, является решением задачи (1.1). Но если решение задачи существует и экстремаль, удовлетворяющая граничным условиям, единственна, то, очевидно, эта экстремаль и будет решением.
Пример 1.1. Определить оптимальное программное управление для поворота вала двигателя на угол 1 радиан с последующей остановкой за 10 сек при минимальном расходе энергии без учета момента сопротивления (uс = 0):
x1 = x2 , x2 =u ; x1(0) = x2 (0) = 0,
10
x1(10) =1, x2 (10) = 0; J = ∫u2dt → min.
0
Так как задача имеет физический смысл, т.е. имеет место неособый случай, то полагаем ψ0 = −1. Составим гамильтониан:
3
H = −u2 +ψ1x2 +ψ2u.
Уравнения Эйлера-Лагранжа принимают вид
|
= − |
∂H |
= 0, |
|
= − |
∂H |
= −ψ1, |
∂H |
= −2u +ψ2 = 0. |
|
ψ1 |
∂x |
ψ2 |
∂x |
2 |
∂u |
|||||
|
|
1 |
|
|
|
|
|
|
|
|
Эта система имеет решение
ψ |
1 |
=C , |
ψ |
2 |
= −C t +C |
, u = |
−C1t +C2 |
. |
|
|
|||||||||
|
1 |
|
1 |
2 |
2 |
|
|||
|
|
|
|
|
|
|
|
||
Подставив полученное выражение для управления в уравнения объекта и решив их, получим
x |
|
= − |
C t2 |
+ |
C |
t |
+C |
, |
x = − |
C t3 |
+ |
C |
t2 |
+C |
t +C |
. |
2 |
1 |
2 |
|
1 |
2 |
|
||||||||||
|
|
4 |
|
2 |
|
3 |
|
1 |
12 |
|
4 |
3 |
4 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Из краевых условий имеем:
x2 (0) =C3 = 0, x1(0) =C4 = 0, x2 (10) = −25C1 +5C2 = 0, x1(10) = −2503 C1 +25C2 =1.
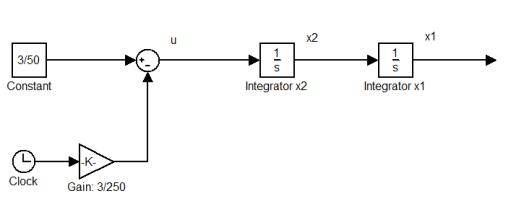
Отсюда находим С1 = 3/125, C2 = 3/25, C3 = 0, C4 = 0. Оптимальное программное управление и оптимальные траектории имеют вид
u *(t) = |
1 |
|
|
3 |
t + |
3 |
|
|
* |
|
1 |
|
|
1 |
|
3 |
|
2 |
|
|
* |
|
3 |
|
|
1 |
|
2 |
|
|
|||
|
|
− |
|
|
|
, |
x |
|
(t) = |
|
|
|
− |
|
t |
|
+3t |
|
, |
x |
|
(t) = |
|
|
− |
|
|
t |
|
+t . |
|||
2 |
125 |
25 |
|
100 |
5 |
|
|
|
50 |
10 |
|
||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||
Структурная |
|
схема |
оптимальной |
|
системы |
|
реального |
времени |
с |
||||||||||||||||||||||||
оптимальным программным управлением будет иметь вид:
Правило множителей Лагранжа для задач оптимального управления с подвижными концами. Задача оптимального управления классического типа
4
с подвижными концами и фиксированным временем формулируется
следующим образом: |
i = 1, 2, …, n; |
(1.3а) |
xi = fi (x,u,t), |
||
|
|
|
ϕk (x,u,t) = 0 , |
k = 1, 2, …, l; |
(1.3б) |
g j [x(t0 ), x(t f ),t0 ,t f ] = 0, j = 1, …, q < 2n; |
(1.3в) |
|
|
t f |
|
J = g0[x(t0 ), x(t f ),t0 ,t f ]+ ∫ f0 (x,u,t)dt → min . |
(1.3г) |
|
|
t0 |
|
Граничные условия (1.3в) предполагаются независимыми, |
функции |
|
g j [x(t0 ), x(t f ),t0 ,t f ] (j = 1, 2, …, q) – непрерывными и дифференцируемыми по всем своим аргументам. На остальные функции накладываются такие же требования, как и в случае задачи с закрепленными концами.
Эта задача отличается от рассмотренной выше задачи тем, что изменяются краевые условия и критерий оптимальности может иметь любой из указанных при классификации видов, т.е. в этом случае задача оптимального управления может быть вариационной задачей Лагранжа, Больца и Майера. Когда концы закреплены и время фиксировано, задача оптимального управления может быть только задачей Лагранжа.
Дифференциальные уравнения объекта и уравнения Эйлера-Лагранжа имеют порядок n. Поэтому при их решении будем иметь 2n постоянных интегрирования. При закрепленных концах граничные условия представляют собой 2n соотношений, которые позволяют определить все постоянные интегрирования. Однако при подвижных концах траектории граничных условий не достаточно, чтобы можно было их определить. Недостающие соотношения доставляют условия трансверсальности, которые имеют следующий вид:
ψi (t0 ) = − |
∂G |
, |
ψi (t f ) = − |
|
∂G |
, i =1,2,..., n, |
|||
∂xi (t0 ) |
|
∂xi (t f ) |
|||||||
|
|
|
|
|
|
||||
|
H |
|
= |
∂G , H |
|
|
= − |
∂G . |
|
|
|
|
|
||||||
|
|
|
t=t0 |
|
∂t0 |
|
t=t f |
∂t f |
|
|
|
|
|
|
|||||
(1.4a)
(1.4б)
5
Здесь
G= ∑q vi gi ,
i=0
где vi (i = 0,1,.., q) – постоянные неопределенные множители, при этом v0 =ψ0 (ψ0 – множитель Лагранжа, который входит в гамильтониан). Функция G
называется терминантом.
Отдельные координаты граничных точек могут быть фиксированы. Соотношения, определяющие эти координаты, в выражение для терминанта G не включаются, и так как при определении необходимых условий они не варьируются, в условия трансверсальности не нужно включать соотношения, содержащие частные производные по этим координатам. В частности, если начальная точка закреплена, т.е. заданы все координаты точки x(t0), то в условии (1.4а) все первые соотношения с частными производными по xi(t0) должны быть исключены; если время фиксировано, то отпадают условия (1.4б).
Правило множителей Лагранжа с подвижными концами. Если допустимая пара (u(t), x(t)) является решением задачи оптимального управления (1.3), то найдутся такие не равные одновременно нулю множители Лагранжа, что эта пара удовлетворяет уравнениям Эйлера-Лагранжа (1.2) и условиям трансверсальности (1.4).
Если управление терпит разрыв, то решение (u(t), x(t)) должно удовлетворять уравнениям Эйлера-Лагранжа в точках непрерывности управления. В угловых точках (в точках разрыва управления) должны выполнятся условия Вейерштрасса-Эрдмана.
Чтобы получить решение задачи (1.3), нужно решить уравнения (1.3а), (1.3б) совместно с уравнениями Эйлера-Лагранжа (1.2) при краевых условиях (1.3в) и условиях трансверсальности (1.4).
Пример 1.2. Определить оптимальное программное управление для поворота вала двигателя на угол 1 радиан без последующей остановки за 10 сек при минимальном расходе энергии без учета момента сопротивления (uс = 0):
x1 = x2 , x2 =u ; x1(0) = x2 (0) = 0,
6
10
x1(10) =1, J = ∫u2dt → min.
0
Составим гамильтониан и уравнения Эйлера-Лагранжа принимают:
H = −u2 +ψ1x2 +ψ2u.
|
= − |
∂H |
|
0, |
|
|
|
|
∂H |
|
|
|
∂H |
= −2u +ψ2 = 0. |
|||||||||||
ψ1 |
|
∂x = |
ψ |
2 = −∂x |
= −ψ1, |
∂u |
|||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
Эта система имеет решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
ψ |
1 |
=C , |
ψ |
2 |
|
= −C t +C |
, |
|
u = |
−C1t +C2 |
. |
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В данном случае G = 0, |
и нефиксированной является только координата x2 (10) . |
||||||||||||||||||||||||
Поэтому условие трансверсальности принимают вид |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
ψ2 |
(10) = |
|
∂G |
|
= 0. |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
∂x2 (10) |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Исходя из этого условия находим ψ2 (10) = −C110 +C2 =0, |
или C2 =10C1 . |
||||||||||||||||||||||||
Соответственно для |
|
управления |
|
получаем |
|
u =C1(10 −t) / 2. Подставив это |
|||||||||||||||||||
выражение в уравнение объекта и проинтегрировав, получим |
|
|
|
|
|||||||||||||||||||||
x |
|
= |
C |
|
|
|
|
|
|
|
, |
x = |
C |
(10t2 − |
t3 |
) +C t +C |
. |
||||||||
2 |
|
1 (20t −t2 ) +C |
|
1 |
|
||||||||||||||||||||
|
|
|
4 |
|
|
|
|
|
|
3 |
|
|
1 |
|
4 |
|
|
|
3 |
|
3 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Учитывая краевые условия |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x (0) =C |
4 |
= 0, |
x |
(0) =C = 0, |
x (10) = |
500 C =1, |
|
|||||||||||||||||
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
1 |
|
|
3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
находим оптимальное программное управление и оптимальные траектории |
|||||||||||||||||||||||||
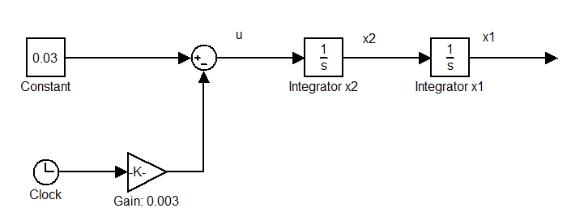
u *(t) =0,003(10 −t), x* (t) = 0,0005(30t2 −t3 ), x* (t) = 0,0015(20t −t2 ) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
и строим структурную схему оптимальной системы реального времени:
7
1.2. Порядок выполнения работы
2.1.Определить оптимальное программное управление и оптимальные траектории движения системы в соответствии с вариантом задания.
2.2.Собрать схему оптимальной системы программного управления.
2.3.Построить графики переходных процессов по переменным состояния и управляющему воздействию и фазовый портрет системы.
2.4.По графику x1(t) определить время переходного процесса.
1.3. Содержание отчета
3.1.Цель работы.
3.2.Исходные данные для выполнения работы, модель системы, структурная схема.
3.3.Расчет оптимального программного управления и оптимальных программных траекторий движения системы.
3.4.Фазовый портрет и временные характеристики.
3.5.Выводы по работе.
8
1.4. Варианты заданий
№ |
Мат. модель |
Граничные условия |
Функционал |
варианта |
|
|
|
1 |
x1 |
= x2 , |
x2 |
=u |
|
x1 |
(0) = x2 (0)= 0, |
10 |
||||
|
|
|
|
|
|
|
|
x1 |
(10) =10, |
x2 (10) = 0 |
J = ∫u2dt → min |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2 |
x1 |
= x2 , |
x2 |
=u |
|
x1 |
(0) = x2 (0)= 0, x1(10) =10 |
10 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
J = ∫u2dt → min |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
3 |
x1 |
= x2 , |
x2 |
=u |
|
x1 |
(0) = x2 (0)= 0, |
10 |
||||
|
|
|
|
|
|
|
|
x2 |
(10) =10 |
|
J = ∫u2dt → min |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
4 |
x1 |
= x2 , |
x2 |
=u −1 |
x1 |
(0) = x2 (0)= 0, |
10 |
|||||
|
|
|
|
|
|
|
|
x1 |
(10) =10, |
x2 (10) = 0 |
J = ∫u2dt → min |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
5 |
x1 |
= x2 , |
x2 |
=u −1 |
x1 |
(0) = x2 (0)= 0, x1(10) =10 |
10 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
J = ∫u2dt → min |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
6 |
|
= x2 , |
|
= |
|
− |
|
x(0) = 0, x |
(10) =10; |
10 |
||
x1 |
x2 |
|
u |
|
1 |
|
2 |
|
|
J = ∫u2dt → min. |
||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
7 |
x1 |
= x2 , |
x2 |
=u |
|
|
x1 |
(0) =5 , |
x2 |
(0) = 0 , |
10 |
|
|
|
|
|
|
|
|
|
x1 |
(10) =10, |
x2 (10) = 0 |
J = ∫u2dt → min |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
8 |
x1 |
= x2 , |
x2 |
=u |
|
x1 |
(0) = 0, |
x2 |
(0) =5, |
10 |
||
|
|
|
|
|
|
|
|
x1 |
(10) =10, |
x2 (10) = 0 |
J = ∫u2dt → min |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
9 |
x1 |
= x2 , |
x2 |
=u −1 |
x1 |
(0) =5 , |
x2 |
(0) = 0 , |
10 |
|||
|
|
|
|
|
|
|
|
x1 |
(10) =10, |
x2 (10) = 0 |
J = ∫u2dt → min |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
10 |
x1 |
= x2 , |
x2 |
=u −1 |
x1 |
(0) = 0, |
x2 |
(0) =5, |
10 |
|||
|
|
|
|
|
|
|
|
x1 |
(10) =10, |
x2 (10) = 0 |
J = ∫u2dt → min |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
9
