Лабораторная работа № 3.

Метод фазовой плоскости синтеза оптимальной по быстродействию системы

Цель работы: изучение свойств оптимальной по быстродействию системы, синтезированной на основе синтеза фазовой плоскости.

3.1. Теоретические сведения

Пусть задана вполне управляемая линейная стационарная система

все корни характеристического уравнения которого действительны. Заметим, что ограничения более общего вида α ≤u ≤ β , где α <0 и β >0 , введением нового переменного v = 2u −(α + β) /(α − β) всегда приводится к приведенному выше виду u ≤1. Рассмотрим задачу синтеза оптимального по быстродействию

регулятора, обеспечивающего перевод системы из произвольной начальной точки в начало координат.

Так как управление скалярное, условие нормальности совпадает с условием управляемости, поэтому выполняются все условия теоремы об n интервалах. В соответствии с этой теоремой оптимальное управление, имея не более n интервалов постоянства, принимает только крайние значения: –1 или 1. Если представить его как функцию фазовых координат u* = u*(х), то ясно, что все фазовое пространство разбивается на два подпространства: подпространство, в котором u* = –1, и подпространство, в котором u* = 1. Гиперповерхность (при n = 2 – кривая, при n = 3 – поверхность), которая делит фазовое пространство на указанные подпространства, называют гиперповерхностью (кривой, поверхностью) переключения. Если записать уравнение гиперповерхности δ(x) =0, то, как известно, δ(x) >0 по одну

сторону от гиперповерхности и δ(x) <0 по другую. Всегда (при необходимости умножением на –1) можно выбрать функцию δ(x) так, чтобы она была

1

отрицательна в подпространстве, где u* = –1, и положительна в подпространстве, где u* = 1. Тогда, очевидно, оптимальным управлением будет u* =signδ(x). Поэтому нахождение оптимального управления с обратной

связью сводится к определению функции δ(x) , которая называется функцией переключения.

При n = 2 для нахождения функции переключения можно воспользоваться методом фазовой плоскости. На фазовой плоскости строятся семейства фазовых траекторий, соответствующих управлениям u* = –1 и u* = 1. Оптимальная траектория представляет собой часть траектории или соединение частей двух траекторий из построенных семейств. В силу граничного условия на правом конце траектории x(t f ) =0 она должна оканчиваться в начале координат.

Используя эти свойства оптимальных траекторий, нетрудно определить кривую переключения. Проиллюстрируем изложенное на простейшем примере.

Пример 3.1. Определить оптимальный по быстродействию закон управления двигателем, описываемым уравнениями

Решение. Характеристическое уравнение имеет кратный нулевой корень. Выполняются все условия теоремы об n интервалах. Оптимальное управление может принимать значения –1 или 1. Найдем соответствующие им фазовые траектории. Разделив второе уравнение на первое, получим

Проинтегрировав последнее уравнение при u = –1 и u = 1, соответственно находим

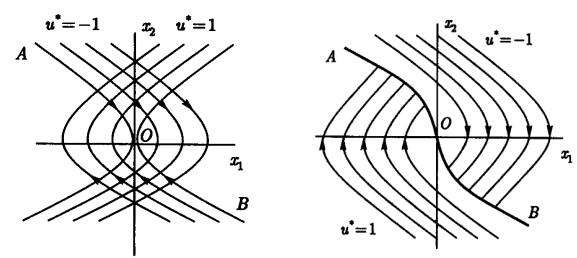
На рис. 3.1, а представлены оба семейства траекторий. Оптимальная траектория должна состоять из участка траектории одного семейства, проходящей через начальную точку, и участка траектории другого семейства,

2

проходящей через начало координат. Из сказанного следует, что переключение должно происходить на полутраекториях АО и ОВ (рис. 3.1, а). Если вначале изображающая точка движется по траектории, соответствующей u* = –1, то переключение должно произойти на полутраектории ВО, которая описывается уравнением

x22 − 2x1 =0 .

И если вначале изображающая точка движется по траектории, соответствующей u* = 1, то переключение должно произойти на полутраектории ОА, которая описывается уравнением

x22 + 2x1 =0 .

Фазовый портрет оптимальной системы представлен на рис. 3.1,б. Уравнение линии переключения АОВ, основываясь на уравнениях полутраекторий АО и OB, можно записать так:

δ(x) = −(x22 + 2x1sign x2 )sign x2 =0.

Функция δ(x) отрицательна справа от линии переключения, где u* = –1, и положительна слева, где u* = 1. Поэтому имеем

u* =sign δ(x) =sign[(x22 + 2x1 sign x2 )sign x2 ].

Заметим, что кривая АОВ может быть описана уравнением

δ~(x) = −(x22 + 2x1 sign x2 ) =0 .

Однако знак функции δ~(x) слева и справа от кривой АОВ меняемся при

переходе с верхней полуплоскости в нижнюю полуплоскость. Поэтому эта функция не может быть функцией переключения.

3

Рис. 3.1. Фазовые траектории.

Как следует из фазового портрета, переходный процесс оптимальной системы является апериодическим. Однако из-за неидеальности переключающего устройства, неточности математической модели объекта и других возмущений реальный переходный процесс может оказаться колебательным.

3.2.Порядок выполнения работы

3.2.1Определить оптимальное управление с обратной связью u* (х) в задаче максимального быстродействия при условиях, что в начальный момент х(0) = х0 (х0 – произвольный вектор), в конечный момент x(tf) = 0. В ходе решения задачи определить количество интервалов постоянства.

3.2.2Собрать схему оптимальной по быстродействию системы

управления.

3.2.3Построить графики переходных процессов по переменным состояния и управляющему воздействию и фазовый портрет системы.

3.2.4По графику x1(t) определить время переходного процесса.

4