ОиАС-6

Отсюда следует алгебраическое уравнение для определения неизвестного коэффициента p в (4.1.7):

21

уравнения (4.1.19) выбираем первое исходя из условия положительности функции v, обеспечивающего асимптотическую устойчивость синтезируемой системы, а следовательно, и выполнение краевого условия v[х( )]=0.

На основе (4.1.5) получаем

22

Матричное уравнение (4.1.12) имеет два названия:

•первое – матричное алгебраическое уравнение Риккати (смысл такого названия станет ясен несколько позже),

•второе – уравнение Лурье (А. И. Лурье получил уравнение вида (4.1.12) при исследовании абсолютной устойчивости систем регулирования).

Таким образом, процедура аналитического конструирования оптимальных регуляторов (процедура АКОР) состоит из трех операций:

1)решение системы нелинейных алгебраических уравнений;

2)выделение из всего множества этих решений матрицы P0>0 (численный метод нахождения P0 приведен ниже);

3)вычисление искомой матрицы коэффициентов усиления регулятора по формуле

Убедимся непосредственно, что матрица C, определяемая соотношением (4.1.14), обеспечивает асимптотическую устойчивость системы (4.1.1), (4.1.2).

23

Для исследования устойчивости системы

x A BC x

воспользуемся прямым методом Ляпунова. Примем в качестве функции Ляпунова

v= x'P0x > 0

ивычислим полную производную этой функции:

dvdt x P0 x x P0 x x A BC P0 x x P0 A BC xx P0 A A P0 P0BC CB P0 x

Учитывая, что матрица C определяется выражением (4.1.14), получим, с учетом того, что P0 удовлетворяет (4.1.12),

dvdt x P0 A A P0 P0BB P0 P0BB P0 xx Qx x P0BB P0 x x Qx u u 0

24

Если объект (4.1.1) полностью управляем и Q>0, то среди решений системы (4.1.12) всегда найдется и при том единственная положительно-определенная матрица P0. Напомним, что условием полной управляемости объекта (4.1.1)

является равенство

которое будем называть условием управляемости пары (A, В).

Если матрица Q – неотрицательно-определенная матрица (Q ≥ 0), то ее всегда можно представить в виде

Q = H'H,

H – матрица размеров χ n (χ – ранг матрицы Q). Среди решений (4.1.12) попрежнему существует единственная матрица Р0, если Q в функционале (4.1.3) неотрицательно-определенная матрица, удовлетворяющая условию полной управляемости пары (A', H'):

rank [H', А'Н',..., A(n–1)'H'] = n.

Требование полной управляемости пар (A, В), (А', Н') для существования и единственности Р0>0 можно ослабить, заменив его условием стабилизируемости этих пар.

25

Пример 4.1.1. Уравнение процедуры аналитического конструирования регулятора гирорамы.

Осуществим первый этап (составление уравнений (4.1.12), (4.1.13)) аналитического конструирования регулятора гирорамы.

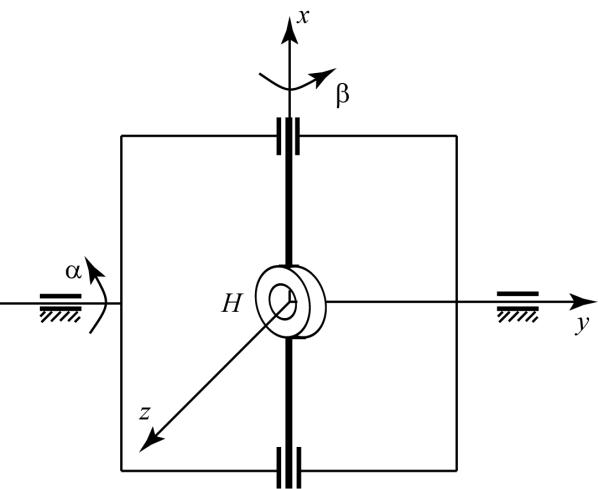
Рассмотрим трехстепенной гироскоп в кардановом подвесе.

26

Его уравнения имеют вид:

α – угол поворота наружной рамы относительно оси OY;

β – угол поворота внутреннего кольца карданова подвеса относительно оси ОХ (угол прецессии);

Jн – момент инерции наружной рамы (кольца) относительно оси OY; Jэ – экваториальный момент инерции гироскопа;

Jв, Jвх, Jвy – моменты инерции внутреннего кольца карданова подвеса относительно осей OZ, OX, OY соответственно, при этом Jвх = Jвy = Jвэ;

Н – кинетический момент гироскопа; Мх и Му – моменты относительно осей ОХ и ОУ соответственно; nα, nβ – коэффициенты демпфирования.

27

Гироскоп в кардановом подвесе используется (если установить на оси OY датчик угла) для измерения углов поворота движущегося объекта (например, ракеты) относительно оси OY. Однако из-за вредных моментов по этой оси (трения, дисбаланса и т.п.) гироскоп начинает «прецессировать» относительно оси ОХ, т.е. ось OZ начинает поворачиваться в направлении оси OY, и гироскоп теряет свойство быть индикатором поворота летательного аппарата.

Явление прецессии следует непосредственно из уравнения (4.1.17), если в нем пренебречь всеми слагаемыми в левой части, кроме последнего слагаемого (так как H>>Jэ, Jвэ, Jв, nα). Прецессию можно измерить, установив на оси ОХ датчик угла. Усилим этот сигнал и подадим его на двигатель, который развивает полезный момент, равный и противоположный по знаку вредному. Тогда прецессия прекратится и гироскоп будет сохранять свои функции.

J э Jвэ cos2 Jв sin 2 Jн 2 Jв J э Jвэ sin cos

na H cos M y

28

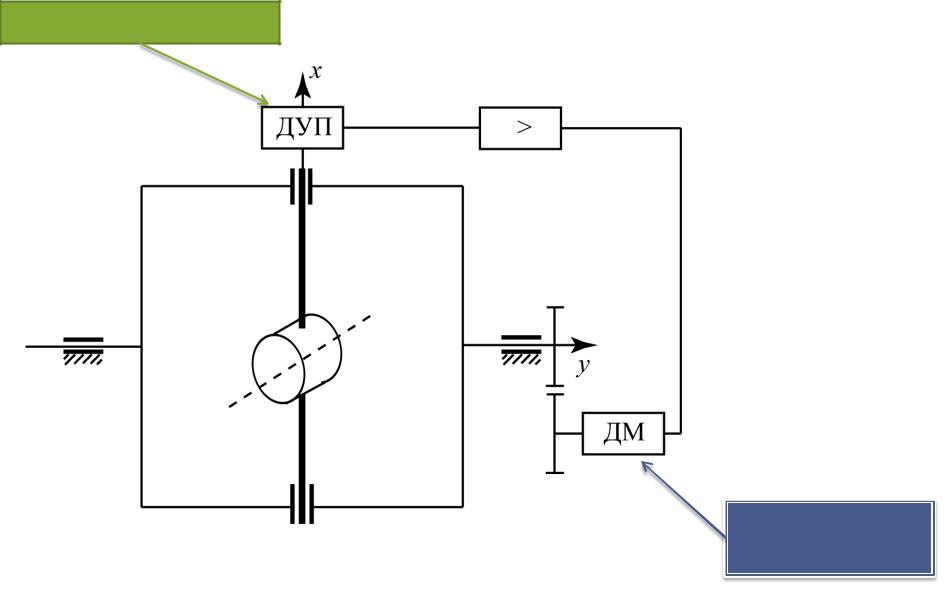
Гироскоп в кардановом подвесе с системой стабилизации угла прецессии называется гирорамой.

датчик угла прецессии

датчик момента (двигатель)

29

Запишем уравнения (4.1.16), (4.1.17) в форме Коши.

Пренебрегая значениями Jэ, Jвэ, Jв по сравнению с Jн, полагая Мх = 0 и вводя обозначения

30