
ОиАС-6
.pdf
1
3. Оптимальные по быстродействию системы управления
Лекция 6.

Качественная сущность проблемы синтеза
2 |
|
Рассмотрим линейный объект управления |
|
x Ax Bu |
(3.1) |
для которого будем искать управление как функцию переменных состояния (фазовых переменных).
Для простоты будем полагать управление скалярным (m=1), ограничение на управление – единичным (u*=1).
Кроме того, не теряя общности рассмотрения, будем считать, что в конечный момент времени фазовая траектория (изображающая точка) должна попасть в начало координат (xi0=0; i=1, …, n).
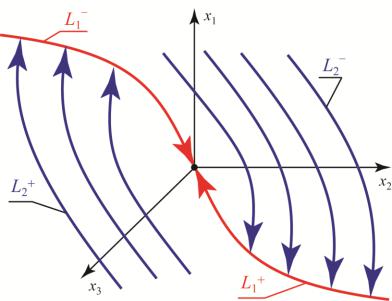
Движение объекта (3.1) при оптимальном по быстродействию программном управлении (лекция 4)
u u* sign n bi1 i t
i 1
описывается уравнениями
|
n |
|
|
|
|
|
|
|
|
|
|
xi |
aij |
xj |
bi1 |
i 1, n |
при |
u 1 |
(3.2) |
||||
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
xi |
aij |
xj |
bi1 |
i 1, n |
при |
u 1 |
(3.3) |
||||
|
j 1 |
|
|
|
|
|
|
|
|
|
|
Траектории, соответствующие решениям этих уравнений, обозначим L+ и L– соответственно.
3
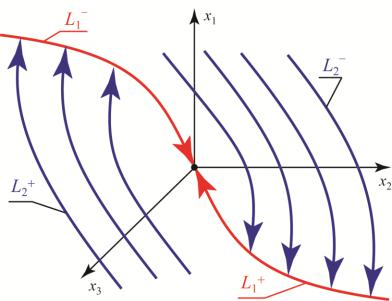
Поскольку оптимальное управление приводит объект в начало координат, то всегда существует такое состояние системы, что кривые L+ и L– проходят через начало координат. Части L1+ и L1– этих кривых (полутраектории), приводящие изображающую точку в начало координат, объединим и обозначим L1. Очевидно, что изображающая точка попадет в начало
координат обязательно по линии L1. Это происходит на последнем интервале оптимального процесса.
В течение оптимального процесса знаки управляющего воздействия чередуются, поэтому концы фазовых траекторий предпоследнего интервала принадлежат кривой L1. Фазовые траектории, соответствующие предпоследнему интервалу и заканчивающиеся на кривых L1+ и L1–, обозначим L2+ и L2–, при этом кривые L2+ заканчиваются на кривой L1–, a L2– – на L1+. Совокупность этих кривых при различных начальных условиях образуют две поверхности, каждая из которых имеет своим краем кривую L1. Обе поверхности стыкуются по линии L1 и образуют поверхность L2, двигаясь по которой изображающая точка попадает на
линию L1 и по ней в начало координат.
4
Продолжая это построение, получим поверхности L3, L4, ..., Ln–1, Ln.
Если характеристический полином объекта имеет действительные корни, то процесс синтеза состоит в отыскании поверхности Ln–1, при этом оптимальный процесс протекает в течение n интервалов (имеет n–1 переключение).
Если начальная точка расположена в области Ln+, то в конце первого интервала фазовая траектория попадает на поверхность Ln–1–, где происходит переключение управляющего воздействия. Далее изображающая точка оказывается на поверхности Ln–2+ и т. д.
К сожалению, эти поверхности описываются трансцендентными уравнениями, и поэтому задача синтеза (построение поверхности переключения Ln–1) решается в замкнутой форме лишь для систем второго и третьего порядка. Для систем более высокого порядка ограничиваются частными решениями либо синтезируют управление, близкое к оптимальному.
5

Синтез оптимальных регуляторов
систем второго порядка
6
Пусть имеется объект управления, описываемый уравнением
y u |
(3.4) |
|u| ≤ u*
Требуется синтезировать управление u u y t , y t , обеспечивающее наискорейшее приведение объекта из произвольного начального состояния в состояние покоя:
y t1 y t1 0 |
(3.5) |
Вводя обозначения y x1 , y x2 , запишем уравнение (3.4) в виде
x1 |
x2 |
(3.6) |
x2 |
u |
(3.7) |
|
|
Функция H1 и сопряженная система имеют в рассматриваемом случае вид
|
|
H1 = ψ1x2 + ψ2u |
(3.8) |
|
|
|
1 |
0 |
(3.9) |
|
|
2 |
1 |
|
|
|
H |
||
Максимум функции H |
1 |
достигается при u u sign |
||
|
|
|
u |
|
|
|
u = l sign ψ2(t). |
||
|
|
(3.10) |
||
Решая систему (3.9), получаем
ψ1(t) = ψ1(t0);
ψ2(t) = – ψ1(t0)(t – t0) + ψ2(t0).
Функция ψ2(t) изменяет знак не более одного раза и это происходит в момент времени
t = ψ2(t0)/ ψ1(t0) + t0. |
(3.11) |
Для решения задачи синтеза оптимального управления построим фазовые траектории системы (3.6), (3.7) и найдем поверхность переключений. Исключая время t из уравнений (3.6), (3.7), поделим первое из них на второе:
7 |
dx1/dx2 = x2/u. |
(3.12) |
|
|
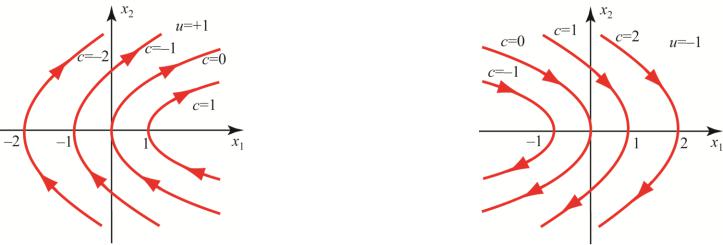
Интегрируя это уравнение при u=const, получим семейство парабол
x1 0,5u 1 x22 |
c |
(3.13) |
или |
|
|
x1 0,5x22 |
c |
(3.14) |
x 0,5x2 c |
(3.15) |
|
1 |
2 |
|
Эти параболы, соответствующие значениям u, равным +1 и –1, приведены на рисунках.
8

Стрелки на параболах означают направление движения при росте t. Проверим указанные на рисунках направления. Пусть u= + 1, тогда из (3.7) получим
x2(t)=t+ x20. |
(3.16) |
Нетрудно видеть, что x2(t) увеличивается с ростом t, а на основе (3.6) заключаем, что x1 увеличивается со временем для тех значений t, при которых x2(t)>0.
При с=0 параболы L |
+ и L – описываются уравнениями |
|
|
|
|
x1 |
x2 |
|
|||
1 |
1 |
|
|
||
|
|
|
|
||
|
x1 0,5x22 ; |
x1 0,5x22 |
|
(3.17) |
|
и проходят через начало координат.
Куски этих парабол, приводящие фазовую траекторию в начало координат, образуют линию переключения, приведенную на рисунке.
9
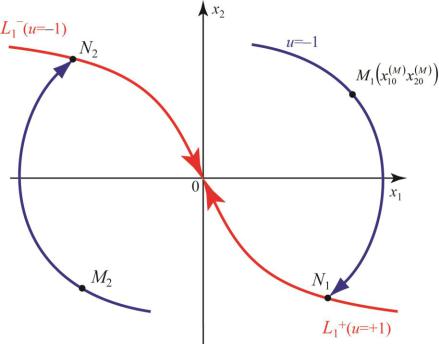
Таким образом, на последнем интервале оптимального процесса изображающая точка попадает в начало координат по кривой L1+ или L1–. Линия L1 делит
D1 |
фазовую плоскость на две области D1 |
и D2, |
|
расположенные над линией L1 и под ней соответственно.
D2 |
Если в начальный момент времени |
|
|
|
изображающая точка находится в области |
|
D1, например в точке M1, то следует |
принять u = –1, тогда фазовая траектория будет двигаться по дуге M1N1 параболы (3.15), проходящей через точку M1. В момент времени, когда изображающая точка попадает в точку N1, необходимо изменить управление на u= + 1. Дальнейшее движение будет происходить по дуге N10. Кривая M1N10 является оптимальной траекторией, соответствующей начальному состоянию .
Аналогично, если в начальный момент времени изображающая точка находилась в области D2, например в точке М2, необходимо принять u= + 1. Изображающая точка будет двигаться по дуге параболы (3.14) и в точке N2 произойдет переключение управления на u=–1.
10
