
методичка лаба термодинамика
.pdfПоскольку в адиабатном процессе теплота к телу не подводится, теплоемкость адиабатного процесса равна нулю (с s = 0).
Удельную теплоемкость можно представить как количество теплоты, которое необходимо подвести к телу, чтобы изменить температуру единицы массы на один градус. Объемная и мольная теплоемкости отличаются от удельной тем, что в первом случае нагревается 1 м 3, во втором - 1кмоль.
Связь между удельной и мольной теплоемкостями
с = с / . |
(4) |
Один киломоль любого газа при нормальных условиях занимает объем 22,4 м 3, следовательно связь между объемной и мольной теплоемкостями
С = с / 22,4. |
(5) |
Связь между объемной и удельной теплоемкостями |
|
С = с , |
(6) |
где - плотность, кг/ м 3.
Зависимость теплоемкости от температуры описывается
зависимостью |
|
с = со + a t + b t2 |
(7) |
Здесь с о - теплоемкость данного газа при 00 С, a, b - постоянные для данного газа величины.
Число членов уравнения (7) выбирается в зависимости от требуемой точности расчета, а также интервала изменения температуры. Для небольших температурных интервалов можно пользоваться постоянными теплоемкостями или применять линейную зависимость
с = со + a t |
(8) |
Наибольший интерес представляют теплоемкости в изобарном и изохорном процессах. В изохорном процессе ввиду
11
постоянства объема работа, совершаемая газом, равна нулю, Вся подведенная в процессе теплота расходуется на изменение внутренней энергии. В изобарном процессе подведенная теплота расходуется на изменение внутренней энергии и совершение работы. С учетом этого имеем
c p = c v + R |
(9) |
Это уравнение называется уравнением Майера. Изобарная теплоемкость больше изохорной теплоемкости на величину удельной газовой постоянной. С учетом последнего показатель адиабаты К, равный
k |
cp |
(10) |
|
cv
всегда больше единицы.
|
|
~ |
|
|
|
4 |
|
10 |
9 |
1 |
|
|
||
|
A |
|
|
|
|
|
5 |
|
|
|
|
V |
|
|
|
6 |
7 |
8 |
|
|
2 |
3 |
|
|
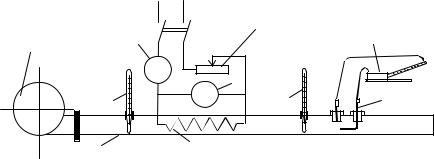
Рис.1 -Экспериментальная установка
Вентилятор 1 нагнетает воздух в трубу 2, в которой установлен электрический нагреватель 3. Мощность электронагревателя измеряется с помощью амперметра 4 (I) и
вольтметра 5 ( U) и регулируется реостатом 10. Для определения температуры воздуха до и после нагревателя служат термометры 6 (Т1) и 7 (Т2). Для измерения расхода воздуха в качестве датчика динамического напора служит пневмометрическая трубка 8.
12
Величина напора (H) определяется микроманометром 9. Измерение атмосферного давления производится барометром.
Порядок проведения эксперимента
1.Измерить диаметр трубы.
2.Включить вентилятор.
3.Включить электронагреватель и выйти на стационарный тепловой режим, о наступлении которого судят по постоянству показаний термометров.
4.Измерить температуры воздуха до нагревателя Т 1
ипосле нагревателя
1.Т 2, падение напряжения U и силу тока I в цепи нагревателя, показания микроманометра Н.
5.При помощи реостата изменить мощность электронагревателя и при очередном стационарном режиме все измерения повторить.
6.При помощи барометра измерить атмосферное
давление.
Таблица измерений
№ пп |
Т1 ,К |
Т2, К |
I, A |
U, B |
H, |
B, кПа |
|
|
|
|
|
кгс/м2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Методика расчета
Объемная изобарная теплоемкость (Дж /норм. м 3 К ) воздуха определяется из выражения
cpm |
|
Q |
, |
(11) |
G |
(T T ) |
|||
|
норм |
2 1 |
|
|
13
где Gнорм - объемный расход воздуха, приведенный к нормальным условиям, норм. м 3/с.
При стационарном тепловом режиме и хорошей изоляции количество теплоты, подведенной к движущемуся воздуху в единицу времени Q , равна мощности электронагревателя (Вт) .
Q = U |
I |
|
|
|
|
|
|
|
|
(12) |
|
Объемный расход |
воздуха |
при |
нормальных |
условиях |
|||||||
(норм.м3/с) определяется по формуле |
|
|
|
|
|
||||||
Gнорм wcp |
d2 |
|
|
B |
|
273 |
, |
(13) |
|||
4 |
|
760 |
|
T |
|||||||
|
|
||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
где d- диаметр трубы, м,
w ср - средняя скорость воздуха, м/с, В - атмосферное давление, мм рт. ст.
Для того чтобы определить среднюю скорость воздуха, надо сначала найти осевую скорость (скорость на оси трубы). Для этого воспользуемся показаниями микроманометра, соединенного с
пневмометрической |
трубкой, установленной |
по оси трубы, |
регистрирующего динамический напор |
|
|
Pдин = 9,81 Н К, Па |
(14) |
|
Здесь Н - отсчет по шкале микроманометра, кгс/м 2, К - постоянная прибора( микроманометра),
9,81 - множитель для перевода значений давления из кгс/м 2
в Па.
Осевая скорость (м/с) определяется |
|
||||
w |
|
2pдин |
|
, м/c , |
(15) |
|
|||||
0 |
|
|
|
||
|
|
|
|||
где - плотность воздуха, определяется по таблице физических свойств воздуха по температуре Т2.
Средняя скорость определяется при известной осевой скорости из соотношения
14
|
|
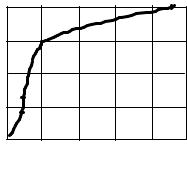
w ср = а w 0 ,м/c |
|
||
а |
|
|
|
|
|
0,8 |
|
|
|
|
|
0,7 |
|
|
|
|
|
0,6 |
|
|
|
|
|
0,5 |
|
|
|
|
|
3 |
4 |
5 |
6 |
7 |
lg Re |
Сначала определяется число Рейнольдса |
|||||
(16)
где а - скоростной коэффициент, определяемый по графической зависимости от числа Рейнольдса, характеризующего режим течения,
a = f (Re) .
Re |
wod |
(17) |
|
Здесь d - диаметр трубы, м
- кинематический коэффициент вязкости воздуха, определяется по таблице физических свойств воздуха по температуре Т2, м 2 /с.
Обработка результатов измерений
Количество теплоты, подведенной к воздуху, определяется по формуле (12). По формулам (14) и (15) находится осевая скорость воздуха. По формуле (17) рассчитывается число Рейнольдса. По графику (рис.) определяется скоростной коэффициент и далее средняя скорость по формуле (16). расчет расхода воздуха при нормальных условиях производится по зависимости (13). Средняя объемная изобарная теплоемкость воздуха определяется по формуле (11). Воспользовавшись формулами (4),(5), (6) следует рассчитать мольную и удельную теплоемкости воздуха (изохорную и изобарную), а по формуле (10) - показатель адиабаты
15
Оценка точности измерений
Относительная погрешность определения средней объемной изобарной теплоемкости воздуха определяется по формуле
С pm =( I/I)+ ( U /U) + ( T / T) +( 2 T/ (T2 - T1))+ +(0.5 H/H)
Лабораторная работа №3
ИЗУЧЕНИЕ ТЕРМОДИНАМИЧЕСКИХ ПРОЦЕССОВ В ИДЕАЛЬНОМ ГАЗЕ
Цель работы: Изучение процессов изменения состояния идеального газа. Pасчет процессов в идеальном газе. Построение по полученным данным процессов в термодинамических p,v- и T,s- диаграммах Опытное определение отношения теплоемкостей (показателя адиабаты Пуассона).
Основные сведения:
Показатель адиабаты является важной термодинамической характеристикой вещества, необходимой для проведения расчета адиабатного процесса
PV k = const. |
(1) |
Адиабатный процесс - процесс изменения состояния газа, происходящий без теплообмена с окружающей средой.
Показатель адиабаты может быть определен по таблицам для различных газов в зависимости от параметров состояния.
Для идеального газа показатель адиабаты не зависит от параметров состояния, а является молекулярной функцией (зависит от атомности газа)
16
|
k cp |
|
5 R |
|
|
|
|
|
2 |
|
|
(2) |
|
|
c |
|
3 |
R |
|
|
|
v |
|
2 |
|
|
|
|
|
|
|
|
|
|
где - число степеней свободы вращательного движения молекул. |
||||||
Методика экспериментального определения |
||||||
|
показателя адиабаты. |
|
|
|||
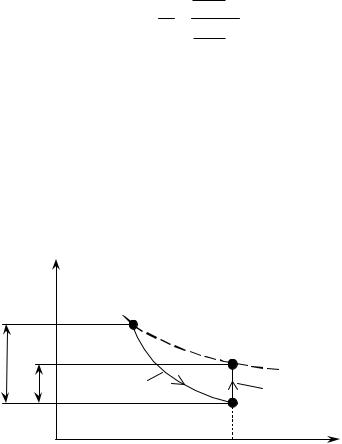
На рис. 1 в P,V- диаграмме представлены два последовательных |
||||||
процесса изменения состояния системы: адиабатное расширение (1- |
||||||
2), а затем нагрев при постоянном объеме (2-3) газа до |
||||||
первоначальной температуры. |
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
Н1 |
|
|
|
3 |
Т1 |
= const |
|
|
|
|
|||
|
|
|
|
|
|
|
Н2 |
dq = 0 |
|
|
|
V = const |
|
|
|
|
|
2 |
|
|
|
|
|
V2 = V3 |
|
V |
|
|
Рис. |
1 |
|
|
|
|
В адиабатном процессе 1-2 изменение параметров выражается |
||||||
зависимостью |
|
|
|
|
|
|
|
|
|
|
|
|
17 |
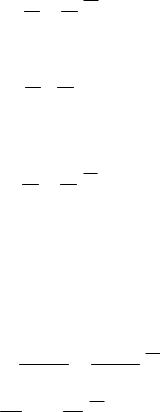
T1 (P1 )kk1
T2 P2
Для изохорного процесса 2-3
T3 P3
T2 P2
Поскольку Т 1 = Т 3, из уравнений (3) и (4) имеем
P3 (P1 )kk1
P2 P2
Обозначим
Р3 = Р 2 + Н 2
Р1 = Р 2 + Н 1
Разделим обе части уравнения (5) на Р2, получим
P2 H2 (P2 H1 )kk1
P2 P2
1 H2 (1 H1 )kk1
P2 P2
Давление Р 2 - атмосферное.
Р 2 = В 10 5 Па
Воспользуемся известным разложением:
(3)
(4)
(5)
(6)
(7)
(8)
ln(1 X) X |
X2 |
|
X |
3 |
... ( 1) |
n 1 |
Xn |
|
|
|
|
|
|
(9) |
|||
|
|
|
|
|
||||
2 |
3 |
|
|
|
n |
|||
для логарифмирования выражения (8). При этом ограничимся лишь первым членом разложения, что при соответствующем Н 1 дает ошибку лишь в 4 знаке.
18
KH2 |
(K 1) |
H1 |
(10) |
|
P2 |
P2 |
|||
|
|
В итоге получаем выражение
k |
H1 |
(11) |
|
H1 H2
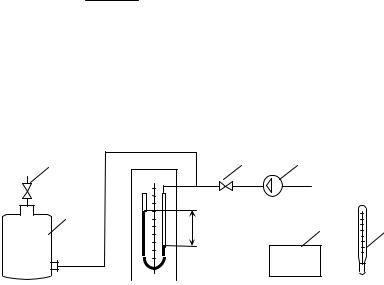
1 - стеклянный сосуд, 2,4 - краны, 3 - дифференциальный манометр, 5 – насос , 6- барометр, 7- термометр
2 |
4 |
5 |
|
1 |
|
6 |
7 |
Н |
|
3 
Рис.2 - Схема экспериментальной установки
Стеклянный сосуд 1 соединен с U - образным дифференциальным стеклянным манометром 3 и снабжен двумя двухходовыми кранами 2 и 4. Воздух в сосуд подается насосом 5. В качестве модели идеального газа в установке используется атмосферный воздух.
Равенство температур перед адиабатным расширением и в конце изохорного нагрева (тч. 1 и 3 на рис. 1) удобно получать, добиваясь теплового равновесия с окружающей средой. Наступление равновесия контролируется по постоянству давления в системе.
19
Порядок проведения работы
1.Измеряется атмосферное давление и температура.
2.В начальном состоянии (тч. 0 на рис. 3) в баллоне
находится воздух при температуре Т о и давлении Р о = В, т.е. при тепловом равновесии с окружающей средой.
3.Закрывается кран 2 и при открытом кране 4 воздух насосом нагнетается в сосуд.
Не следует стремиться получить давление выше 600 мм в. ст., т.к. можно выдавить воду из дифманометра.
4.Закрывается кран 4 и фиксируется Н о ( рис. 3). При этом абсолютное давление
Р1 = В + Н о.
5.После прекращения падения давления в сосуде, которое
будет происходить сразу после закрытия крана 4, регистрируется давление Н 1 (рис. 3). При этом абсолютное давление
Р 2 = В +Н1.
6. Открывается кран 2 и как только давление газа в баллоне упадет до атмосферного и уровни водяных столбов в дифманометре выровняются, кран 2 закрывается. Процесс 2-3 будет адиабатным лишь в том случае, если он проводится достаточно быстро . В этом случае Р 3 = В (рис. 3).
7. После закрытия крана 2 начинает расти давление, измеряется Н2 (рис. 3). В этом случае Р 4 = В + Н 2.
Таблица измерений
№ |
В |
Т о К |
Но , |
Н1 |
Н 2, |
К |
n |
п.п |
кПа |
|
мм |
мм |
мм |
|
|
|
|
|
в.ст., |
в.ст., |
в.ст. , |
|
|
|
|
|
Па |
Па |
Па |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20
