
- •Оглавление
- •1. Законы постоянного тока
- •2. Постоянный ток в проводящей среде
- •3. Магнитное поле постоянного тока
- •4. Силы, действующие на движущиеся заряды в магнитном поле
- •5. Закон полного тока. Магнитный поток. Магнитные цепи
- •6. Работа по перемещению проводника с током в магнитном поле. Электромагнитная индукция. Индуктивность
- •Примеры решения задач
- •7. Энергия магнитного поля Основные формулы
- •Примеры решения задач
4. Силы, действующие на движущиеся заряды в магнитном поле
Основные формулы
• Закон Ампера. Сила, действующая на проводник с током в магнитном поле,
F=[l B] I
где I – сила тока; l – вектор, равный по модулю длине l проводника и совпадающий по направлению с током; В – магнитная индукция поля.
Модуль вектора F определяется выражением
F= B I l sin
где α – угол между векторами I и В.
• Сила взаимодействия двух прямых бесконечно длинных параллельных проводников с токами I1иI2, находящихся на расстоянииd друг от друга, рассчитанная на отрезок проводника длинойl выражается формулой
F=0I1I2l/2πd/
• Магнитный момент контура с током
pm=I S
где S – вектор, равный по модулю площади S, охватываемой контуром, и совпадающий по направлению с нормалью к его плоскости.
• Механический момент, действующий на контур с током, помещенный в однородное магнитное поле,
M=[pm B].
Модуль механического момента
M=pmB sin,
где α – угол между векторами рm и В.
Потенциальная (механическая) энергия контура с током в магнитном поле
Пмех= pm B = pmBcosα.
Сила, действующая на контур с током в магнитном поле (изменяющемся вдоль оси x),
F=pm∂B/∂хcosα,
где ∂B/∂х–изменение магнитной индукции вдоль осиОх, рассчитанное на единицу длины; α–угол между векторамирmиВ.
Сила F, действующая на зарядQ, движущийся со скоростьюv в магнитном поле с индукциейВ (сила Лоренца), выражается формулой
F=Q [v B] илиF=|Q|B sin,
где –угол, образованный вектором скоростиv движущейся частицы и векторомВ индукции магнитного поля.
Примеры решения задач
Пример 4.1. По двум параллельным прямым проводам длиной l=2,5 м каждый, находящимся на расстоянии d=20 см друг от друга, текут одинаковые токи I=1 кА. Вычислить силу F взаимодействия токов.
Решение. Взаимодействие двух проводников, по которым текут токи, осуществляется через магнитное поле. Каждый ток создает магнитное поле, которое действует на другой проводник. Предположим, что оба тока (обозначим их 1г и I2) текут в одном направлении.
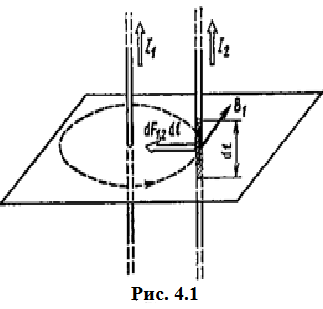
Вычислим силу F1,2, с которой магнитное поле, созданное током I1, действует на проводник с током I2. Для этого проведем магнитную силовую линию так (штриховая линия на рис. 4.1), чтобы она касалась проводника с током I2. По касательной к силовой линии проведем вектор магнитной индукции В1. Модуль магнитной индукции B1 определяется соотношением
 (1)
(1)
Согласно закону Ампера, на каждый элемент второго проводника с током I2 длиной dl2 действует в магнитном поле сила (длинный проводник (l>>d) можно приближенно рассматривать как бесконечно длинный)
![]()
Так как отрезок dl
перпендикулярен
вектору B1,
то
![]() и
тогда
и
тогда
![]() (2)
(2)
Подставив в выражение (2) В1 из (1), получим
![]()
Силу F1,2 взаимодействия (по третьему закону Ньютона, сила, действующая на первый проводник со стороны второго, будет равна найденной по модулю и противоположной по направлению) проводников с током найдем интегрированием по всей длине второго проводника;
![]()
Заметив, что I1=I2=I
и l2=l,
получим
![]()
Убедимся в том, что правая часть этого равенства дает единицу силы
![]()
Произведем вычисления:
![]()
Сила F1,2 сонаправлена с силой dF1,2 (рис. 4.1) и определяется (в данном случае это проще) правилом левой руки.
Пример 4.2. Провод в виде тонкого полукольца радиусом R=10 см находится в однородном магнитном поле (B=50 мТл). По проводу течет ток I=10 А. Найти силу F, действующую на провод, если плоскость полукольца перпендикулярна линиям магнитной индукции, а подводящие провода находятся вне поля.
Решение.
Расположим провод в плоскости чертежа
перпендикулярно линиям магнитной
индукции (рис. 4.2) и выделим на нем малый
элемент dl
с током. На этот элемент тока Idl
будет действовать по
закону Ампера сила dF=I[dlB].
Направление этой силы можно определить
по правилу векторного произведения или
по правилу левой руки.
Используя симметрию, выберем координатные оси так, как это изображено на рис. 4.2. Силу dF представим в виде
![]()
где i и j – единичные векторы (орты); dFx и dFy — проекции вектора dF на координатные оси Ох и Оу.
Силу F, действующую на весь провод, найдем интегрированием:
![]()
где символ L
указывает на то, что
интегрирование ведется по всей длине
провода L.
Из соображений симметрии первый интеграл
равен нулю
 тогда
тогда
![]() (1)
(1)
Из рис. 4.2 следует, что
![]()
где dF
–
модуль вектора![]() Векторdl
перпендикулярен вектору
Векторdl
перпендикулярен вектору
![]() то
то
![]() Выразив длину дуги
dl
через радиус R
и
угол α, получим
Выразив длину дуги
dl
через радиус R
и
угол α, получим
![]()
Тогда
![]()
Введем dFy под интеграл соотношения (1) и проинтегрируем в пределах от -π/2 до +π/2 (как это следует из рис. 4.2):
![]()
Из полученного выражения видно, что сила F сонаправлена с положительным направлением оси Оу (единичным вектором j).
Найдем модуль силы F:
![]()
Убедимся в том, что правая часть этого равенства дает единицу силы (Н):
![]()
Произведем вычисления:
![]()
Пример 4.3. На проволочный виток радиусом r=10 см, помещённый между полюсами магнита, действует максимальный механический момент Мmax=6,5 мкН. Сила тока I в витке равна 2А. Определить магнитную индукцию В поля между полюсами магнита. Действием магнитного поля Земли пренебречь.
Решение. Индукцию В магнитного поля можно определить из выражения механического момента, действующего на виток с током в магнитном поле,
![]() (1)
(1)
Если учесть, что максимальное значение механический момент принимает при α=π/2 (sin α=l), а также что pm=IS, то формула (1) примет вид
![]()
Отсюда, учитывая, что S=πr2, находим
![]() (2)
(2)
Произведя вычисления по формуле (2), найдем
В=104 мкТл.
Задача 4.1
|
Вариант № |
l, м |
d, см |
Ток I, кА |
|
1 |
3,07 |
20,6 |
1,11 |
|
2 |
2,96 |
23,5 |
1,38 |
|
3 |
2,67 |
20,6 |
1,14 |
|
4 |
2,98 |
20,3 |
1,96 |
|
5 |
2,56 |
24 |
1,07 |
|
6 |
2,55 |
20,1 |
1,33 |
|
7 |
2,74 |
22,7 |
1,06 |
|
8 |
3,47 |
21,2 |
1,57 |
|
9 |
2,73 |
20,8 |
1,5 |
|
10 |
3,09 |
21,8 |
1,2 |
|
11 |
2,98 |
21,7 |
1,08 |
|
12 |
3,37 |
22,4 |
1,91 |
|
13 |
2,56 |
22,5 |
1,66 |
|
14 |
2,6 |
22,4 |
1,32 |
|
15 |
2,63 |
22 |
1,9 |
|
16 |
2,54 |
24 |
1,8 |
|
17 |
3,33 |
23,9 |
1,75 |
|
18 |
3,22 |
21,8 |
1,14 |
|
19 |
2,95 |
23,7 |
1,83 |
|
20 |
2,89 |
22,4 |
1,37 |
|
21 |
3,27 |
23,9 |
1,78 |
|
22 |
2,67 |
20,9 |
1,88 |
|
23 |
2,9 |
20,8 |
1,03 |
|
24 |
2,98 |
22,4 |
1,04 |
|
25 |
2,74 |
21 |
1,03 |
|
26 |
3,09 |
23,5 |
1,47 |
|
27 |
2,98 |
20,2 |
1,27 |
|
28 |
3,05 |
22,9 |
1,8 |
|
29 |
2,74 |
20,4 |
1,27 |
|
30 |
2,57 |
20,4 |
1,71 |
Задача 4.2
|
Вариант № |
R, см |
B, мТл |
Ток I, А |
|
1 |
10,6 |
50,3 |
11,2 |
|
2 |
10,7 |
52,4 |
11,2 |
|
3 |
11,7 |
51 |
11,3 |
|
4 |
10,7 |
50,6 |
12 |
|
5 |
11,2 |
50,3 |
11,8 |
|
6 |
10,9 |
51,3 |
10,1 |
|
7 |
10,5 |
53,6 |
11,6 |
|
8 |
10,6 |
53,5 |
10,3 |
|
9 |
11,5 |
53,9 |
12 |
|
10 |
10,5 |
52,8 |
12,2 |
|
11 |
10,1 |
54,2 |
10,6 |
|
12 |
10,7 |
53,9 |
10,7 |
|
13 |
10 |
50,5 |
11,2 |
|
14 |
11,9 |
51,5 |
12,7 |
|
15 |
11,7 |
54,3 |
12,8 |
|
16 |
10,4 |
54,2 |
11,7 |
|
17 |
10,8 |
50,8 |
11,3 |
|
18 |
11,3 |
50,4 |
11,6 |
|
19 |
10,6 |
51,4 |
11,1 |
|
20 |
11,2 |
52,8 |
12,2 |
|
21 |
11,2 |
50,6 |
11,6 |
|
22 |
10,7 |
50,3 |
11,7 |
|
23 |
10,1 |
53,5 |
11,9 |
|
24 |
10,3 |
51,5 |
10,8 |
|
25 |
10,1 |
53 |
10,4 |
|
26 |
10,6 |
52,7 |
12,8 |
|
27 |
11,8 |
53,1 |
12,8 |
|
28 |
11,4 |
50,8 |
10,9 |
|
29 |
11,8 |
54,1 |
11,2 |
|
30 |
11,5 |
51 |
12,6 |
Задача 4.3
|
Вариант № |
r, см |
Ток I, А |
Мmax, мкН |
|
1 |
14,1 |
4,3 |
6,5 |
|
2 |
12,7 |
2,9 |
6,1 |
|
3 |
12,4 |
2,2 |
6,3 |
|
4 |
14,1 |
2,1 |
6,1 |
|
5 |
13,8 |
4,3 |
6,6 |
|
6 |
11,2 |
2,8 |
6,9 |
|
7 |
12,8 |
4,4 |
6,4 |
|
8 |
10 |
3,2 |
6,6 |
|
9 |
12,7 |
3,8 |
6,3 |
|
10 |
11,2 |
3,2 |
6,6 |
|
11 |
11,6 |
3 |
6,2 |
|
12 |
11 |
3 |
6,8 |
|
13 |
14,8 |
4 |
6,7 |
|
14 |
14,2 |
3,1 |
6,6 |
|
15 |
10,4 |
2,3 |
6,2 |
|
16 |
11,8 |
2,3 |
6,8 |
|
17 |
14,6 |
3,2 |
6,7 |
|
18 |
12,9 |
2,3 |
6,1 |
|
19 |
10,7 |
3,8 |
6,8 |
|
20 |
12,4 |
2,7 |
6,4 |
|
21 |
10,9 |
3 |
6,1 |
|
22 |
11,3 |
4,1 |
6,4 |
|
23 |
13 |
3,5 |
6,5 |
|
24 |
12,3 |
3,3 |
6,0 |
|
25 |
12,8 |
3,7 |
6,2 |
|
26 |
12,3 |
4,3 |
6,0 |
|
27 |
10,2 |
2,7 |
6,5 |
|
28 |
13,7 |
4,3 |
6,6 |
|
29 |
10,5 |
2,3 |
6,2 |
|
30 |
11,8 |
3,2 |
6,8 |
