3. Магнитное поле постоянного тока

Основные формулы

 Закон Био – Савара – Лапласа

dB=₀dl r I/4π r,

где dB – магнитная индукция поля, создаваемого элементом i проводника с током;  – магнитная проницаемость; ₀ – магнитная постоянная (₀ =4 10 ^-7 Гн/м); dl – вектор, равный по модулю длине dl проводника и совпадающий по направлению с током (элемент проводника); I – сила тока; r – радиус-вектор, проведенный от середины элемента проводника к точке, магнитная индукция в которой определяется.

Модуль вектора dB выражается формулой

dB=₀ dl I sin α/4π r²,

где  – угол между векторами dl и r.

 Магнитная индукция В связана с напряженностью Н магнитного поля (в случае однородной, изотропной среды) соотношением

или в вакууме

 Магнитная индукция в центре кругового проводника с током

где R — радиус кривизны проводника.

 Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током,

где r – расстояние от оси проводника.

Магнитная индукция поля, создаваемого отрезком проводником

Обозначения ясны из рис. 3.1, а). Вектор индукции В перпендикулярен плоскости чертежа, направлен к нам и поэтому изображен точкой.

При симметричном расположении концов проводника относительно точки, в которой определяется магнитная индукция (рис. 3.1, б),и, следовательно,

 Магнитная индукция поля, создаваемого соленоидом в средней его части (или тороида на его оси),

где п — число витков, приходящихся на единицу длины соленоида; I – сила тока в одном витке.

 Принцип суперпозиции магнитных полей: магнитная индукция В результирующего поля равна векторной сумме магнитных индукций В₁, В₂, ..., В_n складываемых полей, т. е.

В частном случае наложения двух полей

а модуль магнитной продукции

где  – угол между векторами В₁ и В₂.

Примеры решения задач

Пример 3.1. Два параллельных бесконечно длинных провода, по которым текут в одном направлении токи I=60 А, расположены на расстоянии d=10 см друг от друга. Определить магнитную индукцию В в точке, отстоящей от одного проводника на расстоянии г₁=5 см и от другого – на расстоянии r₂=12 см.

Решение. Для нахождения магнитной индукции в указанной точке А (рис. 3.2) определим направления векторов индукций В₁ и В₂ по лей, создаваемых каждым проводником в отдельности, и сложим их геометрически, т. е. B=B₁+B₂. Модуль индукции найдем по теореме косинусов:

(1)

Значения индукций Bi и В₂ выражаются соответственно через силу тока I и расстояния r₁ и r₂ от провода до точки, индукцию

в которой мы вычисляем: 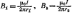ПодставляяB₁ иВ₂ в формулу (1) и вынося 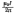за знак корня, получим

(2)

Убедимся в том, что правая часть этого равенства дает единицу магнитной индукции (Тл):

Здесь мы воспользовались определяющей формулой для магнитной индукции (В=М_mак /р_п). Откуда следует, что

Вычисляем cos. Заметим, что =∠DAC. Поэтому по теореме косинусов запишем , гдеd – расстояние между проводами. Отсюда

Подставив данные, вычислим значение косинуса: cos  = 0,576.

Подставив в формулу (2) значения ₀, I, r₁, r₂ и cos , найдём В=286 мкТл.

Пример 3.2. По двум длинным прямолинейным проводам, находящимся на расстоянии r=5 см друг от друга в воздухе, текут токиI₁=10 А, I₁=10 А. Определить магнитную индукциюВ поля, создаваемого токами в точке а=0,5r от левого провода, т. е. лежащей посередине между проводами, для случаев: 1) провода параллельны, токи текут в одном направлении (рис. 3.3, а); 2) провода параллельны, токи текут в противоположных направлениях (рис. 3.3, б); 3) провода перпендикулярны, направление токов указано на рис. 3.3, в, в этом случае точка а лежит на диагонали прямоугольника.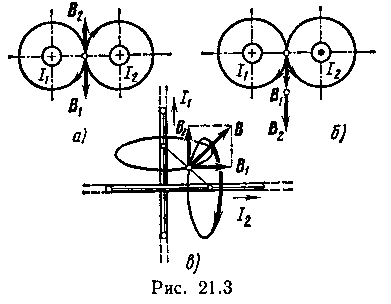

Рис 3.3

Решение: Результирующая индукция магнитного поля равна векторной сумме: B=B₁+B₂, где B₁ – индукция поля,создаваемого током I₁; В₂ – индукция поля создаваемого током I₂.

Если B₁ и В₂ направлены по одной прямой, то векторная сумма может быть заменена алгебраической суммой:

В=В₁+В₂. (1)

При этом слагаемые В₁ и В₂ должны быть взяты с соответствующими знаками.В данной задаче во всех трех случаях модули индукций В₁ и В₂ одинаковы, так как точки выбраны на равных расстояниях от проводов, по которым текут равные токи. Вычислим эти индукции по формуле

B₁=₀I₁/(2r), B₂=₀I₂/(2r). (2)

Подставив значения величин в формулу (2), найдем модули В₁ и В₂:

В₁=В₂=80 мкТл.

1-й случай. Векторы B₁ и В₂ направлены по одной прямой (рис. 3.3, а); следовательно, результирующая индукция В определяется по формуле (1). Приняв направление вверх положительным, вниз – отрицательным, запишем: В₁=-80 мкТл, В₂=80 мкТл.

Подставив в формулу (1) эти значения В₁ и B₂, получим

В=В₁+В₂=0.

2-й случай. Векторы В₁ и В₂ направлены по одной прямой в одну сторону (рис. 3.3, б). Поэтому можем записать

В₁=В₂=-80 мкТл.

Подставив в формулу (1) значения B₁ и В₂ получим

В=В₁+В₂=-160 мкТл.

3-й случай. Векторы индукций магнитных полей, создаваемых токами в точке, лежащей посередине между проводами, взаимно перпендикулярны (рис. 3.3, в). Результирующая индукция по модулю и направлению является диагональю прямоугольника, построенного на векторах В₁ и В₂. По теореме Пифагора найдем

(3)

Подставив в формулу (3) значения В₁ и В₂ и вычислив, получим Рис. 3.4B =113 мкТл.

Пример 3.3. Определить магнитную индукцию В поля, создаваемого отрезком бесконечно длинного прямого провода, в точке, равноудаленной от концов отрезка и находящейся на расстоянии r₀=20 см от середины его (рис. 3.4). Сила тока I, текущего по проводу, равна 30 А, длина l отрезка равна 60 см.

Решение. Для определения магнитной индукции поля, создаваемого отрезком провода, воспользуемся законом Био –Савара–Лапласа:

(1)

Прежде чем интегрировать выражение (1), преобразуем его так, чтобы можно было интегрировать по углу . Выразим длину элемента dl проводника через d. Согласно рис. 3.4, запишем

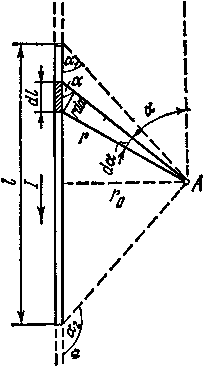
Рис. 3.4

Подставим это выражение dl в формулу (1):

Но r – величина переменная, зависящая от  и равная 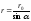Подставив r в предыдущую формулу, найдем

(2)

Чтобы определить магнитную индукцию поля, создаваемого отрезком проводника, проинтегрируем выражение (2) в пределах от ₁ до ₂:

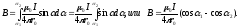(3)

Заметим, что при симметричном расположении точки A относительно отрезка провода cos ₂= – cos ₁. С учетом этого формула (3) примет вид

(4)

Из рис. 3.4следует

Подставив выражение cos ₁ в формулу (4), получим

(5)

Подставим числовые значения в формулу (5) и произведем вычисления:

Задача 3.1

Вариант №	Ток I, А	d, см	г1, см	r2, см
1	67,5	10,8	7,06	15,4
2	67,1	12,6	9,95	15,4
3	70,1	10	9,22	12,6
4	69,8	13,6	8,03	15,1
5	61,7	11,9	8,78	14,8
6	70,2	12,6	9,53	12,2
7	71,8	12,2	9	12,2
8	70,7	12,3	8	15,3
9	63,6	10,7	5,71	14,7
10	69,8	11,2	7,24	13,5
11	71,7	10,2	6,09	12,3
12	64,1	13,2	7,94	14,3
13	71,1	10,9	9,55	14,4
14	64	13,6	9,54	15,5
15	62,2	11,5	6,3	12,6
16	62,6	10,8	6,24	16,8
17	66,7	12,2	5,66	16,6
18	71,2	11,5	7,79	17
19	60,8	12,8	6,1	12,3
20	64,9	12,2	5,71	13,9
21	70,2	11	9,75	12,8
22	69,4	10,4	7,23	12,2
23	61,8	12,3	9,69	16,3
24	71,7	12,8	8,15	12,8
25	61,8	12,5	5,1	16
26	62,9	13,6	7,22	14,8
27	67,9	10,7	6,92	13,1
28	61,8	12,9	9,18	14,5
29	71,4	12,1	7,36	14,3
30	60,5	13,4	5,34	16,5

Задача 3.2

Вариант №	r, см	Ток I1, А	Ток I2, А	Точка а
1	7,06	11,25	15,51	0,83
2	7,04	10,8	16,03	0,79
3	6,26	12	15,23	0,63
4	7,83	11,12	15,28	0,83
5	7,14	11,59	15,06	0,57
6	7,32	10,3	17,94	0,78
7	6,68	11,96	17,59	0,75
8	7,87	10,98	16,07	0,54
9	7,72	10,89	17,83	0,51
10	7,22	10,13	17,86	0,74
11	6,63	11,16	17,36	0,79
12	6,44	10,95	15,91	0,77
13	7,99	10,08	15,79	0,68
14	6,05	10,48	17,28	0,56
15	7,12	11,89	16,79	0,62
16	7	10,06	17,16	0,56
17	6,07	10,72	16,6	0,53
18	7,02	11	16,32	0,52
19	6,68	11,63	15,46	0,69
20	6,03	11,74	17,07	0,63
21	6,88	10,47	15,56	0,64
22	6,73	11,5	15,99	0,53
23	6,28	10,56	16,26	0,54
24	7,91	11,33	17,48	0,78
25	6,48	10,74	15,04	0,81
26	6,71	11,86	16,09	0,54
27	6,64	10,41	15,72	0,76
28	6,44	10,61	15,94	0,61
29	7,86	10,97	15,62	0,69
30	6,47	10,86	16,53	0,7

Задача 3.3

Вариант №	r, см	Ток I, А	l, см
1	23,7	32,4	66
2	23,5	38	68,8
3	24,2	38,5	64,8
4	23,4	38,4	62,6
5	20,4	33,5	68,7
6	20,5	36,4	60,7
7	24,6	31,1	62,9
8	20,3	36,9	70
9	21	34,7	61
10	22,6	31,1	62,9
11	24,6	33,8	68,3
12	24	33,1	65,7
13	21,6	30,9	63,3
14	24	33,1	69,3
15	22	36,2	69,9
16	20,7	36,9	63,7
17	23,1	32,4	67,2
18	22,1	38,2	68,4
19	24,6	32,9	65,8
20	22	36,5	69,2
21	20,8	31,6	61,3
22	20,5	40	60,8
23	21,8	35,1	61,1
24	21,5	33,5	65,4
25	24,8	35,8	64,2
26	24,8	32,5	66
27	22,1	34,9	65,3
28	20,7	33,2	64,2
29	20,9	31,8	67,8
30	20,1	34,9	64,4