Порядок выполнения работы

1. Снять грузы mс диска.

2. Повернуть крутильный маятник на угол порядка 5-10и, предоставив систему самой себе, привести ее в колебательное движение. По секундомеру отсчитать времяп= 10 полных колебанийt₁. Повторить операцию 5 раз.

3. Поместить на диск два цилиндра, линейкой измерить расстояние lмежду их осями вращения.

4. Штангенциркулем измерить диаметр одного из цилиндров.

5. Выполнить пункт 2 для крутильного маятника с цилиндрами.

6. Результаты измерений и погрешности измерительных приборов занести в таблицу.

7. Произвести математическую обработку результатов измерений, найти по формуле (7) момент инерции маятника , а также его погрешность.

Таблица измерений

n	t1, c	t2, c	t, c	l, мм	l, мм	d, мм	d, мм	m, кг

Контрольные вопросы

1. Дайте определение момента инерции материальной точки и твердого тела.

2. Сформулируйте теорему Штейнера, приведите пример ее применения.

3. Какие деформации называются упругими?.

4. Сформулируйте и запишите закон Гука применительно к деформациям кручения и сдвига.

5. Какой физический смысл модуля кручения и модуля сдвига?

6. Выведите расчетную формулу.

Лабораторная работа 4-2 определение модулей сдвига и кручения методом крутильных колебаний

Цель работы: с помощью крутильного маятника определить модули кручения и сдвига проволоки.

Приборы и принадлежности: крутильный маятник, секундомер, штангенциркуль, линейка.

Методика и техника эксперимента

Крутильный маятник представляет собой упругий стержень, один конец которого закреплен, а к другому прикреплено массивное тело таким образом, что его центр инерции находится на оси стержня ОО₁.

Если тело повернуть на небольшой угол вокруг осиОО₁ и предоставить самому себе, то оно начнет совершать крутильные колебания.

Можно показать, что величина периода крутильных колебаний Т зависит от упругих свойств проволоки и момента инерции маятника.

Если на тело действует пара сил, то численное значение вращающего момента по основному закону вращательного движения

,

где: - угловое ускорение;J – момент инерции маятника относительно оси ОО₁.

Момент упругих сил, возникающих в образце при кручении, по закону Гука равен

,

где D - модуль кручения. Поэтому

.

Последнее уравнение представляет собой дифференциальное уравнение крутильных колебаний. Его можно привести к виду:

.

Как нетрудно увидеть путем прямой подстановки, решение данного уравнения имеет вид:

,

т.е. угол  изменяется по гармоническому закону, тело совершает гармонические колебания с циклической частотой и периодом

. (1)

Виспользуемой экспериментальной установке к нижнему концу вертикально висящей проволокиСD прикрепляется горизонтальный стержень AB со средним грузом M и двумя равными перемещаемыми грузами т. Если на концы стержня AB подействовать парой сил, создающей вращающий момент, а затем систему предоставить самой себе, то она будет совершать крутильные колебания в горизонтальной плоскости.

В основе данной работы лежит соотношение (1), в котором J - момент инерции системы относительно осп СD, D - модуль кручения, T - период крутильных колебаний.

Модуль кручения D можно определить, не зная момента инерции всей системы J относительно оси СD, но зная моменты инерции относительно СD небольших по объему массивных грузов т, располагая их на минимальном l₁ и максимальном l₂ расстояниях. Обозначая периоды колебаний маятника для этих двух случаев Т₁ и Т₂, получим из выражения (1):

, .

Вычтем из второго равенства первое

и выразим отсюда

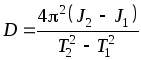. (2)

Принимая грузы m за материальные точки, моменты инерции системы J₁ и J₂ можно найти как

, , (3)

где J₀ – момент инерции стержня со средним грузом. Подставляя (3) в (2), получаем:

.

Выражая периоды Т₁ и Т₂ через время t₁ и t₂ n колебаний при расположении грузов m на расстояниях соответственно l₁ и l₂

, ,

получаем расчётную формулу для модуля кручения материала проволоки маятника

. (4)

Поскольку деформации кручения являются частным случаем сдвиговых деформаций, модуль кручения связан с модулем сдвига соотношением:

, (5)

где: d– диаметр проволокиСD;L– её длина.