5. Изучение упругих cboйсtb твердых tEл Лабораторная работа 4.1 Определение модуля упругости из растяжения проволоки на приборе Лермантова

Цель работы: Определить модуль Юнга проволоки из растяжения на приборе Лермантова.

Оборудование и принадлежности: прибор Лермантова, индикатор часового типа, штангенциркуль, линейка.

Методика и техника эксперимента

При различных механических воздействиях, вызывающих упругую деформацию образца, справедлив закон Гука, устанавливающий пропорциональность между мерой относительной деформации и напряжением. Напряжением называют отношение деформирующей силы к площади сечения тела:

.

Напряжение называют нормальным, если сила направлена нормально к площади сечения, и касательным (тангенциальным), если сила направлена по касательной к сечению.

В лабораторной работе рассматривается продольное растяжение проволоки. Если растягивать проволоку длиной l и сечением S, закрепив её верхний конец, а к нижнему прикладывать нормальную силу , то она удлинится на.

Согласно закону Гука для деформации растяжения относительное удлинение пропорционально приложенному напряжению, т.е.

, (1)

где Е - модуль упругости (Юнга), зависящий от материала проволоки.

Выразим из (1) модуль Юнга:

. (2)

Модуль Юнга численно равен напряжению, которое привело бы к удлинению образца, равному его первоначальной длине, если для столь большой деформации был бы справедлив закон Гука. Его экспериментальное определение и является задачей данной лабораторной работы. Для этого используется прибор Лермантова.

П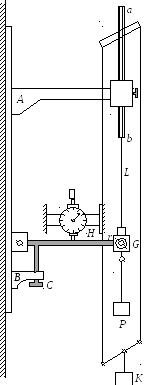рибор Лермантова состоит из двух кронштейновAиB, расположенных один над другим и служащих для укрепления проволоки из исследуемого материала. Нижний кронштейнBснабжен арретиромС. Ввертывая винт С, можно освободить проволоку от нагрузки. Во втулке верхнего кронштейнаАукреплен стерженьab, в отверстии которого зажат верхний конец испытуемой проволокиLдлинойl.

Нижний конец этой проволоки укреплен в отверстии цилиндра G, который опирается на площадку r. Площадка связана с измерительным стержнем H индикатора часового типа , который позволяет непосредственно по шкале определить абсолютное удлинение проволоки, вызываемое грузами на подвесеP. Грузы, необходимые для нагрузки проволоки, находятся на подвесе K внизу прибора. Подвес K укреплён на верхнем кронштейне A. При снятии нагрузки грузы укладывают на подвес K.

Этим достигается постоянство нагрузки на верхнем кронштейне и тем самым постоянство прогиба последнего. Как уже указывалось, нагрузка проволоки и снятие нагрузки производится при поднятом арретире.

Абсолютное удлинение проволоки определяется по шкале индикатора. Оно равно

, (3)

где n₀ – отсчёт по шкале в отсутствии нагрузки; n – отсчёт по шкале после нагружения.

В формуле (2) ,, гдеD – диаметр проволоки. Теперь расчётная формула (2) для модуля Юнга с учётом равенства (3) будет иметь вид:

(4)

Порядок выполнения работы

1. Измерить линейкой или рулеткой длину проволоки l между зажимами.

2. С помощью микрометра или штангенциркуля однократно измерить диаметр проволоки D.

3. При арретированном приборе поместить все грузы на подвес K. Опустив стержень H, снять отсчёт n₀ по шкале индикатора.

4. Перемещая грузы m_i с подвеса K на подвес P, т.е. нагружая испытуемую проволоку, производить отсчеты n_i.

5. Результаты измерений и погрешности измерительных приборов занести в таблицу.

6. По окончании опыта арретировать прибор и снять грузы.

7. Вычислить производимую нагрузку F_i по формуле F_i=m_ig.

8. Построить график зависимости удлинения 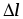от величины нагрузкиF_i. Проверить выполнение закона Гука.

9. Произвести математическую обработку результатов измерений, найти по формуле (4) модуль упругости Е для максимальной нагрузки и его погрешность .

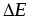Таблица измерений

l, мм	l, мм	D, мм	D, мм	n0, мм	mi, кг	ni, мм	n, мм	мм	, Н