4. Нормирование точности

4.1. Нормирование точности угловых размеров.

Стандарты и допуски угловых размеров

и конических соединений. Конусность уклон

4.1.1. Система единиц на угловые размеры

Углом в плоскости называется геометрическая фигура, образо­ванная двумя лучами (сторонами угла), выходящими из одной точки (вершины).

Двугранным углом называется геометрическая фигура в прост­ранстве, образованная двумя полуплоскостями, исходящими из одной прямой, а также часть пространства, ограниченная этими полуплоско­стями. Полуплоскости называются гранями двугранного угла, а их общая прямая—ребром.

В промышленности чаще всего приходится иметь дело с двугран­ными углами, однако для удобства измерений требования к точности относятся к углу в плоскости, т.е. углу, получаемому пересечением двугранного угла плоскостью, перпендикулярной ребру.

Особую группу наиболее распространенной угловой детали в ма­шиностроении составляют конусы. Используются только круговые конусы, т.е. детали, которые представляют собой поверхность вращения, образованную прямой, вращающейся относительно оси и пересекающей ее. В промышленности используются усеченные конусы, т.е. такие, которые пересечены плоскостью, параллельной основанию (окружности).

За единицу измерения плоского угла в международной системе единиц (СИ) принят радиан.

Радианом называется угол между двумя радиусами (сторонами угла), вырезающий на окружности дугу, длина которой равна радиусу 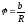, гдеb—длина дуги, R— радиус окружности.

Однако более удобной для измерений является система единиц, основанная на градусной мере, в которой для отсчета угла использу­ются градус, минута и секунда. Особенность этой системы заключается в использовании шестидесятичной системы счисления, т.е. более крупные единицы содержат 60 значений более мелкой (сопоставьте десятичное счисление линейных размеров в метрической системе: 1 м = 10 дециметрам, 1дециметр = 10 см, 1см = 10 мм).

Градусом (°) называется единица плоского угла, равная 1/360 части окружности или 1 /90 части прямого угла. Градус равен 60 угло­вым минутам ( '), а минута—60 угловым секундам ( ").

Соотношения между градусом и радианом:

360 ° = 2π = 6.28318530 рад.; 1 ° = 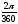= 0.01745329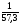рад.;

1 рад. = 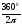= 57°17' 45" = 3437'45" = 206265".

Для оценки малых углов их иногда выражают через тригоно­метрические функции синуса и тангенса, принимая значение этих отношении практически равной значению угла, выраженной в радианной мере, т.е. tg α ≈ α рад.; sin α ≈ α рад.1 Погрешность при такой замене зависит от значения угла (рис. 34).

В машиностроении для удобства измерения отклонение угла от заданного выражают в линейной мере, как изменение размера на определенной длине. Так, для указания точности угла наклона (рис. 35) нормируются допусковые значения h (в мкм) на длине L. Для пересчета линейных и угловых значений целесообразно запомнить, что на длине 206.3 мм (можно принять 200 мм) значение h, равное 1 мкм, соответствует углу в 1".

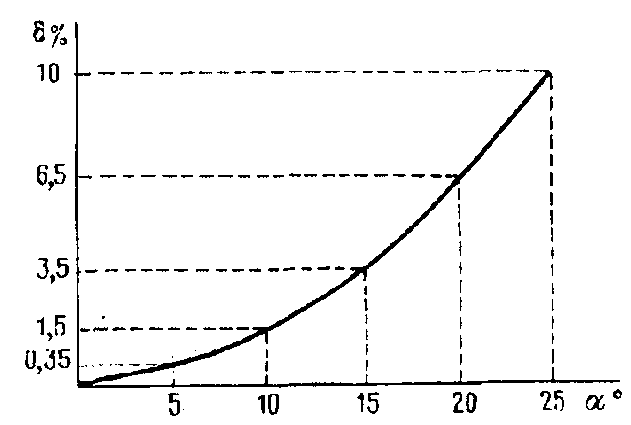
Рис. 34. Погрешность при замене тригоно­метрической функции на значение

Рис. 35. Пересчет угловых величин в линейные

Ссоответствующий пересчет производится при других длинах и высотах с учетом указанного соотношения.

Таким образом, в машиностроении значение угла выражают либо в радианах, либо в градусах, приращении размера в линейной мере на определенной длине, т.е. возможно использовать три единицы для нормирования точности угловых размеров.