Замечания руководителя Содержание

1. Введение............................................................................................................1

1.1. Актуальность работы. 5

1.2. Задание 5

2. Основное содержание работы. 7

2.1. Исследование функции полезности Error: Reference source not found

2.2. Исследование функции ущерба 15

3. Заключение. 19

4. Литература.....................................................................................................21

1. Введение.

1.1 Актуальность работы.

Известно, что с начала момента создания распределённой информационной системы (РИС) существуют риски, которые могут привести к тому, что данная система может частично или полностью выйти из строя. Исключить риски полностью невозможно, но можно продлить жизнеспособность системы, уменьшив их тем или иным образом.

При нанесении ущерба информационной системе возможны два исхода:

1) смерть системы

2) отказ системы с последующим ее восстановлением.

Стоит отметить, что выгода будет потеряна как в первом, так и во втором случае.

В данной работе риск-анализ системы будет проводиться учитывая второй случай, что наиболее часто соответствует реальности. Именно поэтому в работе будет проведено исследование полезности и ущерба РИС.

1.2 Цели и задачи работы:

1. Исследовать функцию полезности и при различных параметрах построить её графики в программе Mathcad .

2. Найти функцию ущерба (как упущенной выгоды) для заданного выражения полезности компонента РИС.

3. Исследовать функцию ущерба и при различных параметрах построить её графики в программе Mathcad.

4. Построить приближение функции полезности.

5. Оценить погрешность приближения.

6. Выяснить вид функции полезности.

7. Сделать вывод по проведенным исследованиям.

2. Основное содержание работы.

2.1. Исследование функции полезности

Цель данной работы состоит в исследовании функции полезности следующего вида:

, где >1 - коэффициент нелинейности, задающий крутизну «заката» функции полезности, - средняя продолжительность работоспособности объекта.

Проведем исследование данной функции полезности:

1. Найдем область определения функции: (в общем случае), так как время не может быть отрицательным. Конкретно в нашем случае время жизни системы определяется параметромT, т.е. система будет существовать ровно времени и поэтому область определения данной функциизначительно уменьшится и станет;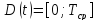

2.Укажем вид функции: – функция общего вида;

3. Исследуем функцию на монотонность. Найдем первую производную функции 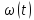и точки экстремума:

=

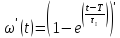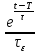
Отсюда получаем, что при любых t производная функции не обращается в ноль, более того, производная всегда меньше нуля(функция убывает). Построив в с помощью mathcad график , получаем:

, где f(t)=

рис.1- исследование функции на монотонность.

4. Исследуем функцию на выпуклость и вогнутость. Для этого сначала найдем вторую производную функции :

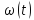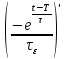= == Отсюда получаем, что при любых t не обращается в ноль, более того, производная всегда меньше нуля( функция является выпуклой на всём интервале).

Построив в с помощью mathcad график , получаем:

где f(t)=

рис.2- исследование функции полезности на выпуклость, вогнутость.

5. Наклонных асимптот нет, так как

Теперь на основание выше проведенного исследования построим график данной функции

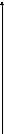
1

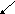
0 T t

Данный график полностью соответствует графику, построенному в программе Mathcad 14.0 при (Рис. 6).

рис.3- График функции в программеMathcad 14.0.

Разложим функцию в ряд Тейлора:

В нашем случае мы ограничимся разложением функции до 2-ого порядком. И чтобы упростить счет, мы положим 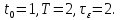Подставив эти выражения в формулу, написанную выше, мы получим следующие:

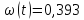-0,303 (t-1) -0,071

Таким образом, наша функция полезности ведёт себя так же, как многочлен 2-ой степени.

Построим первое приближение функции полезности. Она будет иметь следующий вид (Рис. 4).

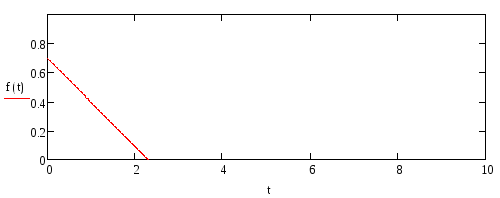
рис.4- первое приближение функции полезности

Теперь построим график второго приближения функции полезности. Он примет следующий вид (Рис. 5).

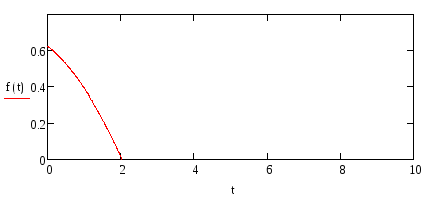
рис.5- второе приближение функции полезности

Таким образом, можно сказать, что практическое и теоретическое построение график совпали.

Построим второе приближение функции ущерба и саму функции ущерба в одной системе координат и при одних и тех же параметрах. И оценим погрешность второго приближения по графику (Рис. 7).

рис.6- оценка погрешности.

,где f(t)- график функции полезности, g(t)- график функции второго приближения.

Видим, что графики накладываются друг на друга. Это означает, что исходную функцию полезности можно заменить функцией для второго приближения.

Итак, построив график данной функции, можно убедиться, что данная функция полезности описывает момент начала атаки на систему с последующим её выходом из строя в момент Т.

Теперь построим серию графиков функции полезности и выясним, при каких значениях параметра 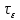площадь, расположенная под графиком, функции будет наибольшей.

Следующие 3 графика были построены в программе Mathcad 14.0 при различных параметрах (во всех графикахT).

рис.8- построения графика при 1

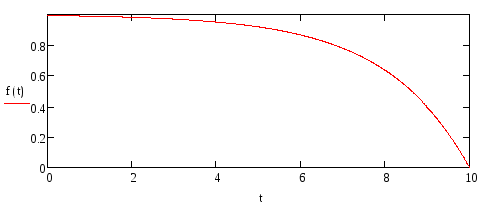
рис.9- построения графика при 2

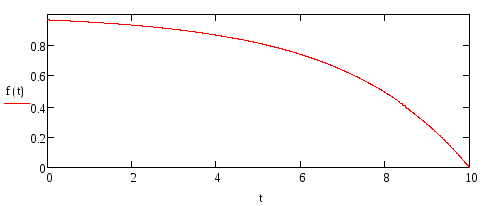
рис.10- построения графика при 3

Следующие 3 графика были построены в программе Mathcad 14.0 при различных параметрах Т (во всех графиках ).

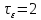рис.11- построения графика при 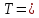2

рис.12- построения графика при 5

рис.13- построения графика при 8

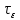
Таким образом, мы видим, что функция приобретает форму прямоугольника при 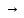1,T

Площадь фигуры под графиком представляет собой упущенную пользу, которую могла бы получить система, если бы в момент времени t=0 атакуемый компонент не утратил безвозвратно свою работоспособность.

Из выше сказанного можно сделать вывод, что при устремление параметра 1, можно извлечь максимальную пользу, т. е. можно заставить функционировать систему на полную мощность с начала её работы и можно уменьшить время выхода её из строя.

Найдем теперь функцию ущерба.

Для того чтобы найти функцию ущерба нужно проинтегрировать функцию полезности 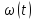в пределах отдо.

= = - +

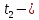
Если в момент времени на систему была совершенна фатальная атака, т. е. система потеряла свою работоспособность, тогдаи ущерб принимает следующий вид:

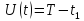
Если же в момент времени на систему была совершенна атака, после которой система продолжает функционировать, тогдаи ущерб будет функцией зависящей от времени, и он принимает следующий вид:

- +

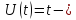
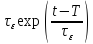Для удобства дальнейших выкладок положим 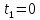, в свою очередь это будет означать, что РИС с момента её начала работы подверглась атаки или вредоносному воздействию и как следствие система несёт ущерб с момента начала её работы.

Тогда аналитическое выражение функции ущерба примет вид:

+
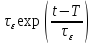