2.2 Исследование функции полезности.

Пусть на определённый сервер компании была проведена хакерская атака, в результате чего сервер вышел из строя и пусть ущерб, которая несёт компания, в результате этой атаки описывается функцией полезности следующего вида:

где и – коэффициенты нелинейности, задающие крутизну «восхода» и «заката» функции полезности, – средняя продолжительность работоспособности объекта

Проведем исследование данной функции полезности:

Для удобства дальнейших выкладок будет целесообразно упростить функцию, т.е. раскрыть скобки и перемножить слагаемые:

1. Найдем область определения функции: (в общем случае), так как время не может быть отрицательным. Конкретно в нашем случае время жизни системы определяется параметром, т.е. система будет существовать ровновремени и поэтому область определения данной функции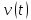значительно уменьшится и станет.

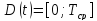2. Укажем вид функции: – функция общего вида;

3. Исследуем функцию на монотонность.

Найдем первую производную функции и точки экстремума:

Отсюда получаем:

или

Из первого сомножителя следует, что

А из второго сомножителя получаем, что

Построим ось координат и отметим на ней точки экстремума (Рис. 10.):

Рис.10. Области возрастания и убывания функции .

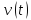Первая точка совпадет с началом координат, а вторая точка разобьёт координатную ось на два промежутка и. Возьмем любую точку из первого промежутка и подставим в. Аналогично возьмем любую точку из второго промежутка и подставим в.

Если получится, что , то это будет означать, что функциявозрастает на данном промежутке, если же получится, что- функцияубывает на данном промежутке.

Так как наша производная задается следующим выражением

то нам не нужно брать какие-либо точки из промежутков и подставлять в функцию. В нашем случае достаточно просто оценить второй сомножитель производной функции, так как знак значения производной функции будет определяться именно этим сомножителем.

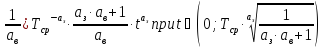
Действительно, так как , а выражениевозрастает медленно прии(по условию).

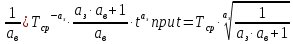
Таким образом, получается, что на промежутке функцияи, следовательно, функциявозрастает на данном промежутке, а на промежуткефункцияи, следовательно, функцияубывает на этом промежутке.

В данном случае точка 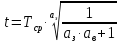является максимумом.

4. Исследуем функцию на выпуклость и вогнутость.

Для этого сначала найдем вторую производную функции .

Отсюда получаем:

или

Из первого сомножителя следует, что

А из второго сомножителя получаем следующее:

где - всегда и– всегда, так как(по условию), следовательно,– не входит в область определения.

Построим ось координат и отметим на ней точки экстремума (Рис. 11.):

Рис. 11. Области выпуклости и вогнутости функции .

Первая точка совпадет с началом координат, а вторая точка не войдет в область определения. Возьмем любую точку из промежутка и подставим в.

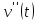Если получится, что , то это будет означать, что функциявогнутая на данном промежутке, если же получится, что- функциявыпуклая на данном промежутке.

В нашем случае получается, что на промежутке функциявогнута.

5. Исследуем функцию на наклонные асимптоты:

где .

Так как , то наклонных асимптот не существует.

6. Найдём кривизну функции.

Посчитаем кривизну функции при :

7. Разложим функцию в ряд Тейлора.

В нашем случае мы ограничимся разложением функции до 2-ого порядком. И чтобы упростить счет мы положим Подставив эти выражения в формулу, написанную выше, мы получим следующие:

Таким образом, наша функция полезности ведёт себя так же, как многочлен 2-ой степени.

Найдём точки, в которых :

Отсюда получаем:

или

Из первого сомножителя следует, что

А из второго сомножителя получаем, что

Теперь на основание выше проведенного исследования построим график данной функции (Рис. 12.).

Рис. 12. График функции .

где – экстремум функции соответствующий максимуму.

Данный график полностью соответствует графику, построенному в программе Mathcad 14.0 при (Рис. 13.).

Рис. 13. График функции в программеMathcad 14.0.

Таким образом, можно сказать, что практическое и теоретическое построение график совпали.

Найдем теперь функцию ущерба.

Для того чтобы найти функцию ущерба нужно проинтегрировать функцию полезности в пределах отдо. Где– момент времени атаки или вредоносного воздействия на распределенную информационную систему, а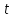– переменная по времени.

Для удобства дальнейших выкладок положим , в свою очередь это будет означать, что РИС с момента её начала работы подверглась атаки или вредоносному воздействию и как следствие система несёт ущерб с момента начала её работы.

Тогда аналитическое выражение ущерба примет вид: