
- •Общие рекомендации студенту-заочнику к изучению курса “численные методы”
- •Правила выполнения и оформления контрольной работы
- •Программа курса “численные методы” для студентов –-заочников инженерно-технических специальностей (четвертый семестр)
- •Контрольная работа Задача №1 интерполирование функций с помощью многочлена ньютона
- •Задача №2 метод наименьших квадратов
- •Задача №3
- •Задача №2
- •Задача №3
- •Задача №4
- •Решение. Пусть дано уравнение с одним неизвестным вида
- •Задача №5
- •Задача №6
- •Задача №7
- •Библиографический список
- •Содержание
Задача №3
ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Задание.Получить приближенное решение системы методом простой итерации с точностью 0.01.
№1.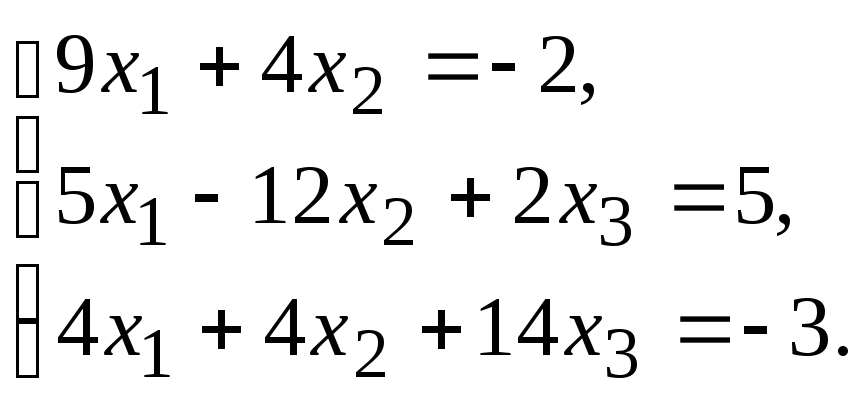 №2.
№2.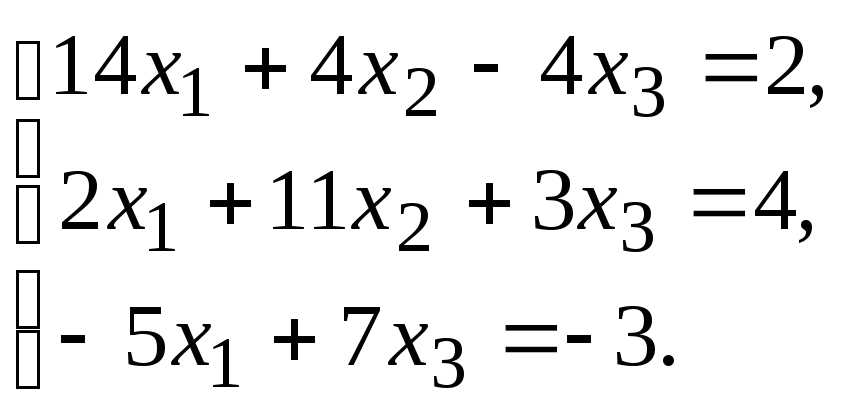
№3.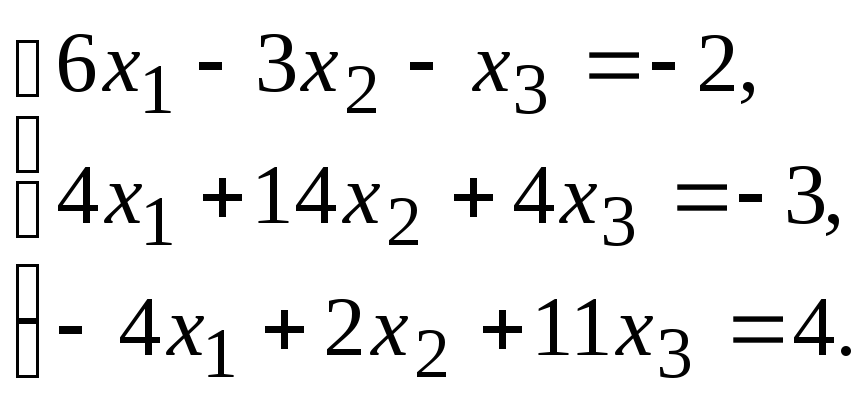 №4.
№4.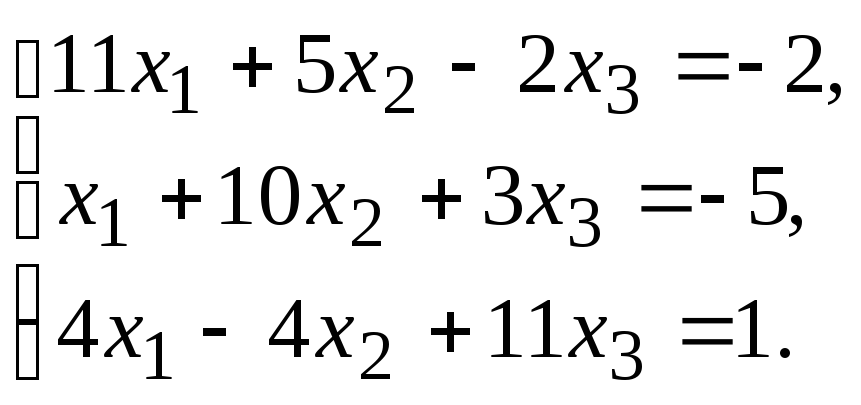
№5.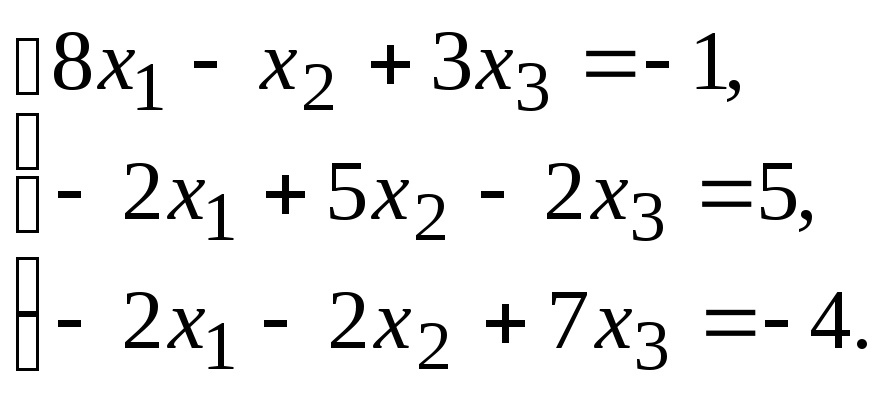 №6.
№6.
№7.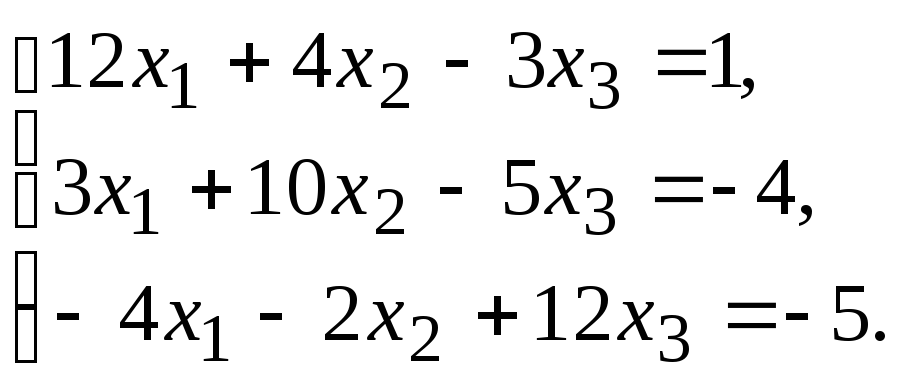 №8.
№8.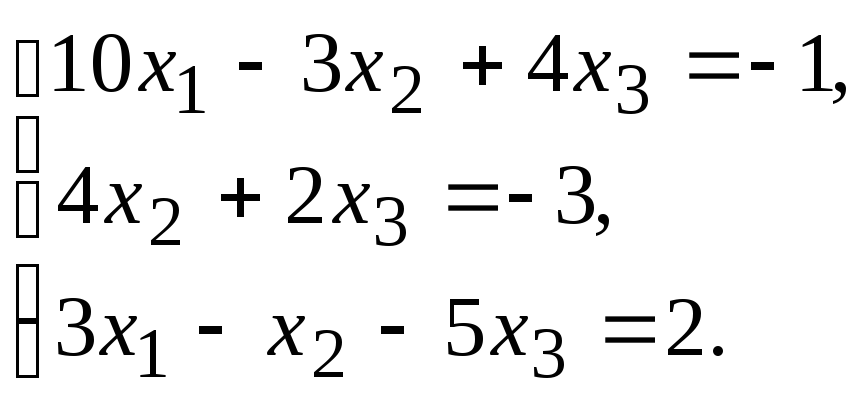
№9.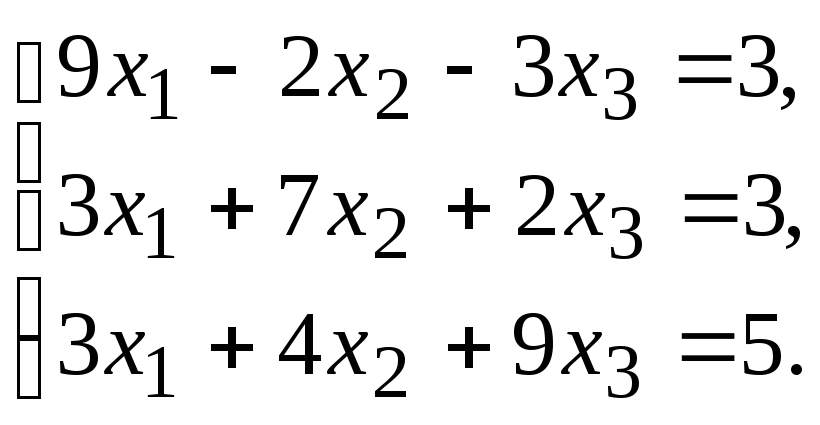 №10.
№10.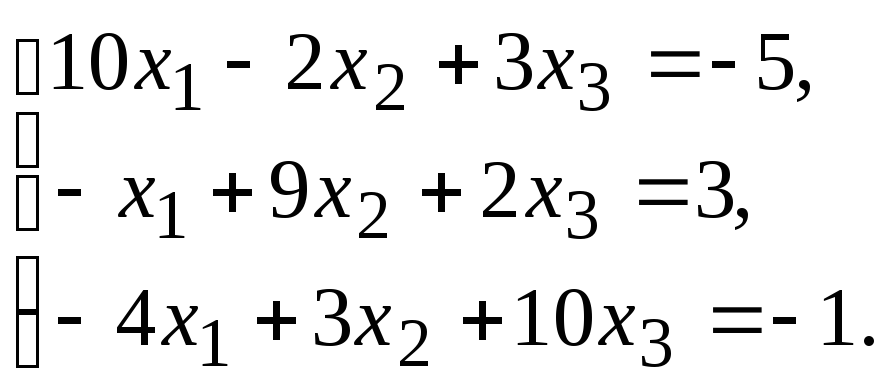
№11.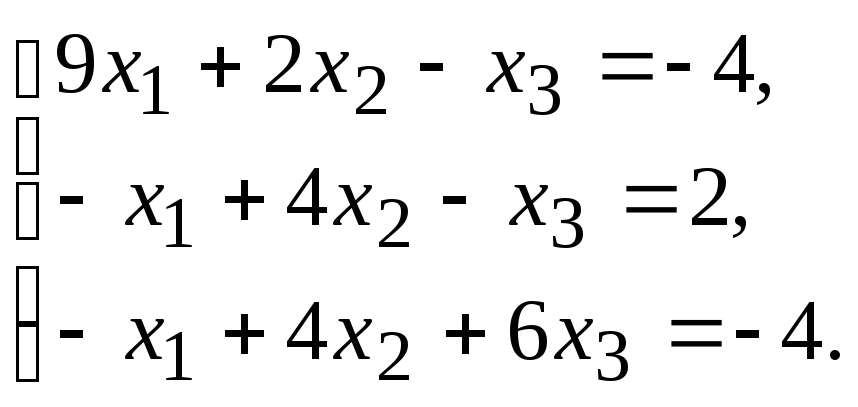 №12.
№12.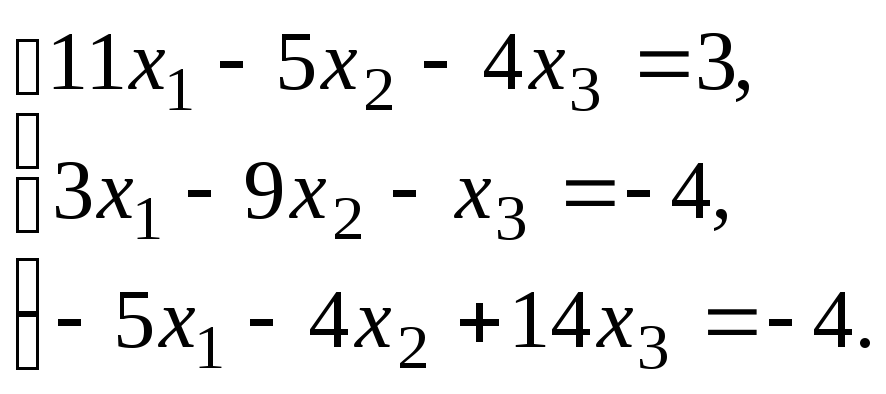
№13.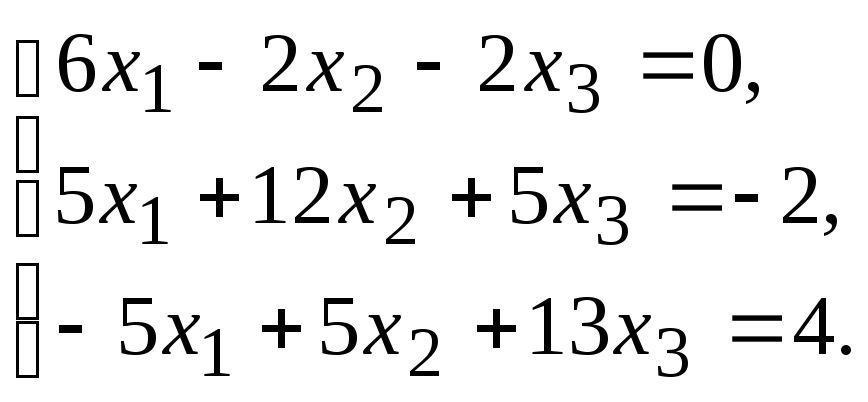 №14.
№14.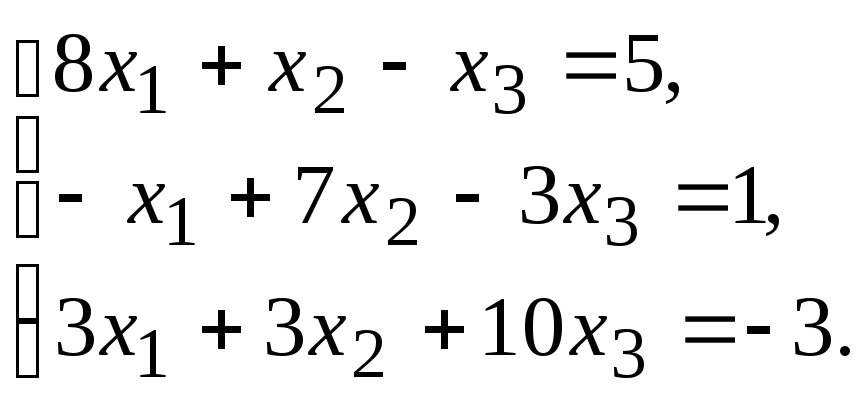
№15.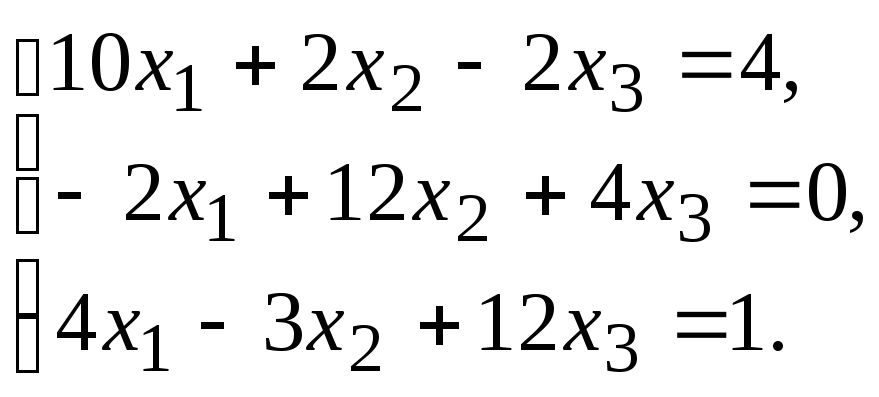 №16.
№16.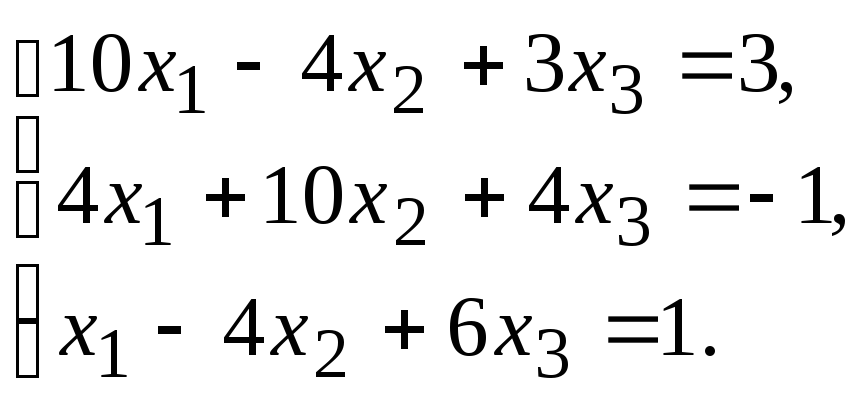
№17.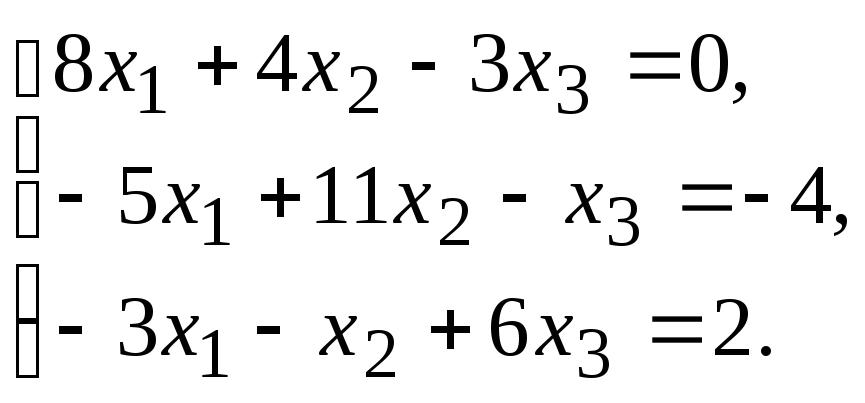 №18.
№18.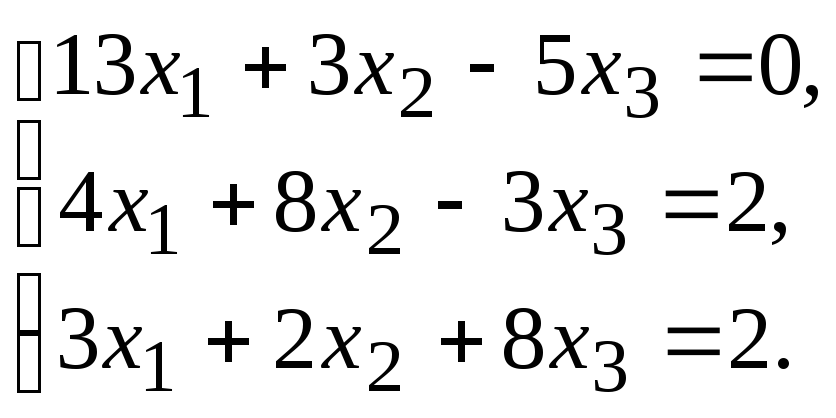
№19.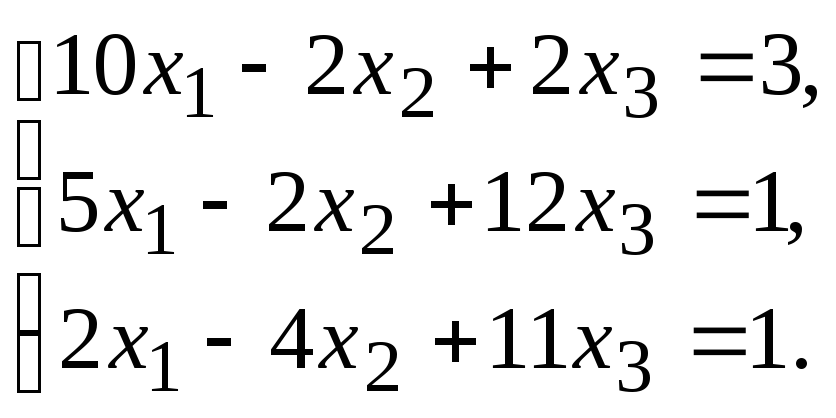 №20.
№20.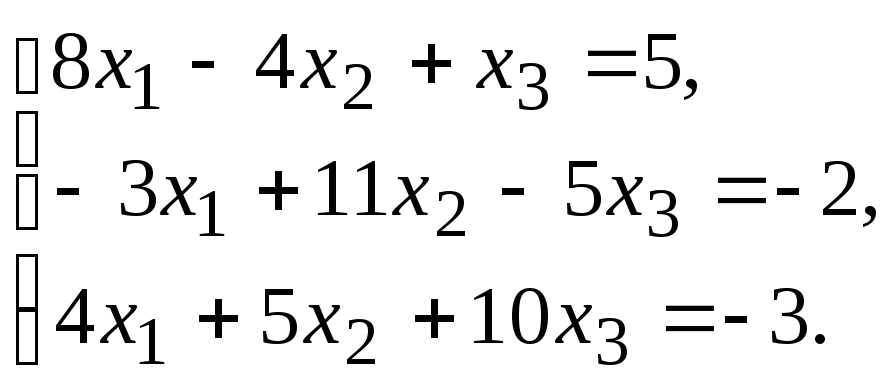
Задача №4
ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Задание. Отделить корни и найти приближенное решение заданного уравнения с точностью 0.01 методом Ньютона (вариант 1-10) и методом итераций (вариант 11-20).
№1.![]() №2.
№2.![]()
№3.![]() №4.
№4.![]()
№5.![]() №6.
№6.![]()
№7.![]() №8.
№8.
![]()
№9.![]() №10.
№10.![]()
№11.![]() №12.
№12.![]()
№13.![]() №14.
№14.![]()
№15.![]() №16.
№16. ![]()
№17.![]() №18.
№18.![]()
№19.![]() №20.
№20.![]()
Задача №5
ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
Задание. 1) Вычислить интеграл по формуле трапеций с тремя десятичными знаками после запятой.
2)
Вычислить
интеграл по формуле Симпсона при
![]() .
оценить погрешность результата, составив
таблицу конечных разностей.
.
оценить погрешность результата, составив
таблицу конечных разностей.
№1.![]() №2.
№2.![]()
№3.![]() №4.
№4.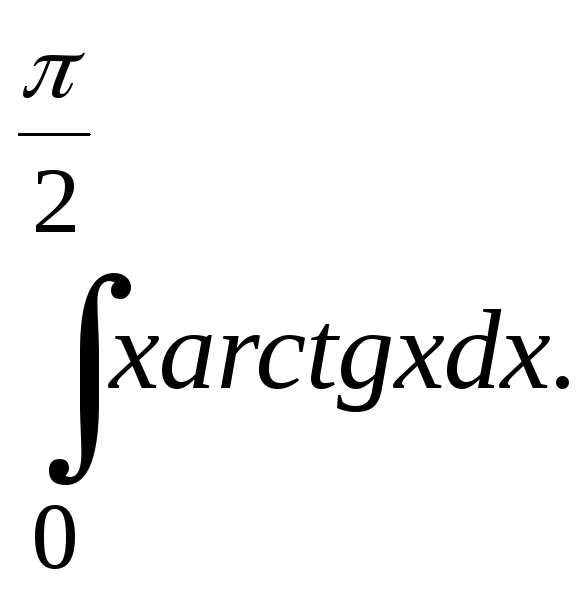
№5.![]() №6.
№6.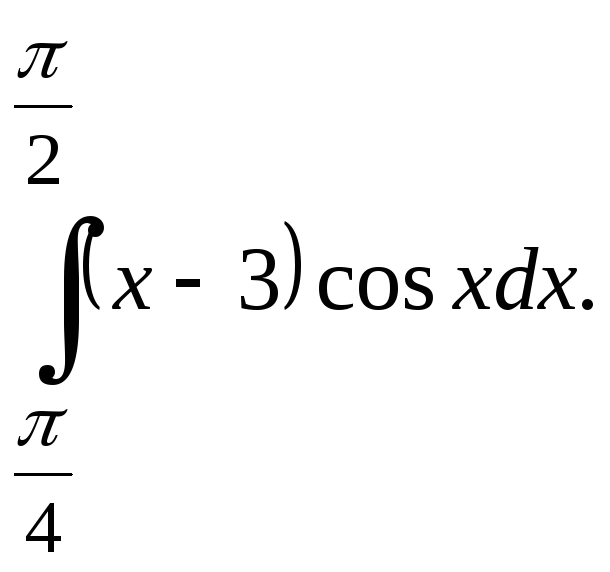
№7.![]() №8.
№8.![]()
№9.![]() №10.
№10.![]()
№11.![]() №12.
№12.![]()
№13.![]() №14.
№14.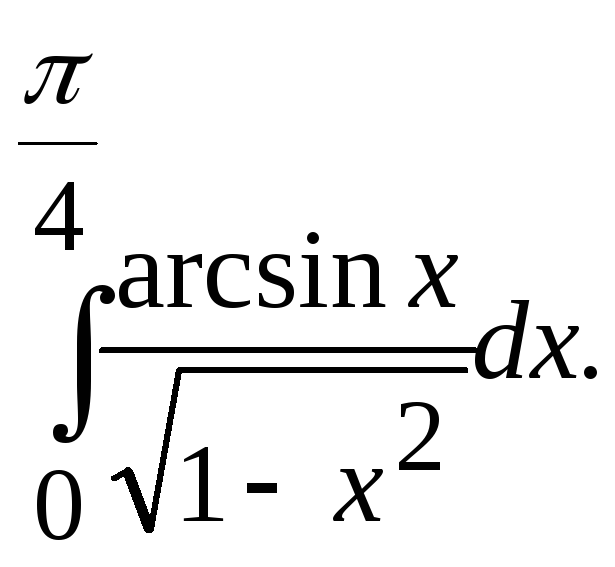
№15.![]() .№16.
.№16.![]() .
.
№17.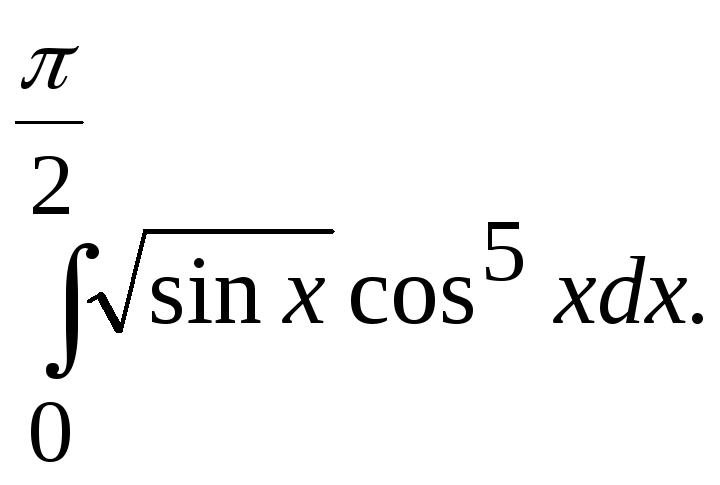 №18.
№18.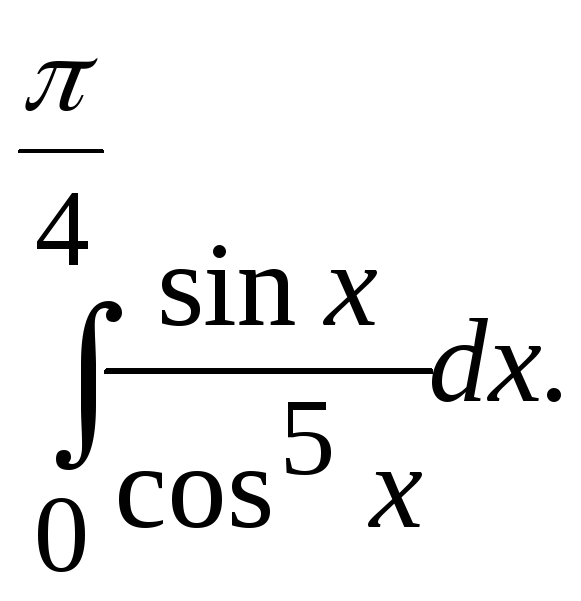
№19.![]() №20.
№20.![]()
Задача №6
ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ.
ЗАДАЧА КОШИ
Задание.
Получить численное решение
дифференциального уравнения![]() ,
удовлетворяющее заданному начальному
условию
,
удовлетворяющее заданному начальному
условию![]() на отрезке
на отрезке![]() cшагом
cшагом![]() ,
методом Эйлера.
,
методом Эйлера.
№1.![]() .
.
№2.![]() .
.
№3.![]() .
.
№4.![]() .
.
№5.![]() .
.
№6.![]() .
.
№7. ![]() .
.
№8.![]() .
.
№9.![]() .
.
№10.![]() .
.
№11.![]() .
.
№12.![]() .
.
№13.![]() .
.
№14.![]() .
.
№15.![]() .
.
№16.![]() .
.
№17.![]() .
.
№18.![]() .
.
№19.![]() .
.
№20.![]() .
.
Задача №7
РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Задание. Найти численное решение линейной краевой задачи
для
дифференциального уравнения второго
порядка конечно-разностным методом,
используя аппроксимацию производных
второго порядка и шаг
![]() .
.
№1.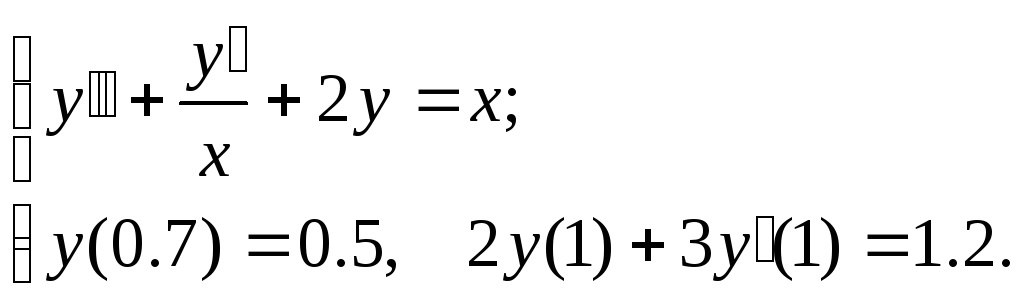
№2.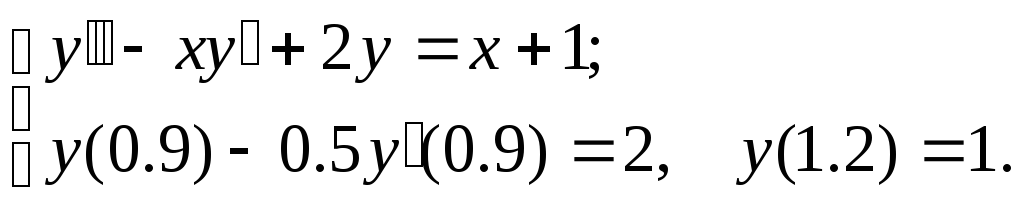
№3.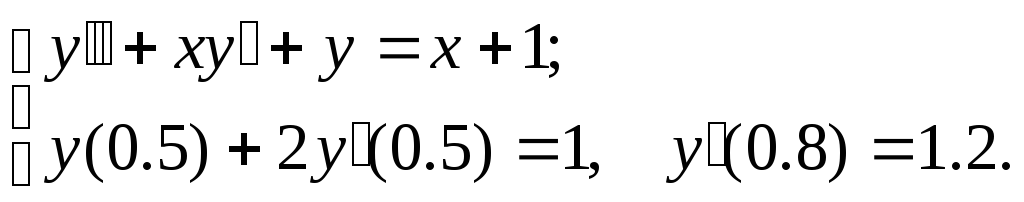
№4.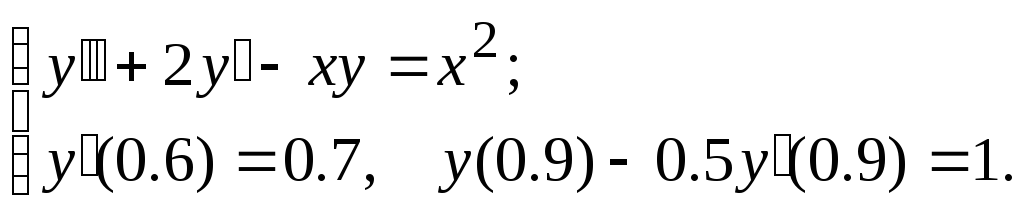
№5.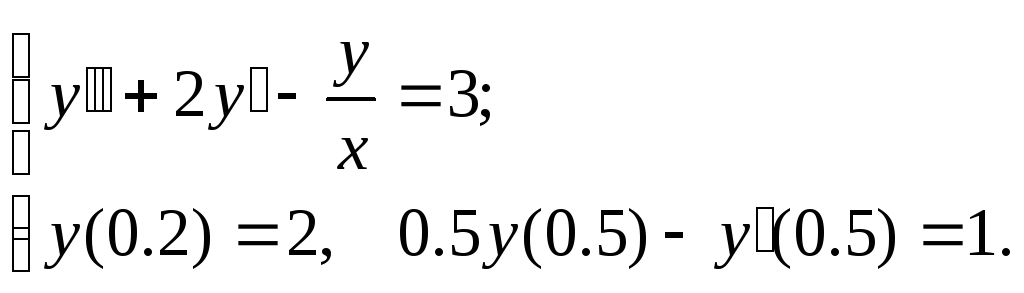
№6.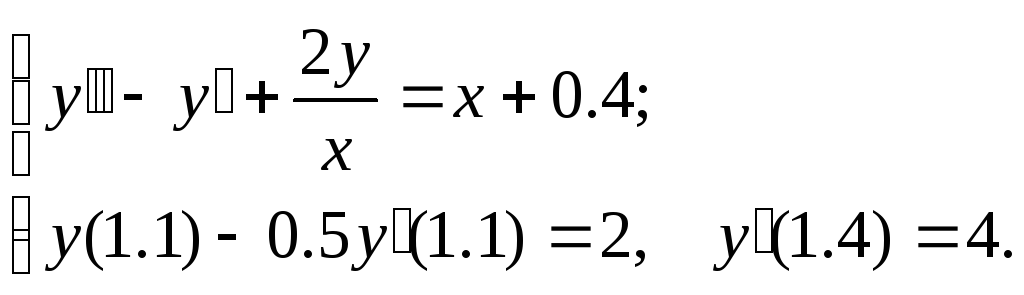
№7. 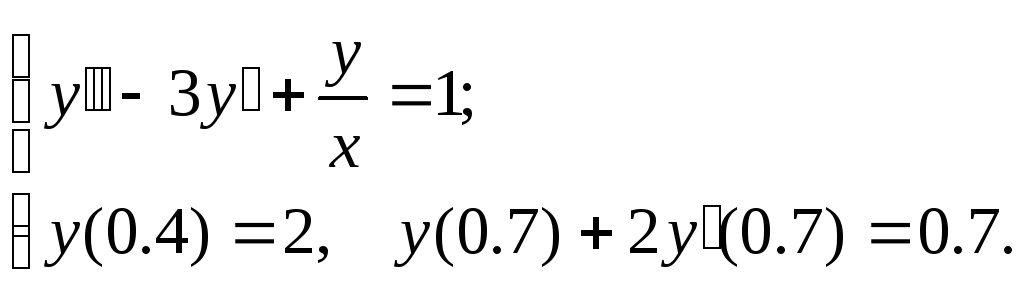
№8.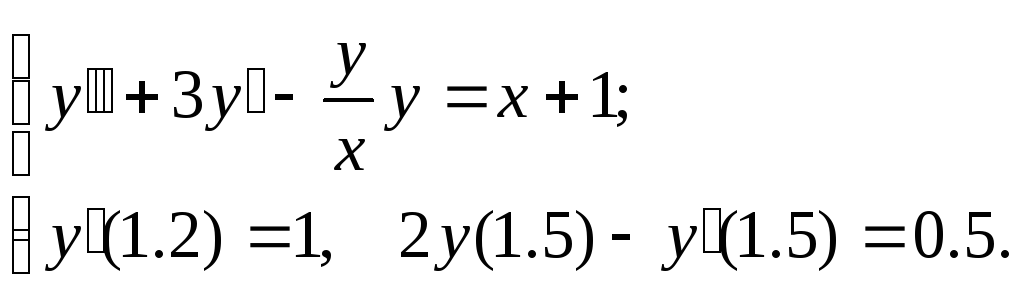
№9.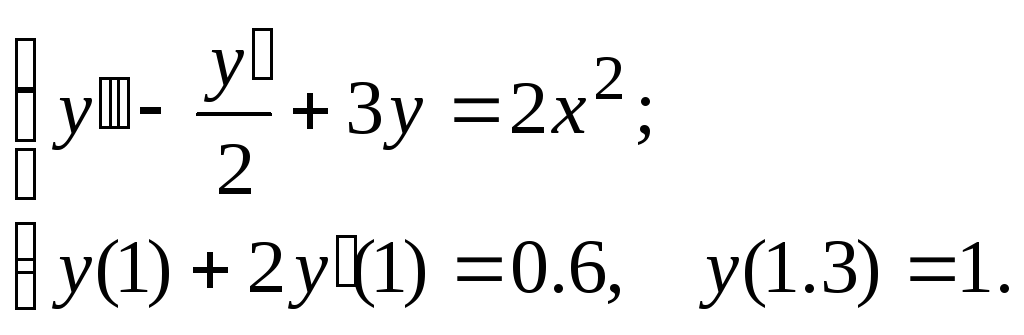
№10.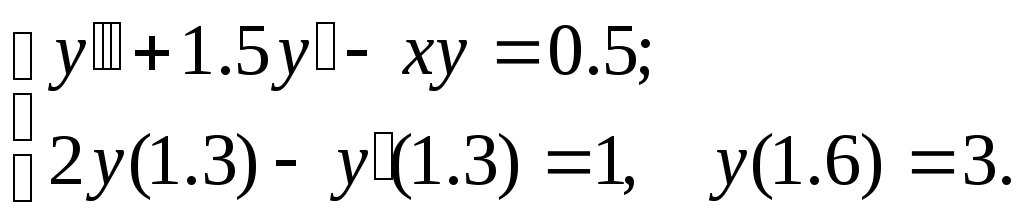
№11.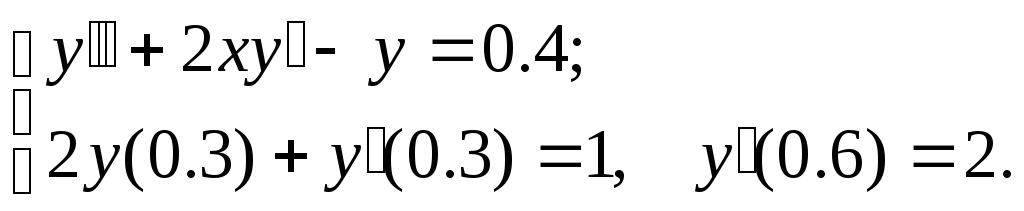
№12.
№13.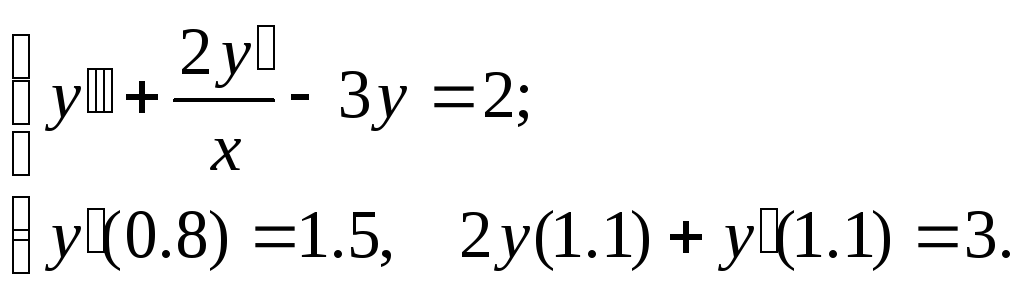
№14.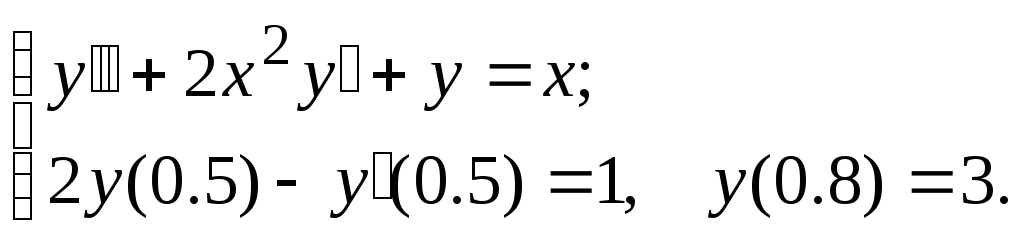
№15.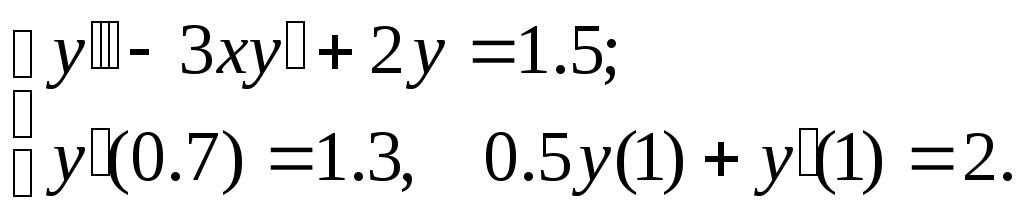
№16.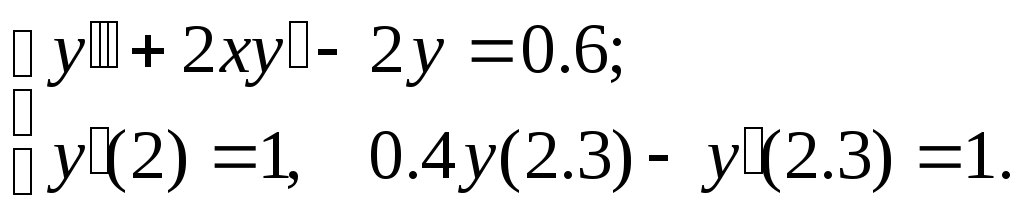
№17.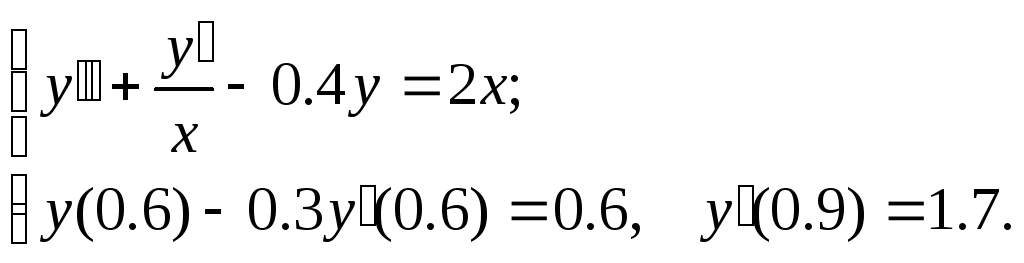
№18.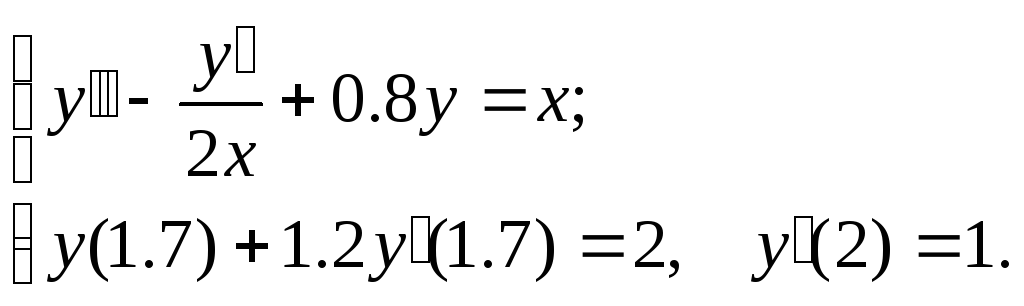
№19.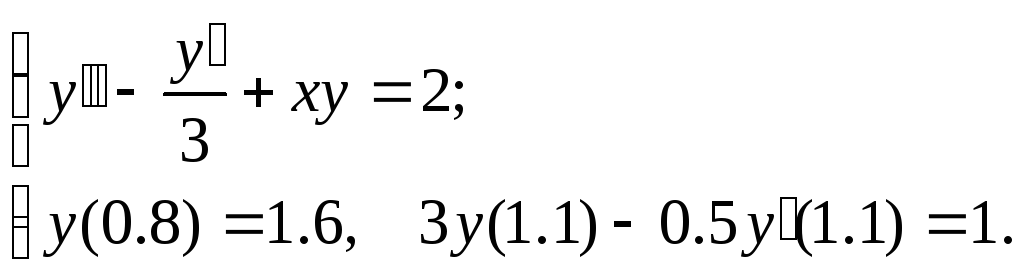
№20.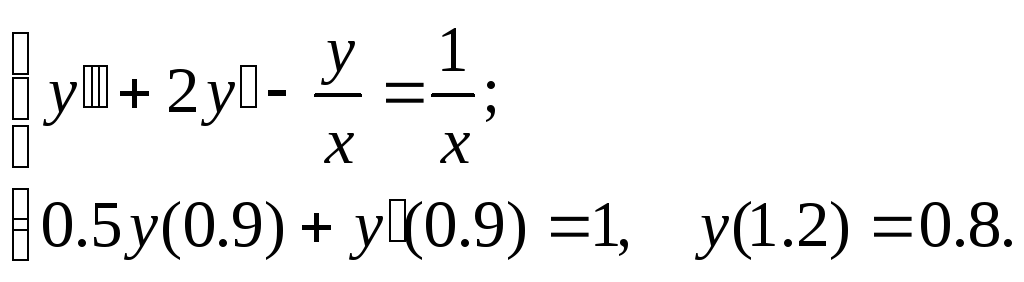
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ К КОНТРОЛЬНОЙ РАБОТЕ
Задача №1
Дана таблица
значений функции
![]() .
Построить для этой функции интерполяционный
многочлен Ньютона и с помощью его найти
приближенное значение функции для
заданного аргумента
.
Построить для этой функции интерполяционный
многочлен Ньютона и с помощью его найти
приближенное значение функции для
заданного аргумента
![]() .
.
|
X |
3.50 |
3.55 |
3.60 |
3.65 |
3,70 |
|
|
Y |
33.115 |
34.813 |
36.598 |
38.475 |
40.447 |
3.57 |
Решение.
Часто приходится рассматривать
функции![]() ,
заданные табличными значениями
,
заданные табличными значениями![]() .
Эти значения могут быть получены в
результате расчета, эксперимента, опыта
и т.д. Значения же функции в промежуточных
точках неизвестны и их получение может
быть связано с проведением сложных
расчетов и экспериментов. В некоторых
случаях даже при известной зависимости
.
Эти значения могут быть получены в
результате расчета, эксперимента, опыта
и т.д. Значения же функции в промежуточных
точках неизвестны и их получение может
быть связано с проведением сложных
расчетов и экспериментов. В некоторых
случаях даже при известной зависимости
![]() ее использование в практических расчетах
затруднительно из-за ее громоздкости
(содержит трудно вычисляемые выражения,
сложные интегралы и т.д.).
ее использование в практических расчетах
затруднительно из-за ее громоздкости
(содержит трудно вычисляемые выражения,
сложные интегралы и т.д.).
В связи с этим
возникает задача о приближении
(аппроксимации) функций: функцию
![]() ,
заданную таблично или аналитически,
аппроксимировать функцией
,
заданную таблично или аналитически,
аппроксимировать функцией![]() так, чтобы отклонение
так, чтобы отклонение![]() от
от![]() в заданной области было наименьшим.
Функция
в заданной области было наименьшим.
Функция![]() при этом называется аппроксимирующей.
при этом называется аппроксимирующей.
На практике очень важен случай аппроксимации функции многочленом
![]() .
(1)
.
(1)
При этом коэффициенты
![]() подбираются так, чтобы достичь наименьшего
отклонения многочлена от данной функции.
В этом случае будем говорить о
полиномиальной аппроксимации или
кусочно-полиномиальной аппроксимации.
подбираются так, чтобы достичь наименьшего
отклонения многочлена от данной функции.
В этом случае будем говорить о
полиномиальной аппроксимации или
кусочно-полиномиальной аппроксимации.
Если приближение
строится на заданном дискретном
множестве точек
![]() ,
то аппроксимация называется точечной.
К ней относятся интерполирование,
среднеквадратичное приближение и
другие.
,
то аппроксимация называется точечной.
К ней относятся интерполирование,
среднеквадратичное приближение и
другие.
При
построении приближения на непрерывном
множестве точек (например, на отрезке
![]() ),
аппроксимация называется непрерывной
(или интегральной).
),
аппроксимация называется непрерывной
(или интегральной).
Одним из основных
типов точечной аппроксимации является
интерполирование. Оно состоит в
следующем: для данной функции
![]() строим многочлен (1), принимающий в
заданных точках
строим многочлен (1), принимающий в
заданных точках![]() те же значения
те же значения![]() ,
что и функция
,
что и функция![]() ,
т.е.
,
т.е.
![]() ,
,
![]() . (2)
. (2)
При этом
предполагается, что среди значений
![]() нет одинаковых, т.е.
нет одинаковых, т.е.![]() при
при![]() .
.
Точки
![]() называются узлами интерполяции, а
многочлен
называются узлами интерполяции, а
многочлен![]() - интерполяционным многочленом. Близость
интерполяционного многочлена к заданной
функции состоит в том, что их значения
совпадают на заданной системе точек.
- интерполяционным многочленом. Близость
интерполяционного многочлена к заданной
функции состоит в том, что их значения
совпадают на заданной системе точек.
Максимальная
степень интерполяционного многочлена
![]() ,
где
,
где![]() -число
узлов,
-число
узлов,![]() -степень
многочлена. В этом случае говорят о
глобальной интерполяции, так как один
многочлен
-степень
многочлена. В этом случае говорят о
глобальной интерполяции, так как один
многочлен
![]() (3)
(3)
используется
для интерполяции функции
![]() на всем рассматриваемом интервале
аргумента
на всем рассматриваемом интервале
аргумента![]() .
Коэффициенты
.
Коэффициенты![]() многочлена (3) находятся из системы
уравнений (2).
многочлена (3) находятся из системы
уравнений (2).
Построим теперь
интерполяционный многочлен, единый для
всего отрезка
![]() . Пусть для функции
. Пусть для функции![]() заданы
заданы![]() значения таблично заданной функции
значения таблично заданной функции![]() для равноотстоящих значений независимой
переменной:
для равноотстоящих значений независимой
переменной:![]() ,
,![]() ,
где
,
где![]() шаг
интерполяции.
шаг
интерполяции.
-
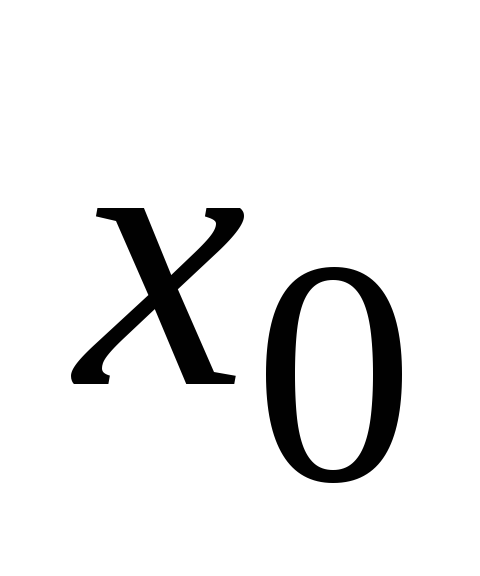
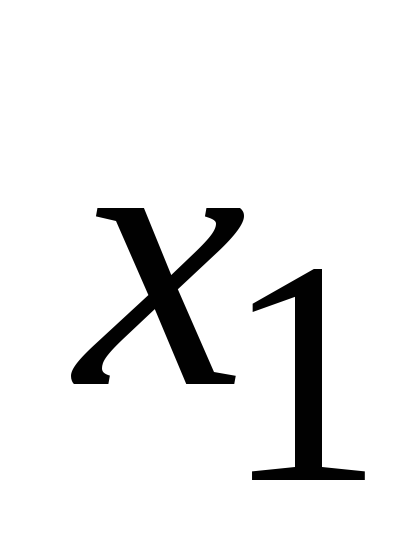
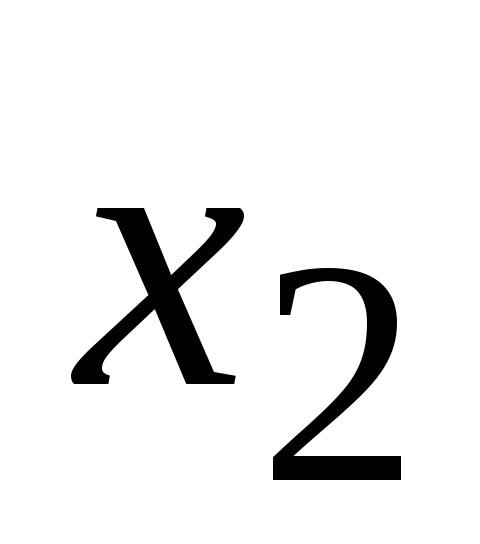
…
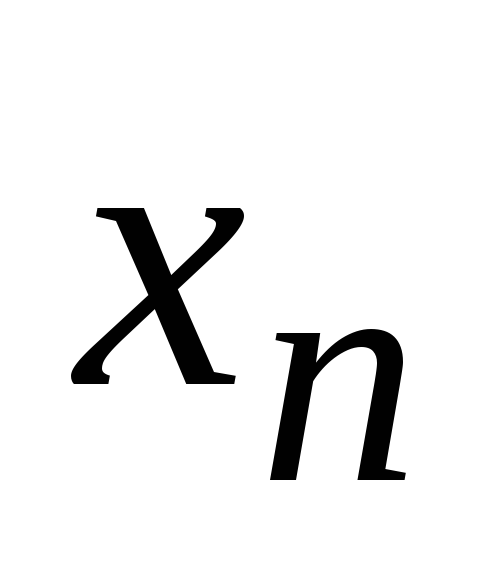

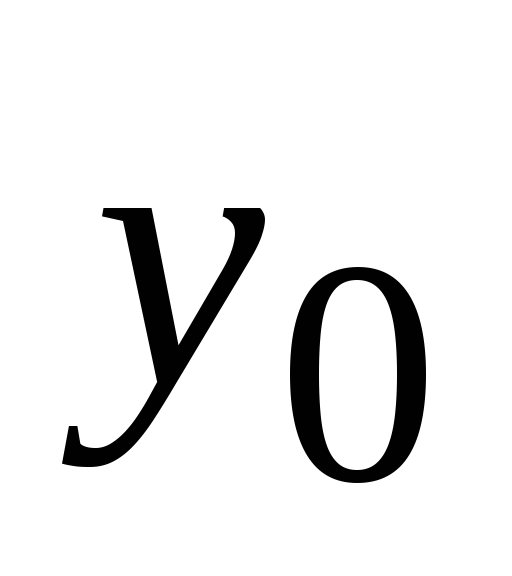
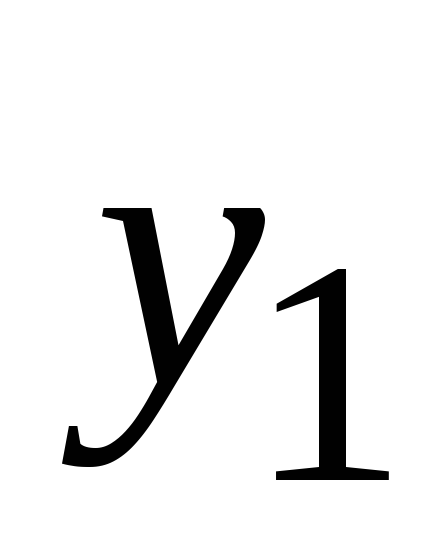
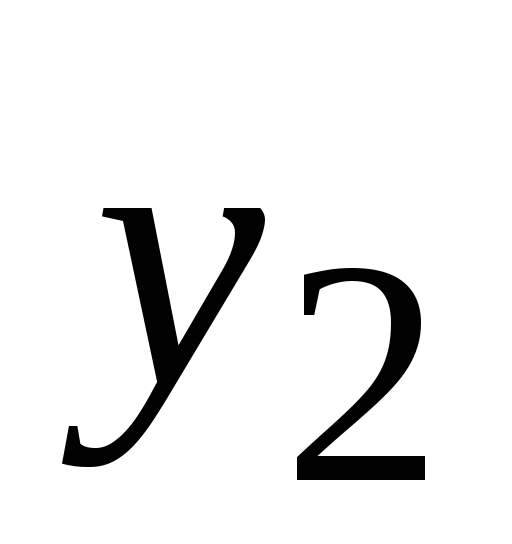
…
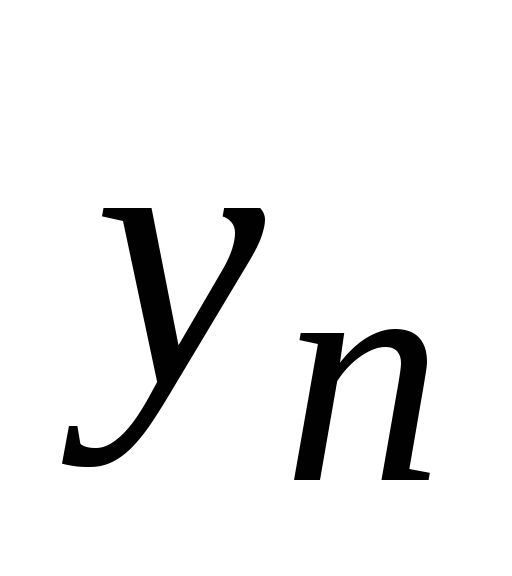
Прежде чем получить такие формулы, рассмотрим элементы конечных разностей.
Составим разности значений заданной функции:
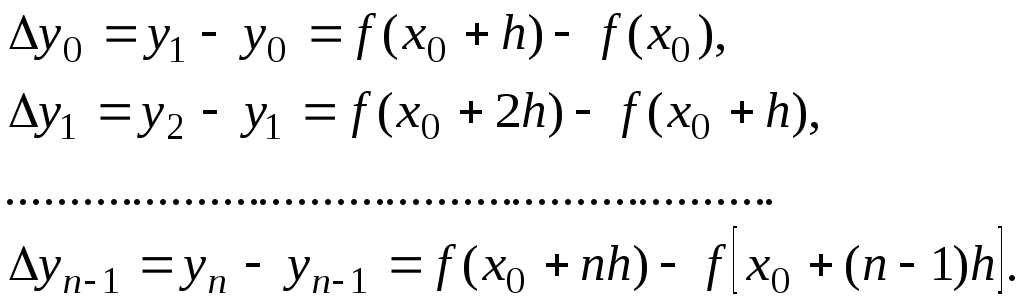
Эти
разности называются конечными разностями
первого порядка функции. Из них, в свою
очередь, таким же образом можно получить
![]() конечных разностей второго порядка,
или вторых разностей:
конечных разностей второго порядка,
или вторых разностей:
![]() Аналогично
определяются разности IIIиIVи т.д. порядков. Разность
порядка
Аналогично
определяются разности IIIиIVи т.д. порядков. Разность
порядка![]() определяется формулой:
определяется формулой:
![]() ,
,
где
![]() и
и![]() .
.
В некоторых случаях требуется знать выражения конечных разностей непосредственно через значения функции. Для нескольких первых порядков разностей их можно получить непосредственной подстановкой
![]() ;
;
![]()
![]()
![]()
Аналогично
для любого
![]() можно записать:
можно записать:
![]() .
.
Такую же формулу
можно записать и для значения разности
в узле
![]() :
:
![]() .
.
Для функции
![]() ,
заданной таблицей своих значений
,
заданной таблицей своих значений![]() в узлах
в узлах![]() ,
конечные разности разных порядков
удобно помещать в одну общую таблицу с
узлами и значениями функции. Обычно
используют горизонтальную таблицу или
диагональную таблицу конечных разностей
,
конечные разности разных порядков
удобно помещать в одну общую таблицу с
узлами и значениями функции. Обычно
используют горизонтальную таблицу или
диагональную таблицу конечных разностей
Интерполяционный многочлен Ньютона для заданной функции имеет вид
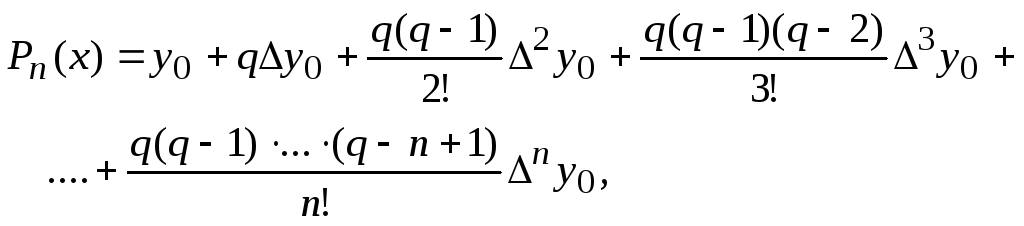 (4)
(4)
где
![]() .
.
Интерполяционную
формулу (4) обычно используют для
вычисления значений функции в левой
половине отрезка. Дело в том, что разности
![]() вычисляются через значения функции
вычисляются через значения функции![]() ,
причем
,
причем
![]() .
Поэтому при больших значениях
.
Поэтому при больших значениях![]() мы не можем вычислить разности высших
порядков
мы не можем вычислить разности высших
порядков![]() .
Например, при
.
Например, при
![]() в (4) можно учесть только
в (4) можно учесть только
![]() ,
,
![]() и
и
![]() .
.
Составим таблицу конечных разностей для заданных значений (таблица 1):
Таблица 1
|
|
|
|
|
|
|
3.50 3.55 3.60 3.65 3.70 |
33.115 34.813 36.598 38.475 40.447 |
1.698 1.785 1.877 1.972 ------ |
0.087 0.092 0.095 ------ ------ |
0.005 0.003 ------ ------ ------ |
При составлении
таблицы конечных разностей ограничиваемся
разностями третьего порядка, так как
они практически постоянны. Поэтому в
формуле Ньютона полагаем
![]() .
Приняв
.
Приняв![]() ,
,![]() ,
будем иметь:
,
будем иметь:
![]()
или
![]()
где
![]()
Подставим
в выражение для
![]() вместо
вместо![]() значение
значение![]() .
.
Получим
![]()
Тогда,
 Следовательно,
Следовательно,![]()
