
- •2. Найти производные заданных функций
- •3. Найти интегралы
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12.
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
Варианты заданий к РГР
Найти указанные пределы
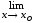
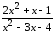


 :
а) х
:
а) х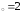 ,
б) х
,
б) х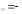 1,
в) х
1,
в) х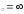 .
.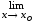
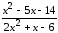


 :
а) х
:
а) х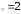 ,
б) х
,
б) х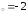 ,
в) х
,
в) х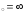 .
.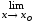
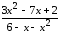

 : а) х
: а) х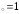 ,
б) х
,
б) х ,
в) х
,
в) х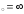 .
.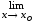
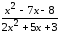 : а) х
: а) х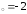 ,
б) х
,
б) х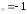 ,
в) х
,
в) х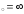 .
.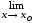
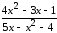 : а) х
: а) х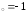 ,
б) х
,
б) х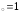 ,
в) х
,
в) х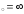 .
.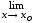
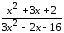 : а) х
: а) х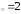 ,
б) х
,
б) х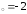 ,
в) х
,
в) х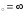 .
.
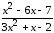 : а) х
: а) х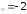 ,
б) х
,
б) х ,
в) х
,
в) х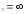 .
.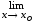
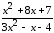 : а) х
: а) х ,
б) х
,
б) х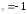 ,
в) х
,
в) х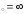 .
.
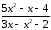 : а) х
: а) х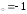 ,
б) х
,
б) х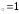 ,
в) х
,
в) х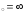 .
.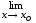
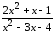 : а) х
: а) х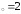 ,
б) х
,
б) х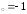 ,
в) х
,
в) х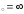 .
.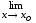
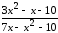 : а) х
: а) х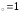 ,
б) х
,
б) х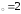 ,
в) х
,
в) х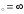 .
.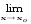
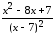 : а) х
: а) х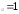 ,
б) х
,
б) х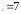 ,
в) х
,
в) х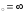 .
.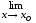
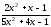 : а) х
: а) х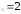 ,
б) х
,
б) х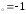 ,
в) х
,
в) х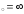 .
.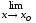
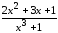 : а) х
: а) х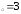 ,
б) х
,
б) х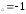 ,
в) х
,
в) х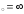 .
.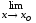
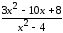 : а) х
: а) х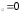 ,
б) х
,
б) х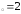 ,
в) х
,
в) х .
.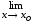
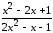 : а) х
: а) х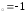 ,
б) х
,
б) х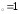 ,
в) х
,
в) х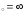 .
.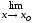
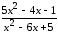 : а) х
: а) х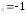 ,
б) х
,
б) х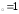 ,
в) х
,
в) х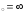 .
.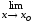
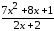 : а) х
: а) х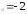 ,
б) х
,
б) х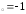 ,
в) х
,
в) х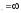 .
.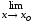
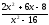 : а) х
: а) х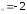 ,
б) х
,
б) х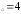 ,
в) х
,
в) х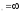 .
.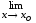
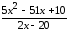 : а) х
: а) х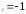 ,
б) х
,
б) х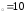 ,
в) х
,
в) х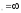 .
.
2. Найти производные заданных функций
а) у=
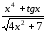 ;
б) у=cos
ln8x;
;
б) у=cos
ln8x;а)у=
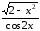 ;
б) у=ln
arcsin3x;
;
б) у=ln
arcsin3x;а) у=
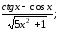 б) у=arctg
ln5x;
б) у=arctg
ln5x;а) у=
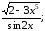 б) у=ln
cos4x;
б) у=ln
cos4x;а) у=
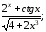 б) у=cos
ln7x;
б) у=cos
ln7x;а) у=
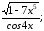 б) у=ln
sin7x;
б) у=ln
sin7x;а) у=
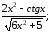 б) у=arctg
ln5x;
б) у=arctg
ln5x;а) у=
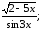 б) у=ln
arcsin2x;
б) у=ln
arcsin2x;а) у=
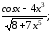 б) у=sin
ln7x;
б) у=sin
ln7x;а) у=
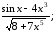 б) у=tg
ln7x;
б) у=tg
ln7x;
а) у=
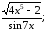 б) у=ln
cos6x;
б) у=ln
cos6x;а) у=
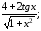 б) у=ln
arctg2x;
б) у=ln
arctg2x;а) у=
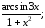 б) у=cos
ln(5x+1);
б) у=cos
ln(5x+1);а) у=
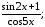 б) у=arccos
ln4x;
б) у=arccos
ln4x;а) у=
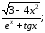 б) у=arctg
ln5x;
б) у=arctg
ln5x;а) у=
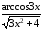 ;
б) у=ln
sin(6x+1);
;
б) у=ln
sin(6x+1);а) у=
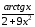 ;
б) у=sin
ln(1-2x);
;
б) у=sin
ln(1-2x);а) у=
 ;
б) у=ln
arccos5x;
;
б) у=ln
arccos5x;а) у=
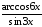 ;
б) у=arcsin
ln(2x-1);
;
б) у=arcsin
ln(2x-1);а) у=
 ;
б) у=ln
arccos7x.
;
б) у=ln
arccos7x.
3. Найти интегралы
Вариант №1

1.
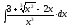 2.
2.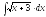 3.
3.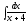
4.
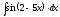 5.
5.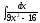 6.
6.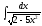
7.
 8.
8.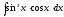
Вариант №2
1.
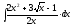 2.
2. 3.
3.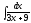
4.
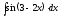 5.
5. 6.
6.
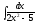
7.
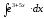 8.
8.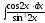
Вариант №3
1.
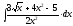 2.
2.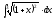 3.
3.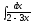
4.
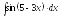 5.
5.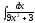 6.
6.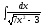
7.
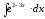 8.
8.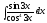
Вариант №4
1.
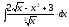 2.
2.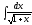 3.
3.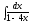
4.
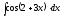 5.
5.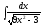 6.
6.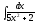
7.
 8.
8.
Вариант №5
1.
 2.
2.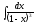 3.
3.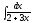
4.
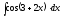 5.
5.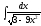 6.
6.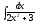
7.
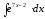 8.
8.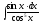
Вариант №6
1.
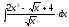 2.
2.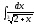 3.
3.
4.
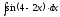 5.
5.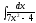 6.
6.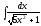
7.
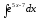 8.
8.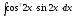
Вариант №7
1.
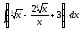 2.
2.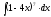 3.
3.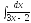
4.
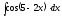 5.
5.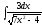 6.
6.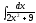
7.
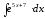 8.
8.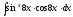
Вариант №8
1.
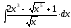 2.
2.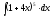 3.
3.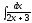
4.
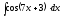 5.
5. 6.
6.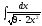
7.
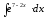 8.
8.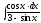
Вариант №9
1.
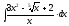 2.
2. 3.
3.
4.
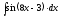 5.
5.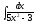 6.
6.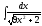
7.
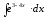 8.
8.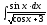
Вариант №10
1.
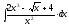 2.
2.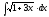 3.
3.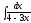
4.
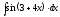 5.
5.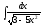 6.
6.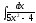
7.
 8.
8.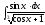
Вариант №11
1.
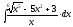 2.
2.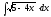 3.
3.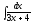
4.
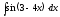 5.
5.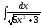 6.
6.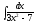
7.
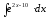 8.
8.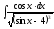
Вариант №12
1.
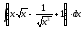 2.
2.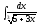 3.
3.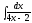
4.
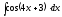 5.
5.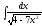 6.
6.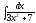
7.
 8.
8.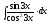
Вариант №13
1.
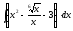 2.
2.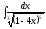 3.
3.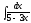
4.
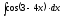 5.
5.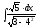 6.
6.
7.
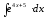 8.
8.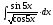
Вариант №14
1.
 2.
2.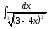 3.
3.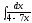
4.
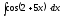 5.
5.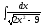 6.
6.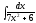
7.
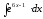 8.
8.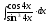 9.
9.
Вариант №15
1.
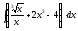 2.
2.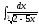 3.
3.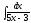
4.
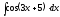 5.
5.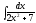 6.
6.
7.
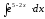 8.
8.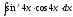
Вариант №16
1.
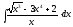 2.
2.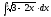 3.
3.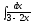
4.
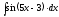 5.
5.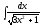 6.
6.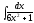
7.
 8.
8.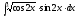
Вариант №17
1.
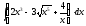 2.
2.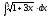 3.
3.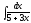
4.
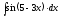 5.
5.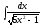 6.
6.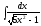
7.
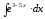 8.
8.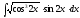
Вариант №18
1.
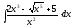 2.
2.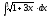 3.
3.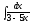
4.
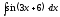 5.
5.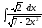 6.
6.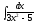
7.
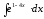 8.
8.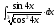
Вариант №19
1.
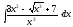 2.
2.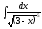 3.
3.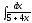
4.
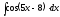 5.
5.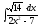 6.
6.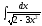
7.
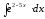 8.
8.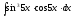
Вариант №20
1.
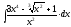 2.
2.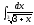 3.
3.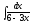
4.
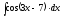 5.
5.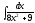 6.
6.
7.
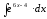 8.
8.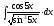
Вариант №21
1.
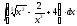 2.
2. 3.
3.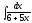
4.
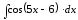 5.
5.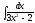 6.
6.
7.
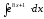 8.
8.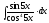
Вариант №22
1.
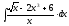 2.
2.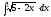 3.
3.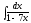
4.
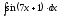 5.
5.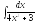 6.
6.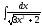
7.
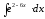 8.
8.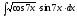
Вариант №23
1.
 2.
2.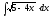 3.
3.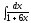
4.
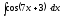 5.
5.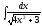 6.
6.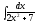
7.
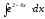 8.
8.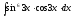
Вариант №24
1.
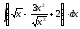 2.
2.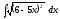 3.
3.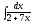
4.
 5.
5.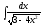 6.
6.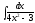
7.
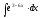 8.
8.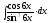
Вариант №25
1.
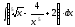 2.
2.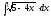 3.
3.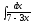
4.
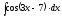 5.
5.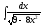 6.
6.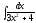
7.
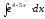 8.
8.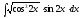
Задание 4.
Задачи N1-5 индивидуальные по указанным темам.
Задачи N6-8 имеют следующие условия:
Задача N6. Задан закон распределения случайной величины Х (в первой строке таблицы даны возможные значения величины Х, а во второй - вероятности p этих возможных значений). Найти :
1) математическое ожидание М(х);
2) дисперсию D(x);
3) среднее квадратическое отклонение (x). Начертить график закона
распределения и показать на нем вычисленные М(х) и (x).
Задача N7. Вероятность того, что деталь окажется бракованной, равна p. Составить закон распределения для случайной величины Х - числа бракованных деталей в выборке из n деталей. Определить вероятность того, что в выборке будет бракованных :
1) ровно k деталей; 2) не более k деталей; 3) ни одной бракованной.
Задача N8. Случайная величина Х задана функцией распределения F(x). Требуется найти плотность распределения вероятностей f(x), математическое ожидание М(х), дисперсию D(x). Нарисовать графики функций y = F(x), y = f(x).
Вариант 1
1. Студент идет на экзамен, подготовив только 15 вопросов из 18. Экзаменатор задает студенту 3 вопроса. Найти вероятность того, что студент знает все три вопроса.
2. Наудачу выбрано натуральное число, не превосходящее 20. Найти вероятность того, что это число кратно 5.
3. Вероятность попадания в мишень для первого стрелка 0,8, а для второго - 0,6. Стрелки независимо друг от друга сделали по одному выстрелу. Какова вероятность того, что :
а) в мишень попадет хотя бы один из стрелков;
б) ни один из стрелков не попадет в мишень.
4. Имеется 10 одинаковых урн, из них три урны с номером 1, в которых находится 7 белых и 8 красных шаров, одна урна с номером два с 1 белым и 9 красными шарами и шесть урн с номером три с 9 белыми и 1 красным шаром. Определить вероятность того, что шар, вынутый из произвольной урны, окажется белым.
5. Книга издана тиражом в 50000 экземпляров. Вероятность того, что в книге имеется дефект брошюровки, равна 0,0001. Найти вероятность того, что тираж содержит 5 неправильно сброшюрованных книг.
6
|
Х |
28 |
32 |
34 |
36 |
|
p |
0,1 |
0,2 |
0,2 |
0,5 |
7. n=6; p=0,2; k=4
