Литература от Абакумова ч1 / 0917183_820FF_lekcii_po_processam_i_apparatam_himicheskih_tehnologiy

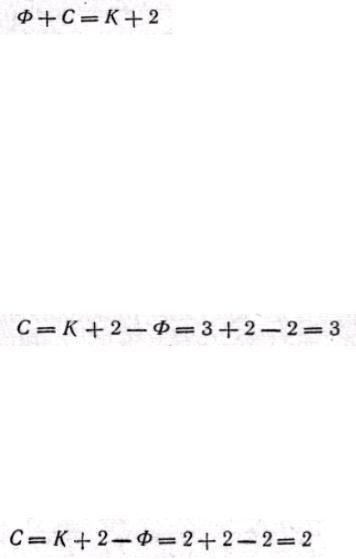
Парциальные давления. Состав газовых смесей часто выражают через парциальные давления компонентов, пропорциональные концентрациям последних и не зависящие от температуры газа.

3.2 Равновесие при массопередаче

Правило фаз. Знание равновесия в процессах массопередачи позволяет установить пределы, до которых могут протекать эти процессы. В основе равновесия лежит известное правило фаз:

где Ф — число фаз; С — число степеней свободы, т. е. число независимых переменных, значения которых можно произвольно изменять без нарушения числа иливида (состава) фаз в системе; K — число компонентов системы.

Правило фаз указывает число параметров, которое можно менять произвольно (в известных пределах) при расчете равновесия в процессах массообмена. Применим это правило к указанным выше двум группам процессов массопередачи: 1) каждая из двух взаимодействующих фаз содержит, помимо распределяемого компонента, инертный компонент-носитель (абсорбция, экстракция и др.); 2) в каждой из двух фаз компонент-носитель отсутствует (ректификация).

В первом случае система, состоящая из двух фаз (Ф = 2) и трех компонентов — распределяемого вещества и двух веществ — носителей, согласно правилу фаз, имеет три степени свободы:

Таким образом, число степеней свободы равно общему числу компонентов, включая компоненты-носители. В этом случае можно произвольно изменять общее давление (Р), температуру (t) и концентрацию одной из фаз по распределяемому компоненту (ХА или уА). Следовательно, при данных температуре и давлении (t = const и Р = const) некоторой концентрации одной из фаз соответствует строго определенная концентрация другой фазы.

Во втором случае система, состоящая из двух фаз (Ф = 2) и двух распределяемых компонентов (К = 2), имеет только две степени свободы:

Принимая во внимание, что процессы массопередачи осуществляются обычно при постоянном давлении (Р = const), можно заключить, что в данном случае с изменением концентрации фазы (ХА) должна меняться температура. Вместе с тем, если бы такой процесс проводился при t=const, то различным концентрациям фазы отвечали бы разные давления.

Зависимости между независимыми переменными могут быть изображены в плоских координатах в виде так называемых ф а з о в ы х диаграмм. В расчетах по массопередаче используют диаграммы зависимости давления от концентрации (при t = const), температуры от концентрации (при Р =const) и диаграммы зависимости между равновесными концентрациями фаз, приведенные ниже.

51

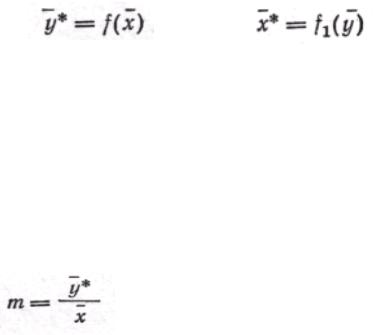
Фазовое равновесие. Линия равновесия. Рассмотрим в кглестве примера процесс массопередачи, в котором аммиак, представляющий собой распределяемый компонент, поглощается из его смеси с воздухом чистой водой, т. е. в виду отсутствия равновесия переходит из газовой фазы Фу, где его концентрация равна y, в жидкую фазу Фж, имеющую начальную концентрацию х = 0. С началом растворения аммиака в воде начнется переход части его молекул в обратном направлении со скоростью, пропорциональной концентрации аммиака в воде и на границе раздела фаз. С течением времени скорость перехода аммиака в воду будет снижаться, а скорость обратного перехода возрастать, причем такой двусторонний переход будет продолжаться до тех пор, пока скорости переноса в обоих направлениях не станет равны друг другу. При равенстве скоростей установится динамическое равновесие, при котором не будет происходить видимого перехода вещества из фазы в фазу.

При равновесии достигается определенная зависимость между предельными, или равновесными, концентрациями распределяемого вещества в фазах для данных температуры и давления, при которых осуществляется процесс массопередачи.

В условиях равновесия некоторому значению х отвечает строго определенная равновесная концентрация в другой фазе, которую обозначим через у*. Соответственно концентрации у отвечает равновесная концентрация х*. В самом общем виде связь между концентрациями распределяемого вещества в фазах при равновесии выражается зависимостью:

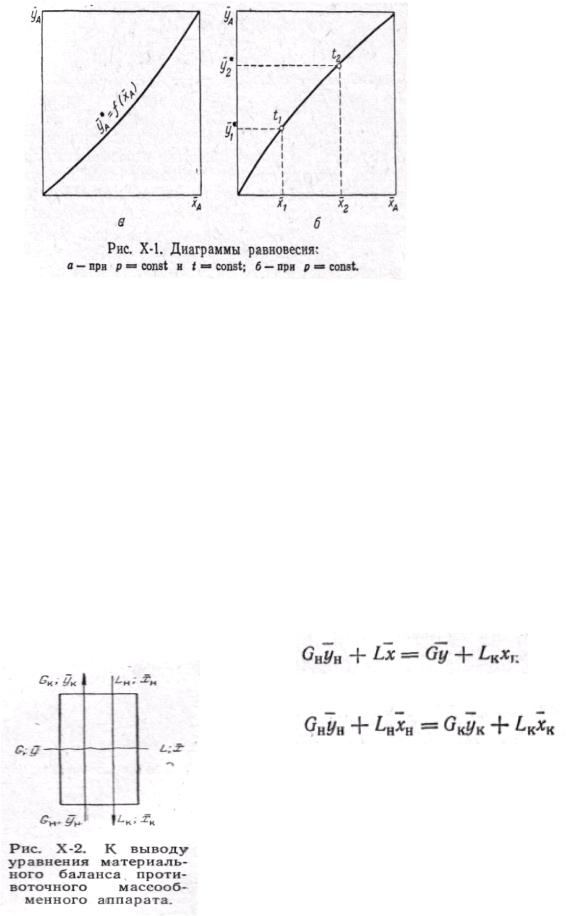
является кривой, как показано на рис. 1, либо в частном случае — прямой линией. На рис. 1,а показана равновесная кривая для системы с компонентаминосителями, выражающая зависимость равновесной концентрации, например в газовой фазе, от концентрации жидкой фазы при Р = const и t = const. На рис. 1,б приведен пример равновесной кривой для процесса ректификации, построенной при Р = const. Каждая точка кривой, как показано на рисунке,

(10)Коэффициент распределения выражает тангенс угла

наклона линии равновесия и для кривой линии равновесия является величиной переменной.

Материальный баланс. Рабочая линия. Рабочие концентрации распределяемого вещества не равны равновесным, и в действующих аппаратах никогда не достигают равновесных значений.

52

Зависимость между рабочими концентрациями, распределяемого вещества в

общем виде, является одинаковым для всех массообменных процессов и получается из их материальных балансов.

Рассмотрим схему массообменного аппарата, работающего в режиме идеального вытеснения при противотоке фаз (рис. 2). Пусть в процессе массопередачи из фазы в фазу, например из газовой фазы в жидкую, переходит только один

распределяемый компонент (скажем, аммиак).

Сверху в аппарат поступает LH кг/сек одной фазы (жидкой), содержащей xн вес. долей

распределяемого компонента, а снизу из аппарата удаляется LK кг/сек той же фазы, содержащей xк вес. долей распределяемого компонента. Снизу в аппарат поступает GH кг/сек другой фазы (газовой) концентрацией ун и сверху удаляется GK кг/сек этой фазы, имеющей концентрацию ук вес. долей распределяемого компонента.

Тогда материальный баланс по всему веществу и материальный баланс по распределяемому компоненту

Теперь 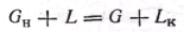напишем уравнения материального баланса для части аппарата от его нижнего конца до некоторого произвольного сечения, для которого расходы фаз составляют G и L кг/сек, а их текущие концентрации равны у и х соответственно.

Материальный баланс по всему веществу и материальный баланс по распределяемому компоненту

Решая это уравнение относительно у, получим

53

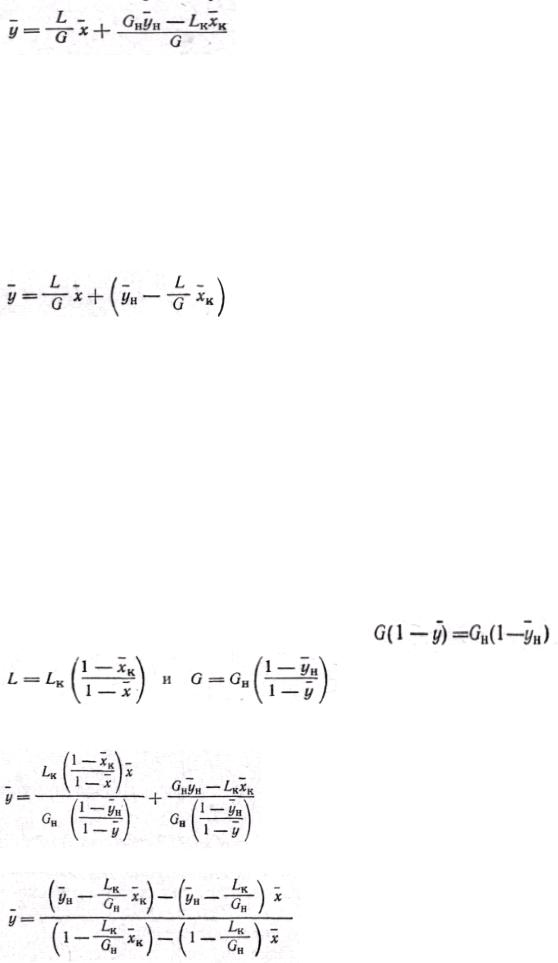
(11)

Уравнение (11) представляет собой у р а в н е н и е р а б о ч е й линии, выражающее связь между рабочими концентрациями распределяемого компонента в фазах для произвольного сечения аппарата.

Расходы фаз постоянны по высоте аппарата, например в процессах ректификации, когда числа молей компонентов, которыми обмениваются фазы, равны. В других случаях, если концентрации фаз мало изменяются по высоте аппарата, то расходы фаз по его высоте можно с достаточной для

практических целей точностью считать постоянными, т. е. принять L = const и G = const. При этом LK = L, GH =G и уравнение (11) приводится к виду:

(11а)

Вводя обозначения и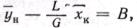находим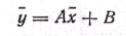(116) Выражения (11а) и (11б) являются уравнениями рабочей линии, которыми обычно пользуются при расчетах массообменных процессов.

Таким образом, рабочая линия представляет собой прямую, которая наклонена к горизонту под углом, тангенс которого равен А, и отсекает на оси ординат отрезок, равный В. Рабочая линия для всего аппарата ограничена точками с координатами хн и ук (верхний конец аппарата, рис. 2)'и ун и хк (нижний конец аппарата).

Если расходы фаз з н а ч и те л ьн о и з м е н я ютс я по высоте аппарата, то материальные балансы по компоненту-носителю для части аппарата от его нижнего конца до произвольного сечения (где концентрации фаз равны х и у ) выражаются уравнениями:

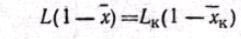и откуда

Подставив значения L и G в общее уравнение материального баланса (11), получим

Послесоответствующихпреобразований уравнениерабочейлиниипринимает вид:

(11в)

54

Из уравнения (11в) следует, что в рассматриваемом случае рабочая линия криволинейна.

3.3 Скорость массопередачи

Скорость массопередачи связана с механизмом переноса распределяемого вещества в фазах, между которыми происходит массообмен. Перенос вещества внутри фазы может происходить только путем

лекулярной диффузии вещество перемещается, строго говоря, лишь в неподвижной среде. В движущейся среде перенос вещества осуществляется как молекулярной диффузией, так и самой средой в направлении ее движения или отдельными ее частицами в разнообразных направлениях.

В турбулентном потоке перенос молекулярной диффузией преобладает только вблизи границы фазы. При турбулентном течении возникают нерегулярные пульсации скорости, под действием которых, наряду с общим движением потока, происходит перемещение частиц во всех, в том числе и в поперечном направлении. Конвективный перенос вещества, осуществляемый под действием турбулентных пульсаций, часто называют т у р б у л е н т н о й диффузией.

3.3.1 Молекулярная диффузия.

Молекулярной. диффузией называется перенос распределяемого вещества, обусловленный беспорядочным движением самих молекул. Молекулярная диффузия описывается п е р в ы м за коном Фика,

согласно которому количество вещества dM про-диффундировавшего за время dr через элементарную поверхность dF (нормальную к направлению диффузии) пропорционально градиенту-концентрации dc/dn этого вещества:

(12)или (12а)

Из выражения (2а) следует, что удельный поток вещества, переносимого молекулярной диффузией через единицу поверхности (F — 1) в единицу времени (τ = 1), или скорость молекулярной диффузии, составляет

(13)

По своей структуре закон Фика аналогичен закону Фурье, описывающему передачу тепла теплопроводностью, причем аналогом градиента температур является в данном случае г р а д и е н т конц е н т р а ц и й , представляющий собой изменение концентрации диффундирующего вещества на единицу длины нормали между двумя поверхностями постоянных, но различных концентраций.

55

Коэффициент пропорциональности D в выражении закона Фика называется

первого закона Фика указывает на то, что молекулярная диффузия всегда протекает в направлении уменьшения концентрации распределяемого компонента.

Согласно уравнению (12), коэффициент диффузии выражается следующим образом:

откуда (до сокращения одноименных величин)

вытекает физический смысл-D. Коэффициент диффузии показывает, какое количество вещества диффундирует в единицу времени через единицу поверхности при градиенте концентрации, равном единице.

Возвращаясь к аналогии с теплопередачей, можно отметить, что коэффициент диффузии D является аналогом коэффициента температуропроводности а. Коэффициент молекулярной диффузии представляет собой физичес к у ю к о н с т а н т у , характеризующую способность данного вещества проникать вследствие диффузии в неподвижную среду. Величина D таким образом не зависит от гидродинамических условий, в которых протекает процесс.

Значения коэффициента диффузии D являются функцией свойств распределяемого вещества, свойств среды, через которую оно диффундирует, температуры и давления. Обычно величины D возрастают с увеличением* температуры и понижением давления (для газов). В каждом конкретном случае значение D определяют по опытным данным или по теоретическим и полузмпирическим уравнениям* с учетом температуры и давления, при которых протекает процесс диффузии.

Коэффициенты диффузии газа в среду другого газа имеют значения 0,1 — 1 см2/сек, а при диффузии газа в жидкость они в 104 —105 раз меньше и составляют примерно 1 см2/сутки. Таким образом, молекулярная диффузия является весьма медленным процессом, особенно в жидкостях.

3.3.2 Турбулентная диффузия.

Количество вещества dMт, переносимого в пределах фазы вследствие турбулентной диффузии, принимается, по аналогии с молекулярной диффузией, пропорциональным поверхности dF, времени dτ и градиенту концентрации dc/dn и определяется по уравнению

(16)

где εд — коэффициент турбулентной диффузии.

Соответственно удельный поток вещества, переносимого путем турбулентной диффузии через единицу поверхности в единицу времени, или с к о р о с т ь т у р б у л е н т н о й д и ф ф у з и и , составляет

56

(17)

Коэффициент турбулентной диффузии εд показывает, таким образом, какое количество вещества передается посредством турбулентной диффузии в единицу времени через единицу поверхности при градиенте концентрации, равном единице.

Коэффициент εд выражается в тех же единицах, что и коэффициент молекулярной диффузии D, т. е. в м2/сек. Однако в отличие от D коэффициент турбулентной диффузии εд не является физической константой; он зависит от г и д р о д и н а м и ч е с к и х у с л о в и й , определяемых в основном скоростью потока и масштабом турбулентности.

3.3.3 Конвективный перенос.

Скорость конвективного переноса вещества вместе с самой средой в направлении, совпадающем с направлением общего потока, равна

(18)

где ω — скорость потока жидкости, газа или пара; С — коэффициент пропорциональности.

Суммарный перенос вещества в движущейся среде, по аналогии с теплообменом, называют к о н в е к т и в н ы м массообменом (конвективной диффузией). Распределение концентраций при конвективном массообмене определяется в самом общем виде дифференциальным уравнением массообмена в движущейся среде.

Дифференциальное уравнение массообмена в движущейся среде. Выделим в потоке данной фазы элементарный параллелепипед с ребрами dx, dy и dz, ориентированными относительно осей координат, как показано на рис.

4. Рассмотрим материальный баланс по распределяемому веществу для параллелепипеда при установившемся массообмене. Распределяемое вещество проходит сквозь грани параллелепипеда как путем конвективного переноса, так и путем молекулярной диффузии.

Обозначим концентрацию распределяемого вещества в плоскости левой грани параллелепипеда площадью dydz

через с и проекции скорости на оси координат для данного элемента (точки) потока — через wx, wy и wz соответственно.

57

Тогда количество вещества, поступающего только путем конвективного переноса через площадь dydz, т, е. в направлении оси х, за время dτ составляет

На противоположной грани параллелепипеда скорость в направлении оси х

параллелепипеда выходит путем конвективного переноса количество вещества

Разность между количествами вещества, прошедшего через противоположные грани параллелепипеда за время dτ в направлении оси х, равна

где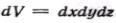— объем элементарного параллелепипеда.

В литературе это уравнение часто носит название диффе ре нц иал ьно го у р а в н е н и я к о н в е к т и в н о й диффузии.

Аналогично в направлении осей у и z:

Таким образом, содержание распределяемого вещества в объеме параллелепипеда изменится за время dr вследствие перемещения вещества только путем конвективного переноса на величину

или в развернутом виде

Согласно уравнению неразрывности потока для установившегося движения

Следовательно, предыдущее выражение dMK примет вид

(А)

Количество распределяемого вещества, поступающего в параллелепипед только путем молекулярной диффузии через грань dydz за время dτ в соответствии с уравнением (18) составляет

Количество вещества, выходящего за то же время путем молекулярной диффузии через противоположную грань

58

Разность между количествами продиффундировавшего через противоположные грани параллелепипеда вещества в

направлении оси х за время dτ равна

Аналогично в направлении осей у и z:

Количество распределяемого вещества в объеме всего параллелепипеда за время di изменится при переносе путем молекулярной диффузии на величину

(Б)

Изменение количества распределяемого вещества за счет конвективного переноса в объеме параллелепипеда (его накопление или убыль) должно компенсироваться соответственно отводом или подводом такого же количества вещества через грани параллелепипеда путем молекулярной диффузии, т. е. должно соблюдаться условие

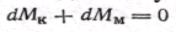В противном случае концентрация распределяемого вещества в любой точке параллелепипеда стала бы изменяться во времени, в то время как при установившемся процессе она является только функцией координат точки, т. е. с = f(x, у, z). Такимобразом

и в соответствии е выражениями (А) и (Б) получим

Уравнение (19) представляет собой д и ф ф е р е н ц и а л ь н о е у р а в н е н и е кон в е к т и в н о г о массообмена, или дифференциальное уравнение массообмена в движущейся среде. Оно выражает з а к о н р а с п р е д е л е н и я к о н ц е н т р а ц и и данного компонента в движущейся среде при установившемся процессе массообмена.

Для неустановившегося процесса массообмена (но протекающего в условиях стационарного потока фазы) левая часть уравнения (19) должна быть

по структуре аналогично дифференциальному уравнению конвективного теплообмена (уравнению Фурье — Кирхгофа). Отличием является то, что в

59

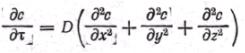
уравнение (20) вместо температурного градиента входит градиент концентрации, а вместо коэффициента температуропроводности α — коэффициент молекулярной диффузии D.

При массообмене в неподвижной среде wx = wy = wz = 0 и конвективная составляющая в левой части уравнения (20) равна нулю, и уравнение обращается в дифференциальное уравнение молекулярной диффузии

(21) Уравнение (21) носит название в т о р о г о

з а к о н а Фика.

3.3.4 Термодиффузия.

При наличии перепада темперагур в фазе возникает перенос, обусловленный градиентом температур, который называется термодиффузиеи. В этом случае более тяжелый компонент смеси перемещается в направлении градиента температур, т. е. в часть объема с более низкой температурой, а более легкий компонент в противоположном направлении. В результате у холодной поверхности фаза обогащается более тяжелым, а у горячей — более легким компонентом.

Явление термодиффузии наблюдается в некоторых процессах массообмена и эффективно используется для получения изотопов, методы разделения которых описываются в специальной литературе.

3.4 Механизм процессов массопереноса.

Трудности чисто теоретического анализа и расчета массопереноса обусловлены сложностью механизма переноса к границе раздела фаз и от нее путем молекулярной и турбулентной диффузии и недостаточной изученностью гидродинамических закономерностей турбулентных потоков, особенно вблизи подвижной границы раздела фаз.

На рис. 5 приведена схема, поясняющая процесс массопередачи между жидкостью и газом (паром) или между двумя жидкостями. Фазы движутся с некоторой скоростью друг относительно друга и разделены подвижной поверхностью раздела.

Пусть перенос распределяемого вещества М (например, аммиака) происходит в условиях турбулентного движения фаз. Примем также, что вещество переходит из фазы Фу, где концентрация вещества М выше равновесной (смеси аммиака с воздухом), в фазу Фх, например в воду. Таким образом, осуществляются процесс массоотдачи из основной массы фазы Фу к поверхности раздела фаз и процесс массоотдачи от поверхности раздела к основной массе фазы Фх.

В результате этих частных процессов, а также преодоления сопротивления переносу через самую поверхность раздела фаз (если оно имеет заметную величину) происходит процесс массопередачи — переход вещества из одной фазы в другую.

60