Лабораторная работа № 14

Работа с матрицами Решение системы линейных алгебраических уравнений

Цель работы: Освоение методики решения системы линейных алгебраических уравнений (СЛАУ) с помощью пакета Mathcad.

Основные операции с векторами и матрицами

1. Задайте вектор x размерности 31.

• Наберите х: (икс двоеточие).

• Нажмите кнопку на панели инструментов Матрица.

• Укажите размерность вектора 31.

• Нажмите ОК.

• Заполните заготовку любыми числами. Для перемещения по значениям вектора (матрицы) используйте клавиши перемещения курсора и клавишу <Tab>.

2. Задайте вектор y той же размерности.

3. Вычислите скалярное произведение векторов.

• Наберите x*y=

4. Вычислите сумму векторов.

• Наберите x+y=

5. Вычислите сумму и произведение матриц.

• Задайте две квадратные матрицы A и B одинаковой размерности, например 22.

• Вычислите их сумму и произведение.

6. Вычислите обратную матрицу

• Наберите A^–1.

7. Вычислите определитель матрицы А

• Воспользуйтесь кнопкой на панели инструментов Матрица.

Решение СЛАУ

8. Решите систему уравнений

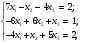
Решение

Решим систему методом обратной матрицы. Примем следующие обозначения:

A – матрица коэффициентов системы;

B – вектор свободных членов;

X – вектор результатов решения.

1. Задайте матрицу А коэффициентов системы и вектор свободных членов:

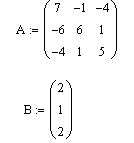
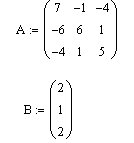
2. Вычислите определитель матрицы А, чтобы убедиться, что решение существует.

Если определитель отличен от нуля, то система имеет однозначное решение.

3. Чтобы найти вектор X, наберите X:=A^-1.

4. Для отображения на экране результата решения – матрицы 3×1 – введите с клавиатуры X= и нажмите клавишу <Enter>.

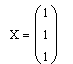
5. Чтобы вывести на экран значения X₁, X₂, X₃, выполните следующее:

• Укажите системе, что нумеровать элементы матриц и векторов мы хотим с 1 (по умолчанию с 0). Для этого выберите пункт меню Инструменты – Параметры документа… И в окне Параметры документа во вкладке Встроенные переменные установите начальный индекс массивов 1.

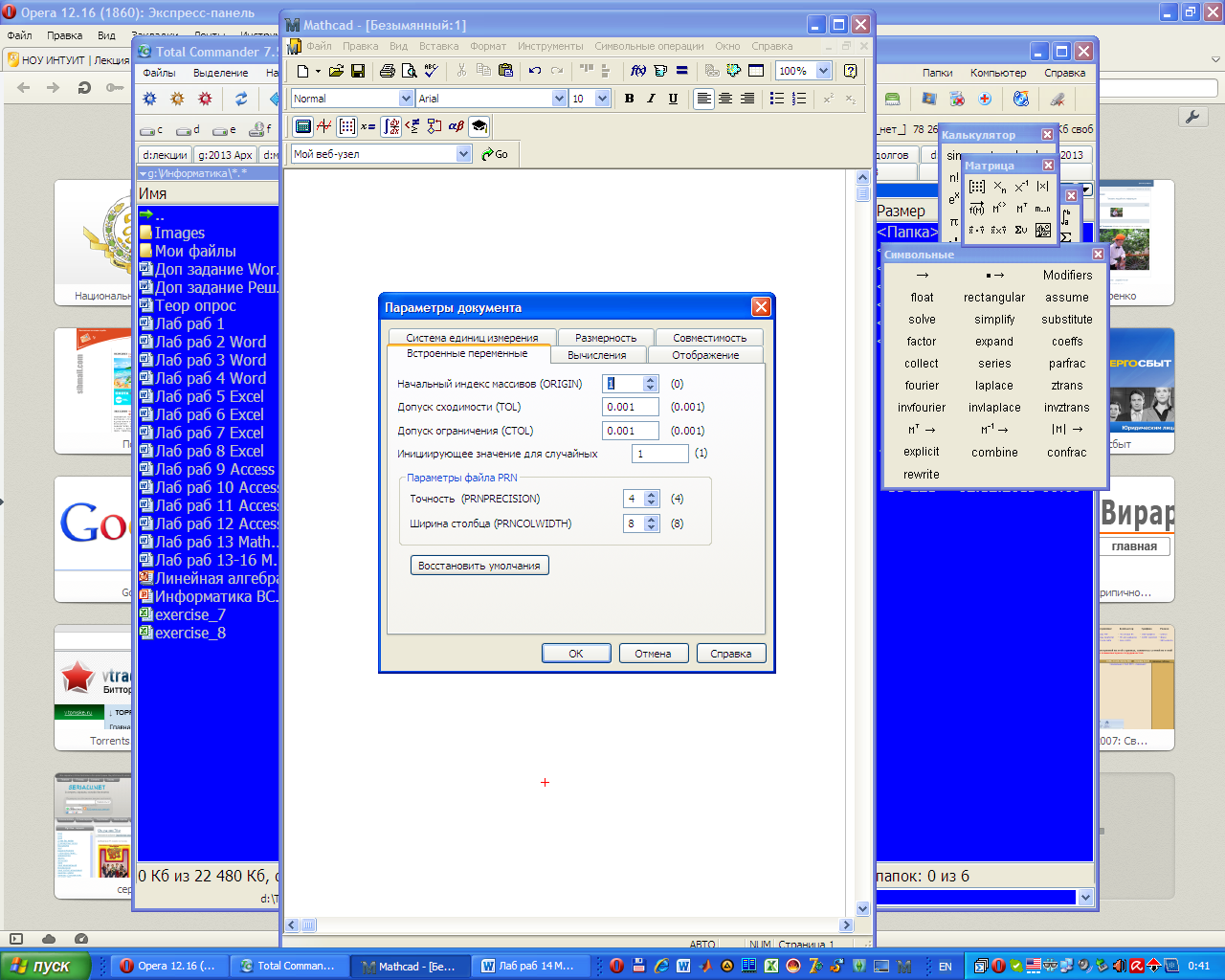
• Введите с клавиатуры X[1= (икс квадратная скобка 1 =), нажмите <Enter>. На экране появится X₁=1.

• Таким же образом получите значения остальных корней.

Самостоятельно

Решить систему линейных уравнений: