10. Прямая и двойственная задачи. Правила составления двойственной задачи.

При составлении двойственных задач используют следующие правила.

Правило 1.Во всех ограничениях исходной задачи свободные члены должны находиться в правой части, а члены с неизвестными — в левой.

Правило 2.Ограничения-неравенства исходной задачи должны быть записаны так, чтобы знаки неравенств у них были направлены в одну сторону.

Правило 3. Если знаки неравенств в ограничениях исходной задачи «≤», то целевая функция F(X) =c0+ c1x1 + с2х2 + ... + спхп должна максимизироваться, а если « ≥», то минимизироваться.

Правило 4.Каждому ограничению исходной задачи соответствует неизвестное в двойственной задаче; при этом неизвестное, отвечающее ограничению-неравенству, должно удовлетворять условию неотрицательности, а неизвестное, отвечающее ограничению-равенству, может быть любого знака.

Правило 5.Целевая функция двойственной задачи имеет вид

Z(Y) = c0+ b1y1 + ... + bmym, где c0 ―свободный член целевой функции F(X) исходной задачи; b1, ..., bт — свободные члены в ограничениях исходной задачи, при этом bi ― свободный член именно того ограничения, которому соответствует неизвестная yi; y1, у2, ..., ут — неизвестные в двойственной задаче.

Правило 6. Целевая функция Z(Y) двойственной задачи должна оптимизироваться противоположным по сравнению с F(X) образом, т.е. если F(X)→ max, то Z(Y) → min, и если F(X) →min, то Z(Y)→ max.

Правило7. Каждому неизвестному xj, j= 1, 2, ..., п исходной задачи соответствует ограничение в двойственной задаче. Совокупность этих п ограничений (вместе с условиями неотрицательности неизвестных yi, соответствующих ограничениям-неравенствам исходной задачи) образует систему ограничений двойственной задачи. Все ограничения двойственной задачи имеют вид неравенств, свободные члены которых находятся в правых частях, а члены с неизвестными y1, y2, ..., ут — в левых. Все знаки неравенств имеют вид «≥», если Z(Y)→ min, и «≤», если Z(Y)→ max.

Коэффициенты, с которыми неизвестные y1, y2, ..., ут входят в ограничение, соответствующее неизвестному хj, совпадают с коэффициентами при этом неизвестном хj в ограничениях исходной задачи, а именно: коэффициент при yi совпадает с тем коэффициентом при хj, с которым хj входит в ограничение исходной задачи, соответствующее неизвестному уi.

11. Связь между решениями прямой и двойственной задач. Теоремы двойственности.

Иногда для нахождения решения ЗЛП можно использовать теорему двойственности, согласно которой каждая ЗЛП можно определенным образом сопоставить с другой ЗЛП, называемой двойственной (ДЗ) по отношению к исходной задаче (ИЗ).

Связь взаимодействующих задач заключается в том, что решение одной из них (оптимальное) можно получить непосредственно из решения другой, используя теоремы двойственности.

Правила составления ДЗ (в стандартной и смешанной формах):

1. число переменных 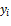в ДЗ = числу ограничений в ИЗ (и наоборот)

2. матрицы коэффициентов 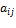в системе ограничений являются транспортированным друг к другу (замена строк столбцами)

3. коэффициенты при переменных ЦФ одной задачи являются свободными членами системы другой

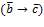
4. ЦФ ИЗ задается на max, а ЦФ ДЗ задается на min

5. в ИЗ все неравенства виды 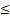, а в ДЗ

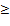
6. условия неотрицательности задаются в обеих задачах

Если ЗЛП задана в смешанном (общем) виде, то пункты 5 и 6:

• если переменная 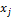может принимать лишь неотрицательное значение 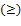, то 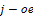условие в системе ДЗ является неравенством

• если переменная 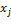не ограничена по знаку, то 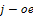ограничение в системе ДЗ является равенством

• если 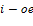ограничение в ИЗ является неравенством, то переменная 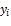в ДЗ должна быть неотрицательной

• если 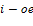ограничение в ИЗ является равенством, то переменная 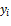в ДЗ знакопеременна

Замечание: если в ИЗ ЦФ максимизируется, а система ограничений содержит неравенства разного смысла, то приводим всех их к виду

Теоремы двойственности:

Связь между оптимальным решением ИЗ и ДЗ устанавливается с помощью теорем двойственности. Обозначим – ЦФ РФ

1 теорема.

1. если одна из двойственных задач имеет оптимальный план, то и другая задача имеет оптимальный план, причем значение ЦФ обеих задач при оптимальных планах равны

2. если ЦФ ИЗ не ограничена, то ДЗ не имеет дополнительного плана (нет решений)

3. если ИЗ не имеет допустимого плана, то ЦФ ДЗ не ограничена

2 теорема.

план ИЗ и план являются оптимальными планами тогда и только тогда, когда выполняется условие:

3 теорема.

компоненты оптимального решения ДЗ равны значениям частной производной ЦФ по соответствующим аргументам:

Другими словами: – предельная оценка вклада ресурса в суммарный доход F при оптимальном решении (прирост дохода при увеличении ресурса i на 1 при условии оптимального использования ресурсов)

12. Экономическая интерпретация двойственной задачи. Свойства двойственных оценок.

Из последней симплексной таблицы числового решения исходной задачи, на основании теорем двойственности, находят оптимальное значение целевой функции , а также соответствующие ей значения основных и дополнительных переменных двойственной задачи. Основные переменные двойственной задачиназываются «теневыми ценами» и характеризуют степень дефицитности единицы соответствующего ресурса.

Экономический смысл и соответствие переменных прямой и двойственной задач можно представить в виде следующей схемы:

результат	Переменные прямой задачи										затраты
	основные					дополнительные
	выпуск j-й продукции					остаток i -го ресурса
		…		…			…		…
		…		…			…		…
		…		…			…		…
	убыточность j-й продукции					Теневые цены i -го ресурса
	продукция (выход)					ресурсы (вход)
	дополнительные					основные
	Переменные двойственной задачи

Рис. Соответствие переменных прямой и двойственной задач

Таким образом, схема соответствия для переменных прямой и двойственной задач состоит из четырех квадрантов, характеризующих для продукции: количество выпускаемой продукции и ее убыточность (безубыточность), а для ресурсов - величину остатка ресурса и его теневую цену.

Продукция и используемые для ее производства ресурсы обладают свойствами допустимости (неотрицительности) и оптимальности (при которых целевые функции прямой и двойственной задач принимают соответствующие экстремальные значения).

Основные свойства двойственных оценок:

Свойство 1. Положительную двойственную оценку имеют лишь дефицитные ресурсы, т.е. те, которые полностью используются в производстве. Для недефицитных ресурсов, имеющих резерв (остаток), двойственная оценка равна нулю. Таким образом, оценки выступают как мера дефицитности ресурсов. Использование данного свойства позволяет вскрыть "узкие места", сдерживающие рост производства, помогает выбрать правильное решение, если предполагается расширение производства и требуется привлечение дополнительных ресурсов.

Кроме того, для тех типов продукции, которые вошли в оптимальный план, дополнительные двойственные оценки равны нулю, т.е. их выпуск не приносит убытка; т.е. типы продукции, которые не вошли в оптимальный план, были бы убыточными в случае их производства.

Свойство 2. Переменные двойственной задачи используются для определения влияния изменения запасов ресурсов, а также введения в производство тех типов продукции, которые не вошли в оптимальный план, на целевую функцию. Изменение ресурса, по которому есть резерв, не вызовет изменения целевой функции. Увеличение или уменьшение дефицитного ресурса на единицу приведет к увеличению или уменьшению целевой функции на величину соответствующей двойственной оценке.

Следует иметь в виду, что при увеличении дефицитного ресурса на единицу прирост целевой функции достигается за счёт перераспределения всех ресурсов по видам продукции, что приводит к количественным изменениям в оптимальном плане. Эти изменения могут быть определены при помощи последней симплексной таблицы на основании коэффициентов замещения при дополнительных небазисных переменных (т.е. рассматриваются столбцы дефицитных ресурсов). При этом положительные коэффициенты означают увеличение значений соответствующих базисных переменных, а отрицательные - уменьшение.

Свойство3. Двойственные оценки применяются в расчетах взаимозаменяемости ресурсов.

Взаимозаменяемость определяется по соотношению двойственных оценок. Следует подчеркнуть, что эквивалентная замена одних ресурсов другими приведёт к изменению оптимального плана, но значение целевой функции сохранится.

Свойство4. На основании уже полученного решения задачи можно ответить на вопрос о целесообразности включения в модель нового (n+1)-го типа продукции, для которого известны нормы расхода ресурсов и цена: a_in+l (i=) и P_n+l. Если , (n+l)-ый тип продукции убыточен, то включать его в модель нецелесообразно, иначе - целесообразно.

13. Анализ оптимального решения ЗЛП.

Анализ оптимального решения заключается в решении задачи оптимизации, в том числе параметрической и структурной. Анализ оптимального значения переменных задачи и исследование устойчивости структуры оптимального плана основываются на использовании информации, содержащейся в последней симплекс-таблице.

Экономический анализ предполагает решение 3 задач:

1. нахождение оптимального решения 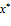и проведение экономического анализа по последней симплекс-таблице

2. исследование параметрической устойчивости: определение изменения параметров задачи 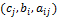при которых сохраняется базис (состав базисных переменных), однако оптимальное решение и ЦФ могут менять свои значения

3. исследование структурной устойчивости

Анализ оптимального значения переменных. Из последней симплексной таблицы находят оптимальное значение целевой функции F(x*), а также соответствующие ему значения основных (j=) и дополнительных (i=) переменных. Каждая из этих переменных представляет собой важную характеристику полученного оптимального плана. Состав и значения основных переменных определяют номенклатуру и количество продукции, при которых будет достигнута максимальная стоимость продукции. Значения дополнительных переменных показывают резервы (остатки) по рассматриваемым видам ресурсов.

В последней симплексной таблице также имеются соответствующие оптимальному решению задачи значения переменных двойственной задачи, дающие ответ на ряд практически важных вопросов.

Замечание: значение -строки можно проверить используя формулу:

Количественные изменения в оптимальном плане могут быть определены при помощи последней симплексной таблицы решения задачи на основании коэффициентов замещения при основных небазисных переменных. При этом положительные коэффициенты показывают уменьшение, а отрицательные - увеличение значений соответствующих переменных.

Исследование устойчивости оптимального решения - это изучение влияния изменений отдельно взятых параметров модели (коэффициентов целевой функции, технико-экономических коэффициентов, объёмов ограничений по ресурсам и др.) и её структуры (введение новых ограничений и переменных или их сокращение) на показатели оптимального решения.

Исследование параметрической устойчивости, основано на свойствах оптимальности, допустимости и безубыточности выпускаемой продукции. Эти свойства позволяют определить границы изменения , соответственно, цен за единицу изделий , объемов ресурсов и норм расхода ресурсов на производство единицы изделия при которых структура (номенклатура) оптимального плана выпуска продукции не изменится.

Структурная устойчивость оптимального плана предполагает решение вопроса о целесообразности включения в модель новой основной переменной (нового вида продукции) в рамках ее безубыточности. Новый вид продукции будет безубыточен, если суммарная оценка дефицитности ресурсов, используемых на производство единицы продукции («внутренняя цена») будет не больше внешней цены Добавление в модель новых, ранее отсутствующих ограничений изменит структуру оптимального плана, если расход нового ресурса для оптимального плана выпуска продукции будет превосходить имеющийся его запас.

На основании экономического анализ оптимального решения прямой задачи и исследование параметрической и структурной его устойчивости необходимо указать пути повышения эффективности применяемых на предприятии технологий и используемых ресурсов.

14. Исследование устойчивости оптимального решения к изменению коэффициентов целевой функции.

Исследование устойчивости оптимального решения к изменению коэффициентов целевой функции основано на свойстве оптимальности .

Пусть , тогда

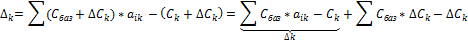
15. Исследование устойчивости оптимального решения к изменению запасов ресурсов.

Задача решается на основе свойства допустимости.

В задаче имеем следующие параметры:

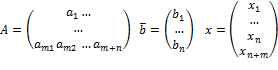
Эти параметры введены для задачи в канонической форме (базисной). В матричном виде:

Представим матрицу А в виде двух матриц:

Метод решения задач, основанных на формуле называется модифицированным симплекс-методом.

Таким образом, при решении ИЗ симплекс методом вычисляется матрица : Она располагается в последней симплекс-таблице на месте единичной матрицы в 1 симплекс-таблице.

С	баз	в				0	0	0
			Х1	Х2	Х3	Х4	Х5	Х6
	Х1
	Х2
	Х3

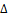
Пусть , тогда

Если все ресурсы изменять на , подставить их в соотношение и все неравенства будут положительными, то базис не изменится.