
13. Показательные и логарифм. уравнения
.docxПоказательные уравнения
Простейшие
показательные уравнения имеют вид:
![]() .
.
Уравнение
![]() при
при
![]() и
при
и
при
![]() корней
не имеет, так как показательная функция
всегда положительна.
корней
не имеет, так как показательная функция
всегда положительна.
Если в уравнении присутствуют показательные функции с разными основаниями, можно попытаться привести их к одному и тому же основанию. То же относится и к логарифмическим уравнениям.
-
 при
при
 ,
,
 ;
;
-
 .
.
|
§ 2. Методы решения показательных уравнений |
|
При решении показательных уравнений необходимо помнить, что решение любого показательного уравнения сводится к решению “простейших” показательных уравнений, то есть уравнений вида: 1. af(x)=ag(x) или 2. af(x)=b. Очевидно, что уравнение типа 2 сводится к уравнению типа 1 с помощью основного логарифмического тождества: 2! af(x)=
Уравнение (1) равносильно уравнению f(x)=g(x) при а 0, а 1. Этот переход называется потенцированием. |
|
Способы решения показательных уравнений |
|
1 тип: приведение к одному основанию левой и правой частей, применяя свойства степеней: а)
Проверка:
б)
Решение:
(х+5)(х–3)=(х+25)(х–7); х2+5х–3х–15=х2+25х–7х–175; 16х=160; х=10. Проверка:
х=10.
Ответ: х=10; в)
Решение:
Проверка:
Ответ: х=1; г)
Решение:
для
х Проверка:
х=0.
х= Ответ:
х= 2 тип – уравнения вида P(ax)=0, где P(y) – многочлен 2 или 3 степени, или уравнения, сводящиеся к ним. Такие уравнения решаются методом подстановки: ax=y, решаем уравнение P(y)=0, находим его корни yi и потом решаем простейшее уравнение ax= yi. Пример:
а)
Решение:
Обозначаем:
Получаем:
1.
2.
Проверка:
1.
2.
Ответ: х=2; х=–2; б)
Решение:
y1,2=–6 y1=4; y2=–16 (п.к.), т.к. 4х 0, 4х=4 х=1. Проверка:
Ответ: х=1; в)
Решение:
Пусть
Проверка:
x=20.
Ответ: х=20. г)
Решение:
Проверка:
x= х=1;
Ответ:
x= 3 тип – метод вынесения общего множителя за скобки: а)
Решение:
Проверка:
Ответ: х=0; б)
Решение:
Проверка:
Ответ: х=0; в)
Решение:
Проверка:
–3=–3 – верно. Ответ: х=2. 4
тип – уравнения вида
а)
Решение:
Делим на
Положим
Проверка:
х=0;
х= Ответ:
х=0; х= б)
Решение:
Проверка:
6=6 – верно;
Ответ:
|
|
Логарифмические уравнения Простейшие
логарифмические уравнения имеют вид:
§ 3. Методы решения логарифмических уравнений |
|
Решение любого логарифмического уравнения также сводится к решению одного или нескольких простейших логарифмических уравнений: 1) logaf(x)= logag(x); 2) logaf(x)=b. Уравнение (2) сводится к уравнению вида (1): logaf(x)= logaab. Уравнения вида (1) сводятся к решению уравнений f(x)= g(x) (потенцирование). При этом необходимо помнить, что уравнения logaf(x)= logag(x) и f(x)= g(x) не равносильны. При потенцировании происходит расширение области определения, а значит имеется опасность появления посторонних корней. Проверка – наилучшее средство против такой опасности. 1 тип – по определению логарифма: а)
Решение:
Проверка:
Ответ: х=5. б)
Решение:
Проверка: х=–1, log3(1–4+12)=2; log39=2; 2log33=2; 2=2 – верно; х=–3, log3(9–12+12)=2; log39=2; 2log33=2; 2=2 – верно. Ответ: х=–1, х=–3. в)
Решение:
Проверка:
Ответ: х=2. 2 тип – уравнения, которые с помощью логарифмических тождеств сводятся к простейшим уравнениям: а) lg(x–3)+lg(x–2)=1–lg5. Решение: lg[(x–3)(x–2)]=lg10–lg5; lg(x2–5x+6)=lg2; x2–5x+6=2;
x2–5x+4=0; x1,2= Проверка: х=4; lg(4–3)+ lg(4–2)=1– lg5; lg1+ lg2= lg2; lg2= lg2 – верно; х=1; lg(1–3)+ lg(1–2)1– lg5, так как выражение, стоящее под знаком логарифма, должно быть всегда положительным. Ответ: х=4; б)
Решение:
2 lg(4(х–3))= lg(3(7х+1)(х–6)); lg(4(х–3))2= lg(3(7х+1)(х–6)). Потенцируем: 16х2–96х+144=21х2–123х–18; –5х2+27х+162=0; 5х2–27х–162=0;
х1,2= Проверка:
х=9;
х= Ответ: х=9; в)
Решение.
Воспользуемся формулой
Проверка:
Ответ: х=27; г)
Решение:
Потенцируем:
(3х–11)(х–27)=1000; 3х2–92х–703=0. х1,2= Проверка:
1.
2.
Ответ: х=37. 3 тип – уравнения вида P(logax)=0, где P(y) – многочлен 2 или 3 степени, или уравнения, сводящиеся к ним. Эти уравнения решаются с помощью подстановки: y= logax. а)
Решение:
Проверка:
х=27;
9–6–3=0 – верно; х= 1+2–3=0 – верно. Ответ:
х=27; х= б)
Решение.
Прежде всего надо иметь в виду, что
если в уравнениях встречаются логарифмы
с разными основаниями, то их надо
привести к одному основанию с помощью
формулы:
В
данном случае переходим к основанию
5.
2y2+y–1=0;
y1=–1, y2= Проверка:
1)
2)
Ответ:
х= 5 тип – логарифмирование обеих частей уравнения. Пример:
Решение:
y2+2y–3=0. Решаем уравнение: y1=–3; y2=1; lgx=–3 или lgx=1, x=10–3; x=10. Проверка:
1)
106=106 – верно; 2)
Ответ: х=10–3; х=10. |

 ;
;
 ;
;
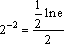 ;
;


 – ложно, так как подлогарифмическое
выражение не может быть отрицательным.
– ложно, так как подлогарифмическое
выражение не может быть отрицательным.