6. ОСНОВНЫЕ МОДЕЛИ ПОЛЗУЧЕСТИ

Явление ползучести, в общем случае связанное с изменением во времени t деформации и напряжения даже при постоянных внешней нагрузке и абсолютной температуре T, при одноосном напряженном состоянии часто называют простой ползучестью (или последействием), если при постоянном напряжении изменяется деформация ", и релаксацией, если при " = const изменяется напряжение . Экспериментальное исследование ползучести обычно проводят на растягиваемых образцах при , T = const, а результаты представляют в виде зависимости " от t (сплошная кривая на рис. 6.1), называемой кривой ползучести (иногда — кривой простого последействия). В общем случае на этой кривой можно выделить три характерных участка: I — стадия неустановившейся ползучести, когда ско-

рость (c) = d"(c) = d" деформации ползучести "(c) постепенно dt dt

уменьшается; I I — стадия установившейся ползучести при практически постоянном наименьшем значении (c), и I I I — стадия ускоряющейся ползучести, когда (c) непрерывно возрастает вплоть до разрушения образца. Напряжение, вызывающее разрушение образца за определенный промежуток времени при

T = const, называют пределом длительной прочности материала. При возрастании и/или T ординаты кривой ползучести увеличиваются (штриховая кривая на рис. 6.1), а продолжительность стадии установившейся ползучести сокращается. Для некоторых материалов при определенных условиях неустановившаяся ползучесть может непосредственно переходить в ускоряющуюся. Стадия установившейся ползучести вырождается на этой кривой в точку перегиба (штрихпунктирная линия на рис. 6.1). В случае существенной зависимости поведения материала при ползучести от изменения температуры говорят о термоползучести. Известно достаточно много различных подходов к построению математических моделей (ММ) простой ползучести. В од-

Рис. 6.1.

ном из подходов, характеризующих теорию старения, постулируют существование функции

= f1(",t,T),

которой при T = const в трехмерном пространстве ( , " и t) соответствует поверхность. Cечения этой поверхности плоскостями = const являются кривыми ползучести, плоскостями " = const — кривыми релаксации, а плоскостями t = const —

изохронными кривыми, аналогичными диаграммам деформирования, но с учетом накопленной к фиксированному моменту времени деформации ползучести. Изохронные кривые можно использовать для построения вариационной формы ММ ползучести подобно тому, как используются диаграммы деформирования в такой форме ММ, основанной на деформационной теории термопластичности (см. 4). Если кривые ползучести подобны, то

= ET (",T) 1(t).

Вэтом случае при ", T = const функция 1(t) описывает релаксацию. Для многих конструкционных материалов можно принять

1(t) = (1 + a1tb1 )−1, a1, b1 = const.

Пример 6.1. Пусть соотношение = f1(",t,T) при фиксированном значении температуры T имеет следующий конкретный вид:

"(c) = ( )n (t);

0

здесь функцию (t) определим соотношением

(t) = ktm,

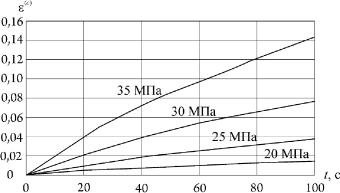
а 0 — произвольная величина напряжения, например, предел пропорциональности или текучести, взятый при температуре T. Для определенности примем: 0 = 10,0 МПа, n = 4, m = 0,8, k = = 2,9 × 10−5 1/с0,8. Пользуясь соотношением для "(c), можно построить семейство кривых ползучести для различных значений напряжения , например, 20 МПа, 25 МПа, 30 МПа, 35 МПа. Графики кривых ползучести представлены на рис. 6.2.

Рис. 6.2.

С другой стороны, из соотношения для "(c) можно получить

выражение

1

[ ]

= 0 "(c) ( (t))−1 n ,

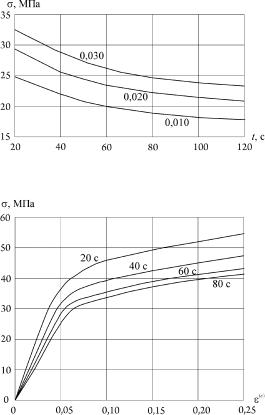
описывающее релаксацию напряжения при фиксированных уровнях деформации ползучести "(c), например, 0,010; 0,020; 0,030. Графики кривых релаксации напряжения представлены на рис. 6.3.

Последнее соотношение можно использовать и для построения семейства изохронных кривых ползучести, если менять значения деформации ползучести, но при этом зафиксировать определенные моменты времени, например, 20 с, 40 с, 60 с, 80 с. Графики изохронных кривых ползучести показаны на рис. 6.4.

Рис. 6.3.

Рис. 6.4.

#

Так как все изохронные кривые выходят из начала системы координат O", то, согласно теории старения, после накопления некоторой деформации ползучести "(c) при разгрузке до = 0 эта деформация должна полностью исчезнуть, что часто противоречит экспериментальным результатам. От такого противоречия свободна ММ, базирующаяся на теории течения и постулирующая существование зависимости

= f2( (c),t,T).

Эту зависимость часто удается представить в виде

(c) = d"(c) = ST ( ,T) 2(t), dt

что при постоянных и T после интегрирования по t позволяет получить соотношение

соответствующее кривой ползучести при фиксированных значениях и T, ординаты которой на рис. 6.1 отсчитываются от уровня "(0) деформации в начальный момент нагружения. Если2(t) = const, то эта ММ описывает лишь стадию установившейся ползучести.

При резком изменении более близкие к реальным результаты (по сравнению с рассмотренными ММ) дает ММ, основанная на теории упрочнения, постулирующей существование зависимости

(c) = f3( ,"(c),T).

При изменении знака вместо "(c) в качестве аргумента следует использовать параметр

t

∫

qc = | (c)|dt′,

0

аналогичный параметру Удквиста в ММ термопластичности и позволяющий учесть изотропное упрочнение материала на стадии неустановившейся ползучести. Более точное и полное описание процесса ползучести можно получить, если увеличить количество параметров, используемых в ММ. В частности, введением параметра, имеющего смысл среднего значения микронапряжений, удается учесть влияние анизотропного упрочнения материала, а путем использования параметра повреждаемости материала можно описать стадию ускоряющейся ползучести.

Учет предыстории процесса ползучести может быть также проведен в рамках так называемой наследственной теории ползучести.

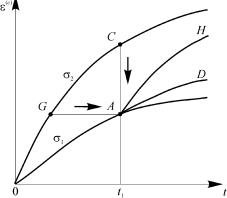
Пример 6.2. Рассмотрим процесс ползучести при ступенчатом нагружении. Вначале применим теорию течения. Представим, что образец испытывают на ползучесть в течение времени t1 при напряжении 1, а затем напряжение мгновенно увеличивается до величины 2. Кривые ползучести, соответствующие напряжениям 1, 2, представлены на рис. 6.5.

Рис. 6.5.

За время t1 деформация ползучести достигает величины "(Ac) (см. рис. 6.5), здесь точка A является точкой пересечения вертикальной линии, проведенной на расстоянии t1 от оси ординат

— оси, по которой в данном случае откладывают значения деформации ползучести, с кривой ползучести, соответствующей напряжению 1. Согласно теории течения после возрастания напряжения от 1 до 2 скорость деформации ползучести (c) будет численно равна тангенсу угла наклона касательной в точке C на графике кривой ползучести, соответствующей напряжению2. Точка C является точкой пересечения вертикальной линии, проведенной через точку A (см. рис. 6.5), с кривой ползучести, соответствующей напряжению 2. При t > t1 деформация ползучести изменяется (растет) в соответствии с кривой AD,

представляющей собой часть кривой ползучести при напряжении 2, перенесенной параллельно вниз из точки C в точку A.

Теперь рассмотрим процесс ползучести при ступенчатом нагружении в рамках теории упрочнения. В данном случае после возрастания величины напряжения от 1 до 2 скорость деформации ползучести (c) будет численно равна тангенсу угла наклона касательной в точке G на графике кривой ползучести, соответствующей напряжению 2 (см. рис. 6.5). Точка G является точкой пересечения горизонтальной линии, проведенной через точку A, с кривой ползучести, соответствующей напряжению 2. При t > t1 деформация ползучести изменяется (растет) в соответствии с кривой AH, представляющей собой часть кривой ползучести при напряжении 2, перенесенной параллельно вправо из точки G в точку A. #

Если за время порядка десятка или сотни секунд достигается значение "(c), сопоставимое с деформацией в начальный момент нагружения, то говорят о кратковременной ползучести. В этом случае для ряда конструкционных материалов при достаточно высоких значениях и T практически отсутствует стадия неустановившейся ползучести, а стадия установившейся ползучести может быть описана в рамках теории течения, если принять 2(t) = 1, т. е.

(c) = ST ( ,T).

Если в координатах T, построить кривую ACEB зависимости от T предела прочности материала (предела временного сопротивления) вр, выше которого материал разрушается в начальный момент нагружения, то в области ползучести BECD можно условно выделить подобласть BEF кратковременной ползучести (рис. 6.6). Левее линии CD расположена область, в которой ползучесть несущественна. Штриховые линии определяют зависимости от T предела длительной прочности материала при фиксированных значениях времени tр до его разрушения.

Обобщение рассмотренных ММ ползучести при одноосном напряженном состоянии на случай сложного напряженного состояния можно провести на основе следующих допущений.

58 Основные модели ползучести

Для теории течения

gт = 3ST ( и,T) 2(t), 2 и

а для теории упрочнения

3

gу = 2f3( и,qc,T).

Вопросы и задачи

1.Что называют простой ползучестью?

2.Нарисуйте график кривой ползучести и обозначьте на нем участки неустановившейся ползучести, установившейся ползучести и ускоряющейся ползучести.

3.Что называют пределом длительной прочности?

4.Что называют термоползучестью?

5.Напишите соотношение, характеризующее теорию старе-

ния.

6.Что такое изохронные кривые?

7.Напишите соотношение, характеризующее теорию течения.

8.Напишите соотношение, характеризующее теорию упрочнения.

9.Что называют кратковременной ползучестью?

10.Что называют пределом прочности (временного сопротивления) материала?

11.Сформулируйте основные допущения, позволяющие обобщать ММ ползучести при одноосном напряженном состоянии на случай сложного напряженного состояния.