
- •Предисловие
- •Введение
- •1. Простейшие модели пластического деформирования
- •2. Условие текучести
- •3. Модели термопластичности
- •4. Деформационная теория термопластичности
- •5. Сопоставление деформационной теории пластичности и теории пластического течения при сложном нагружении
- •6. Основные модели ползучести
- •Литература
3. МОДЕЛИ ТЕРМОПЛАСТИЧНОСТИ
Под термопластичностью понимают процесс развития в материале пластической деформации, протекающий в условиях изменения абсолютной температуры T. Иногда этот процесс называют неизотермической пластичностью. При построении математических моделей (ММ) термопластичности в качестве внутренних параметров термодинамического состояния обычно используют параметр Удквиста , учитывающий в поликристаллическом материале плотность микродефектов, и тензорный параметр ̂ с компонентами ij, i, j = 1, 2, 3, который пропорционален усредненному симметричному тензору плотности дислокаций и может рассматриваться как аналогичный тензору трансляции усредненный тензор микронапряжений, возникающих в скоплениях дислокаций. Эти параметры в случае твердого аморфного тела (например, полимера) могут иметь иной микромеханический смысл, но важным обстоятельством является их зависимость от компонент "(ijp) тензора пластической деформа-
ции, причем d = 0 и d ij = 0 при d"(ijp) = 0.
Любая ММ термопластичности в частном случае должна описывать эксперименты при одноосном нагружении, в которых проявляются упругие и пластические свойства материала, и подтверждаться результатами экспериментов при произвольном напряженном состоянии. На основании имеющихся экспериментальных данных можно сделать следующие заключения об общих свойствах такой модели:
– в бесконечно малой окрестности любой точки рассматриваемого тела приращение компонент тензора полной деформации
d"ij = d"ij(e) + d"ij(p) + d"ij(T), |
(3.1) |
где "(ije) и "(ijT) — компоненты тензоров упругой и температурной деформации соответственно;
Модели термопластичности |
|
25 |
||||
– в исходном состоянии материал изотропен, а при нагруже- |
||||||
нии изменение его объема происходит линейно-упруго, т. е. |
|
|||||
|
|
d"kk(p) = 0, |
|
|
|
|
d"V = d"kk = d"kk(e) + d"kk(T), |
k = 1,2,3, |
|
|
|||
@{ |
|
(T) |
(T) |
|
|
|
d kk =d ij ij =3 |
|
dT |
("V −"kk |
)+3{(d"V −d"kk |
), |
(3.2) |
@T |
||||||
где ij — компоненты тензора напряжений ̂; ij — символ Кронекера; "V — объемная деформация; { — объемный модуль упругости;
– компоненты девиатора упругой деформации линейно зависят от компонент sij девиатора напряжений, т. е.
(e) |
|
dsij |
|
@ dT |
|
|
|||
deij |
= |
|
|
− sij |
|
|
|
, |
(3.3) |
|
2 |
@T |
2 2 |
||||||
где — модуль сдвига;
– существует функция нагружения, определяющая для пластически деформируемой бесконечно малой окрестности рассматриваемой точки тела уравнение поверхности нагружения в пространстве напряжений в виде
f( ij,T, , ij) = 0. |
(3.4) |
Сплошную среду с указанными свойствами назовем термопластической средой.
Задаваемая (3.4) поверхность делит пространство напряжений на две части. При f( ij,T, , ij) < 0 бесконечно малая окрестность рассматриваемой точки тела деформируется упруго, т. е. d"(ijp) = 0, а напряженное состояние, соответствующее f( ij,T, , ij) > 0, не может быть реализовано.
Если левая часть (3.4) не зависит от и ij, то получим уравнение f*( ij,T) = 0 поверхности текучести для идеальной упругопластической среды. При этом
(p) |
|
|
@f* |
|
@f* |
|
d"ij |
̸= 0, если f* = 0 |
и df* = |
|
d ij + |
|
dT = 0; |
@ ij |
@T |
|||||
d"(p) |
= 0, если f = 0 |
и df < 0 или f < 0. |
||||
ij |
* |
* |
|
* |
|
|
26 |
Модели термопластичности |
В общем случае упругопластической среды с упрочнением
при выполнении (3.4) возможны следующие процессы:
активное нагружение, если
df* = |
@f |
d ij + |
@f |
dT > 0, |
|
|||||
|
|
|
|
|
||||||
@ ij |
|
@T |
(3.5) |
|||||||
df = df* + |
@f |
|
d + |
|
@f |
d ij = 0, |
||||
|
|
|
||||||||
@ |
|
|
||||||||
|
|
|
|
@ ij |
|
|||||
и тогда d"ij(p) ̸= 0; |
|
|
|
|
|
|
||||
нейтральное нагружение, если |
|
|||||||||
|
df* = df = 0; |
|
||||||||
начало разгрузки, если |
|
|
|
|
|
|
||||
|
|
|
df* < 0. |
|
||||||
Для двух последних процессов d"ij(p) = 0. |
|
|||||||||
Введем параметр d * > 0, |
причем d * = 0, когда d"ij(p) |
= 0, |
||||||||
и представим внутренние параметры состояния в виде |
|
|||||||||
d = W( kl,T, kl, )d *, |
d ij = Wij( kl,T, kl, )d *. |
(3.6) |
||||||||
При активном нагружении из (3.5) и (3.6) получим
d * = |
− |
|
|
df* |
. |
||
W |
@f |
+Wij |
@f |
|
|||
|
@ |
@ |
|||||
|
|
|
|
ij |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда уравнение закона пластического течения можно записать в виде
d"ij(p) = Nij d +Yijkl d kl = Mij d *, |
(3.7) |
где, согласно (3.6),
Mij = NijW +YijklWkl,
Mij = Mji,
Mkk = 0.
Модели термопластичности |
27 |
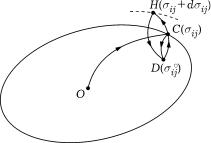
При построении некоторых вариантов ММ пластического деформирования используют постулат Драккера, обобщающий (1.2). Пусть тело, находящееся в исходном состоянии, нагружено по некоторому пути OC в пространстве напряжений (рис. 3.1), а затем из точки C, лежащей на поверхности нагружения и соответствующей значениям ij, разгружено до точки D, расположенной внутри этой поверхности и соответствующей значениям ij (в частном случае нейтрального нагружения точка D может находиться и на этой поверхности).
Рис. 3.1.
Если из точки D по пути DCH сначала перейти в точку C, а затем за счет приращений d ij провести активное нагружение до точки H, то на участке CH возникнут приращения d"(ije) ̸= 0
и d"(ijp) ̸= 0 компонент тензоров упругой и пластической деформации. Новое положение участка поверхности нагружения, на которой лежит точка H, отмечено на рис. 3.1 штриховой линией. После разгрузки по некоторому пути из точки H в точку D приходящаяся на единицу объема материала необратимая работа пластического деформирования составит
( ij − ij)d"(ijp) + d ij d"(ijp) > 0,
поскольку при замкнутом цикле нагружения работа, совершаемая напряжениями на упругих деформациях, равна нулю. Отсюда при ij = ij следует, что
d ij d"ij(p) > 0. |
(3.8) |
28 |
|
Модели термопластичности |
|
|
|
|||
Так как при |
= |
разность |
ij − |
может быть больше d |
ij |
, |
||
то |
ij ̸ |
ij |
|
ij |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
( ij − ij)d"ij(p) > 0. |
(3.9) |
||||
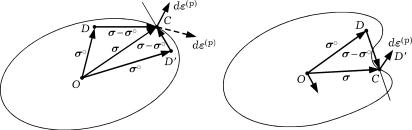
Неравенство (3.8) по аналогии со вторым условием (1.2) можно рассматривать как критерий устойчивости пластического деформирования при произвольном напряженном состоянии. Если в пространстве напряжений вдоль осей O ij откладывать компоненты "(ijp) с теми же индексами, то левую часть (3.9) можно интерпретировать как скалярное произведение векторов− и d"(p) соответственно с проекциями ij − ij и d"(ijp) на эти оси. Тогда (3.9) будет означать, что угол между этими векторами острый. Отсюда следует, что поверхность нагружения выпукла, а вектор d"(p) направлен по внешней нормали к этой поверхности (рис. 3.2, а). Действительно, так как положение точки D с координатами ij может быть выбрано произвольно относительно вектора (например, она может занимать положение D′), то при отклонении вектора d"(p) от направления нормали (штриховая линия со стрелкой на рис. 3.2, а) условие (3.9) может быть нарушено. При невыпуклой поверхности нагружения (рис. 3.2, б) независимо от направления вектора d"(p) всегда можно подобрать положение точки D, при котором будет нарушено условие (3.9).
а |
б |
Рис. 3.2.
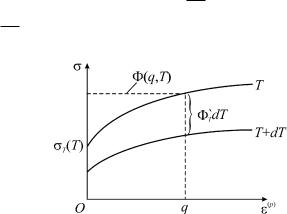
Пример 3.1. При неизотермическом деформировании в случае изотропного упрочнения соотношение (2.6) можно записать
Модели термопластичности |
29 |
в виде зависимости и = т( ,T), которая соответствует семейству диаграмм растяжения, перестроенных в координатах "(p), и (рис. 3.3). Тогда
|
d и = |
@ т |
|
d + |
@ т |
dT |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
@ |
|
|
|
|
@T |
|
|
||||||||
и, учитывая, что |
|
|
|
|
|
d"ij(p) |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
3 sij |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
, |
|
|
|
||||
|
|
|
|
|
|
2 и |
|
|
|
|||||||||||||
получаем |
|
|
|
|
|
d |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
sij |
|
d и − |
@ т |
dT |
, i,j = 1,2,3. |
||||||||||||||
d"(p) = |
|
@T |
||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
ij |
2 и |
|
|
|
@ т |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
@ |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
При и < т( ,T) материал деформируется упруго, если же спра- |
||||||||||||||||||||||
ведливо равенство и = |
|
т( ,T), то при d и > |
@ т |
dT происходит |
||||||||||||||||||
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
@T |
|
активное нагружение, при d и = @@Tт dT — нейтральное, а при d и < @@Tт dT начинается разгрузка.
Рис. 3.3.
#
Пример 3.2. Направляющие косинусы нормали к поверхности нагружения пропорциональны @f/@ij. Поэтому из коллинеарности этой нормали и вектора d"(p) следует равенство
(p) |
|
@f |
|
|
d"ij |
= |
|
d *, |
(3.10) |
@ij |

30 |
Модели термопластичности |
где лишь при активном нагружении коэффициент пропорциональности d * > 0, а в остальных случаях d * = 0. Сопоставляя (3.7) с равенством (3.10), выражающим ассоциированный с поверхностью нагружения закон пластического течения, получим, что
Mij d * = @f d *.
@ij
Так как функция f в (3.4) определена с точностью до произвольного множителя, то в (3.7) можно принять Mij = @f/@ij.
Если влияние внутренних параметров и ij на процесс пластического деформирования можно разделить и принять
f( ij,T, , ij) = fт( ij,T, ij) − т(T, ) = 0,
то вместо (3.7) получим
d"ij(p) = |
|
|
d kl + |
|
|
|
− |
|
|
dT |
|
@fт |
. |
||||
@ kl |
|
|
@T |
@T |
|||||||||||||
|
|
|
@fт( |
|
|
|
|
т |
|
|
|||||||
− |
@fт |
|
|
|
|
@fт |
|
@ |
т |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
@ij |
||||
|
|
Wkl @ |
kl |
− |
W |
|
@ |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
#
Пример 3.3. Пусть толстостенная труба внутренним радиусом a и внешним радиусом b изготовлена из изотропного материала и подвержена действию внутреннего давления p. Осесимметричное установившееся распределение T(r) температуры зависит лишь от радиальной координаты r [a, b], отсчитываемой от оси трубы, и его можно представить в виде
ln(b/r)
T(r) −T(b) = T(r) = #a ln(b/a), #a = T(a) −T(b). (3.11)
Положим, что T(b) является температурой естественного состояния материала трубы и при указанных условиях в нем возникает пластическая деформация. Если труба достаточно длинная, то можно считать, что имеет место плоское деформированное состояние, т. е. в направлении осевой координаты z деформация "zz = const. В дальнейшем примем "zz = 0.

Модели термопластичности |
31 |
Как при упругом, так и при пластическом деформировании материала трубы для ее любого поперечного сечения справедли-
во уравнение равновесия |
|
|
|
|
|
|
d rr |
+ |
rr − '' |
= 0, |
(3.12) |
|
dr |
r |
|||
|
|
|
|
||
где rr и '' — радиальное и окружное напряжения. При этом соответствующие компоненты тензора полной деформации равны
"rr = |
dur |
, |
"'' = |
ur |
, |
(3.13) |
|
dr |
r |
||||||
|
|
|
|
|
где ur — радиальное перемещение.
Пусть свойства материала трубы соответствуют свойствам идеальной упругопластической сплошной среды, подчиняющейся условию текучести (2.2), а также '' > zz > rr. Тогда (2.2)
примет вид |
f( ) = '' − rr = т, |
|
|
|||
|
|
|
предел |
|
(3.14) |
|
где |
т |
— |
̂ |
т |
, а также продоль- |
|
|
|
текучести. Положим, что |
||||
ный модуль упругости E, коэффициент Пуассона и температурный коэффициент линейного расширения (T) материала трубы не зависят от температуры.
Так как изменение объема происходит только вследствие упругой и температурной деформаций, то с учетом (3.13) имеем
dur |
+ |
ur |
= |
rr + '' + zz |
+ 3 (T) T(r). |
(3.15) |
|||||
|
dr |
r |
|
|
|||||||
|
|
|
|
3{ |
|
|
|
|
|||
Согласно (3.10) и (3.14) |
|
|
|
|
|
|
|||||
|
|
|
|
|
(p) |
@f( ) |
|
|
|
||
|
|
|
|
d"zz = |
|
̂ |
|
d * = 0. |
|
||
|
|
|
|
@ |
zz |
|
|||||
|
|
|
|
|
|
|
|
|
|
||
Поэтому в силу обобщенного закона Гука справедливо равенство
"zz = |
zz − ( rr + '') |
+ (T) T(r) = 0. |
(3.16) |
|
E |
||||
|
|
|
Выражая отсюда zz, подставляя его в (3.15) и учитывая (3.12), после интегрирования получаем
ur = |
(1 − 2 )(1 + ) |
r rr + |
2(1 + ) (T) |
|
r |
||
|
E |
||
b
∫ T(r)r dr + Cr0 . (3.17)
a

32 Модели термопластичности
Соотношение (3.17) справедливо как в области упругой деформации, так и в области пластической деформации.
Если из равенств
|
du |
|
|
rr |
|
( '' + |
zz |
) |
|
|
|
|
||||
"rr = |
|
r |
= |
|
− |
|
|
|
+ (T) T(r), |
|
||||||
dr |
|
|
|
E |
|
|
|
(3.18) |
||||||||
|
ur |
|
'' |
|
( rr + zz) |
|
|
(T) |
|
|
|
|||||
"'' = |
|
|
= |
|
|
− |
|
|
|
+ |
|
T(r) |
|
|
||
r |
|
|
|
E |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
для обобщенного закона Гука исключить ur и использовать выражения для '' из (3.12) и для zz из (3.16), то получим
|
|
|
d2 rr |
|
3 d rr |
|
|
|
|
E (T) |
|
d T |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
= 0 |
|
|
|
||||||
|
|
|
|
dr2 |
r dr |
r(1 − ) |
|
|
dr |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
и после интегрирования, учитывая (3.11), найдем |
|
|
|
||||||||||||||||||||||||||||||
C1 |
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
E (T)#a |
|
|
|
|
|
||||||||||||
rr = |
|
|
+ C2 − ln |
|
, |
|
|
= |
|
|
|
|
|
|
|
|
|
|
. |
(3.19) |
|||||||||||||
r |
2 |
|
|
|
2(1 |
− |
)ln( |
b |
/ |
a |
) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Из (3.12) и (3.14) получим условие |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
r ddrrr r=r0 = т, |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
которому должна удовлетворять |
|
граница r = r0 области упругой |
|||||||||||||||||||||||||||||||
деформации, что позволяет в (3.19) записать |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2C1 |
= − т. |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
r2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким образом, согласно (3.19) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
d rr |
|
|
|
|
|
|
|
|
|
|
|
|
r2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
r |
|
|
|
|
|
|
= ( |
т − |
) |
0 |
+ . |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
dr |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r2 |
|
|
|
|
|
|
|
|
|
|
||||||||
Отсюда следует, что при т = условие текучести будет выполнено во всем поперечном сечении трубы, что соответствует неустойчивому пластическому течению материала трубы. Если т > , то область упругой деформации занимает внешнюю часть поперечного сечения трубы при r > r0, поскольку

Модели термопластичности |
33 |
при углублении в эту область величина r d rr/dr должна убывать. Отметим, что это неравенство заведомо справедливо, когда
#a < 0, т. е. температура T(a) внутренней поверхности трубы ниже температуры T(b) наружной поверхности.
При т > , согласно граничному условию rr(b) = 0, из (3.19) найдем
|
|
|
|
|
|
|
|
|
|
|
|
C1 |
|
|
|
|
|
( |
− |
т)r |
2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
C2 |
= |
|
|
|
= |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
−b2 |
|
|
|
|
|
2b2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
и в итоге при r [r0, b] получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
т |
|
r2 |
|
|
|
r2 |
|
|
|
|
|
|
|
b |
|
|
|
|||||||||||
|
|
|
rr |
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
− |
|
)− |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
2 |
|
|
|
r2 |
b2 |
|
|
|
r |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
= |
|
|
− |
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
ln |
|
|
, |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
далее из (3.12) следует |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
= |
т − |
|
|
|
|
|
r02 |
+ |
r02 |
|
|
|
+ |
|
1 |
− |
ln |
b |
, |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
'' |
|
|
|
2 |
|
|
|
· (r2 |
|
b2 ) |
|
( |
|
|
|
r ) |
|||||||||||||||||||||
а затем из (3.16) — |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
||
|
zz = ( т − )b2 + ( − |
2ln r ). |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Приравнивая при |
|
r = b |
|
|
значения |
|
ur |
из |
|
|
(3.17) |
и из второго |
||||||||||||||||||||||||||
уравнения (3.18), находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
(1 |
− |
2)( т |
|
− |
)r2 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
C0 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
. |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для области пластической деформации из условия
r ddrrr = т
при r [a, r0] путем интегрирования (с учетом непрерывностиrr при r = r0) имеем
|
|
= |
ln |
r |
− |
|
ln |
b |
− |
т − |
( |
1 |
− |
|
r0 |
r0 |
2 |
||||||||||
|
rr |
т |
|
|
|
|
Из граничного условия
rr(a) = −p
r2 )
b02 . (3.20)

34 |
|
|
Модели термопластичности |
||||||||||||
с учетом (3.20) получим уравнение |
|
|
|
|
|
||||||||||
|
|
ln |
a |
+ |
|
= |
|
ln |
b |
+ |
т − |
1 |
|
r02 |
|
|
|
p |
|
|
2 |
− b2 ) |
|||||||||
|
т |
|
r0 |
|
|
r0 |
( |
||||||||
относительно r0. Если в трубе сначала возникло установившееся распределение температуры, которое не вызвало пластических деформаций, а затем стало возрастать давление, то из последнего уравнения при r0 = a следует, что пластическая деформация возникнет при значении давления
p* |
= |
ln |
b |
+ |
т − |
1 |
|
r02 |
. |
|
2 |
|
|||||||
|
r0 |
( |
− b2 ) |
||||||
Случай p* < 0 означает, что пластические деформации возникают еще до повышения давления.
Используя (3.20), в области пластической деформации можно сначала найти '' из (3.14), а затем zz — из (3.16).
Вопросы и задачи
1.Что называют термопластичностью?
2.Что называют тензором микронапряжений?
3.Напишите соотношения, характеризующие активное нагружение, нейтральное нагружение, разгрузку.
4.Напишите закон пластического течения.
5.Сформулируйте постулат Драккера.
6.Напишите соотношение, выражающее ассоциированный закон пластического течения.
7.Что такое неустойчивое пластическое течение? Приведите пример.
