3.7. Итерация поиска по методу Хука—Дживса в примере 3.3.

¹⁾ Методы Розенброка и Дэвиса, Свенна, Кемпи более подробно изложены в книге Химмельблау [69], переведенной на русский язык,— Прим. Перев

Вместе с тем вопрос о том, являются ли дополнительные усложнения метода Хука — Дживса оправданными, по-видимому, остается открытым. Если же существует возможность реализовать более сложный алгоритм, то предпочтение следует отдать методу Пауэлла, превосходство которого над рассмотренными выше эвристическими методами несомненно.

3.2.3. Метод сопряженных направлений Пауэлла

Наиболее эффективным из алгоритмов прямого поиска является метод, разработанный Пауэллом [15], в особенности его модифици­рованные варианты, предложенные Зангвиллом [16] и Брентой [17]. При работе этого алгоритма информация, полученная на предыдущих итерациях, используется для построения векторов направлений поиска, а также для устранения зацикливания последовательности координатных поисков. Метод ориентирован на решение задач с квадратичными целевыми функциями и основывается на фундаментальных теоретических результатах.

Задачи с квадратичными целевыми функциями занимают важное место в теории оптимизации по двум причинам.

1. Квадратичная функция представляет простейший тип нелинейных функций, для которых может быть сформулирована задача безусловной оптимизации (линейные функции не обладают внутренними оптимумами). Следовательно, если с помощью того или иного метода успешно решаются задачи оптимизации с целевыми функциями общего вида, то такой метод должен оказаться эффективным при решении задач с квадратичными функциями.

2. В окрестности точки оптимума любую нелинейную функцию можно аппроксимировать квадратичной функцией (поскольку линейный член разложения Тейлора обращается в нуль). Следовательно, работа алгоритма при решении задач с квадратичными функциями позволяет получить определенное представление о сходимости алгоритма в случае, когда минимизируется функция общего вида.

Основная идея алгоритма заключается в том, что если квадратичная функция N переменных приведена к виду суммы полных квадратов, то ее оптимум может быть найден в результате реализации N одномерных поисков по преобразованным координатным на­правлениям.

Процедура преобразования квадратичной функции

q(x) = a + bx + ½ xCx (3.25)

к виду суммы полных .квадратов эквивалентна нахождению такой матрицы преобразования Т, которая приводит матрицу квадратич­ной формы к диагональному виду. Таким образом, заданная квадратичная форма

Q(x) = xCx (3.26)

путем преобразования

x = Tz (3.27)

приводится к виду

Q(x) = zTCTz = zDz (3.28)

где D — диагональная матрица, т. е. элементы D отличны от нуля только при i = j

f(x) = 4x+ 3x- 4xx+ x

Рис. 3.8. Линии уровня квадратичной функции с перекрёстными членами.

Пусть t — j-й столбец матрицы Т. Тогда преобразование (3.27) позволяет записать каждый вектор х в виде линейной комбинации вектор-столбцов t.

x = Tz = tz+ tz+…+ tz . (3.29)

Другими словами, вместо координат вектора х в стандартной коор­динатной системе, определяемой множеством векторов e⁽ⁱ⁾, используются координаты вектора в новой координатной системе, заданной векторами t. Кроме того, система векторов t соответствует главным осям рассматриваемой квадратичной формы, поскольку матрица квадратичной формы приводится к диагональному виду. Такая ситуация возникает, если квадратичную функцию с перекрестными членами, линии уровня которой изображены на рис. 3.8, записать в новой координатной системе, оси которой совпадают с большой и малой осями квадратичной функции (см. рис. 3.9).

Итак, с помощью преобразования переменных квадратичной функции строится новая система координат, совпадающих с главными осями квадратичной функции. Следовательно, одномерный поиск точки оптимума в пространстве преобразованных переменных z эквивалентен поиску вдоль каждой из главных осей квадратичной функции. Так как направления главных осей определяются векторами t одномерный поиск проводится в направлениях, заданных этими векторами. Проиллюстрируем вышеизложенное примером.

f(x) = 4x+ 2x+ x+x

Рис. 3.9. Линии уровня квадратичной функции без перекрёстных членов

Пример 3.4. Преобразование к виду суммы квадратов

Рассмотрим функцию

f(x) = 4x+ 3x– 4xx+ x

и преобразование

x= z+ ½ z, x= z,

или

Преобразованная квадратичная функция принимает следующий вид:

f(z)= 4z+ 2z+ z+ ½ z.

Заметим, что это преобразование не является единственным, поскольку система векторов t не удовлетворяет условию ортонормированности. В частности, нетрудно проверить, что преобразование

также приводит матрицу квадратичной формы к диагональному, виду. Задавая начальную точку x= [0, 0]и два столбца матрицы преобразования

t= [1, 0], t= [½, 1],

можно найти точку оптимума [–,–]^T в результате проведения двух последовательных поисков в направлениях t и t Поиск в направлении t по формуле

x= x+ λt

позволяет получить значение λ = – и точку х⁽¹⁾ = [–, 0]. Далее из точки х⁽¹⁾ проводится поиск в направлении t₂. Получаем значение λ = – и решение х⁽²⁾ = [–,–]^T.

Из рассмотренного примера и предыдущего изложения следует, что если система векторов t, j = 1,...,N, или система сопряженных направлений, построена, то точку оптимума квадратичной функции можно найти в результате реализации в точности N одномерных поисков, которые проводятся вдоль каждого из N направлений t, j = 1,...,N. Таким образом, нерешенными остаются лишь вопросы, связанные с построением системы векторов t. Если матрица С известна, то матрицу преобразования Т можно найти с помощью метода Гаусса — Жордана (как это выполнено в приложении А). Метод Гаусса — Жордана позволяет представить матрицу С в виде произведения

C = P^TDP, откуда (3.30)

(P)C(P) = D и T = P (3.31)

Однако матрица С (или ее оценка) в данном случае неизвестна, по­скольку речь идет о построении метода решения задач безусловной оптимизации с целевой функцией f(x), при реализации которого используются только значения функции и не используются значе­ния первых и тем более вторых производных. Тем не менее и в этом случае можно определить систему сопряженных направлений на основе следующего элементарного свойства квадратичных функ­ций.

Свойство параллельного подпространства

Пусть заданы квадратичная функция q(x), две произвольные не­совпадающие точки x⁽¹⁾ и х⁽²⁾, а также направление d. Если точка y⁽¹⁾ минимизирует q(x⁽¹⁾+λd), a точка y⁽²⁾ минимизирует q(x⁽¹⁾+ λd), то направление (y⁽²⁾ - y⁽¹⁾) сопряжено с d.

Рис. 3.10 иллюстрирует сформулированное свойство для случая двух переменных. Нетрудно видеть, что поиск, проводимый из точки y⁽¹⁾ или y⁽²⁾ в направлении (y⁽²⁾ - y⁽¹⁾), обеспечивает получение точки минимума. Таким образом, в случае двух переменных реализация трех одномерных поисков позволяет построить систему сопряженных направлений и, кроме того, найти точку оптимума квадратичной функции. Прежде чем продолжать алгоритмические построения, докажем теорему о свойстве параллельного подпространства.

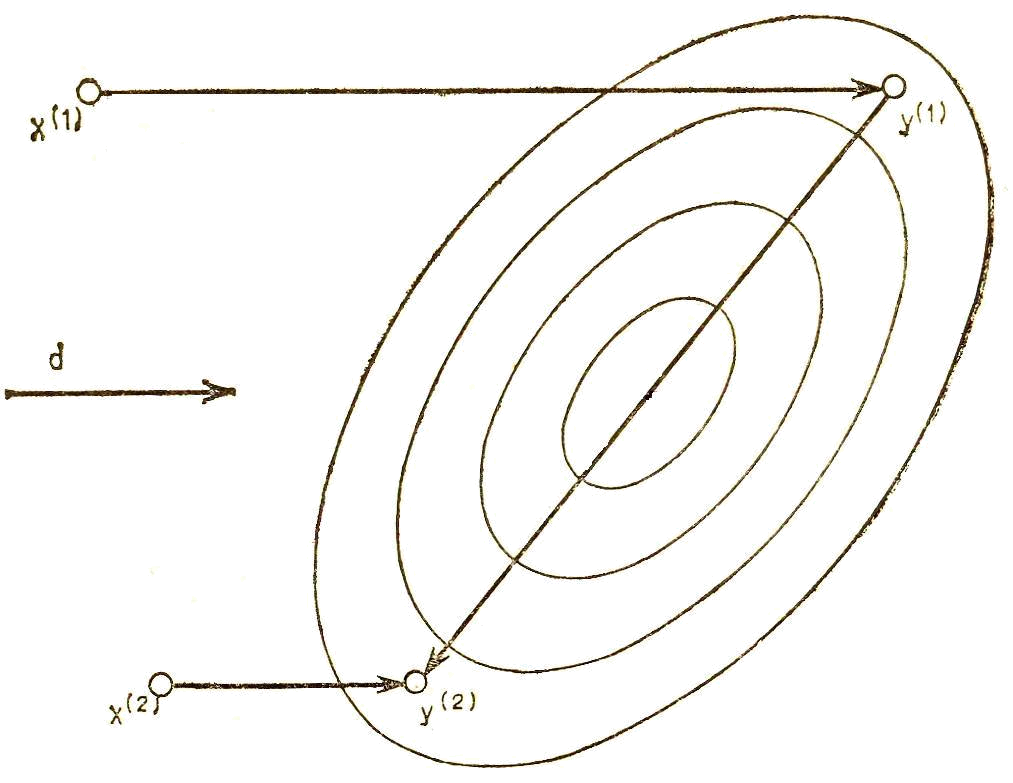
Рис. 3.10. Сопряженные направления на плоскости.

Напомним, что по определению С-сопряженные направления задаются системой вектор-столбцов матрицы Т, которая приводит матрицу С к диагональному виду:

ТCТ = D (3.32)

Поскольку все внедиагональные элементы D равны нулю, отсюда следует, что

(3.33)

где t — i-й столбец матрицы Т. Таким образом, мы получили возможность дать более удобное, эквивалентное и, по-видимому, более конструктивное определение сопряженности направлений.

Сопряженные направления

Пусть С — симметрическая матрица порядка NN; направления s⁽¹⁾, s⁽²⁾, s⁽³⁾,..., s, r ≤ N, называются С-сопряженными, если эти направления линейно независимы и

sCs= для всех i ≠ j. (3.34)

Опять обратимся к квадратичной функции общего вида

q(x) = a + b^Tx+(¹/_t)x^TCx.

Точки прямой, исходящей из х⁽¹⁾ в направлении d, задаются формулой

x = x+λd.

Минимум q(x) вдоль направления d определяется путем нахождения значения λ*, при котором q/λ=0. Вычислим эту производную по правилу дифференцирования сложной функции:

= =b+ xCd. (3.35)

По предположению теоремы минимум достигается в точке y⁽¹⁾ следовательно,

[(y⁽¹⁾ )C b ] d = 0. (3.36)

Аналогично, так как минимум q(x) при движении из точки х⁽²⁾ в направлении d достигается в точке y⁽²⁾ имеем

[(y⁽²⁾ )C b ] d = 0. (3.37)

Вычитая (3.36) из (3.37), получаем

(y⁽²⁾ - y⁽¹⁾ )Cd = 0 (3.38)

В соответствии с данным выше определением направления d и (y⁽²⁾ - y⁽¹⁾ ) оказываются С-сопряженными, и свойство параллельного подпространства для квадратичных функций доказано.

Пример 3.5. Минимизация на основе свойства параллельного подпространства.

Опять рассмотрим квадратичную функцию q(x) = 4x+ 3x - 4xx+ x. Пусть заданы две точки х⁽¹⁾ = [0, 0],х⁽²⁾ = [1,0]и направлениеd = [l, 1]^T. Первый поиск проводится вдоль прямой

x = [0, 0]+λ [1, 1]

и приводит к точке y⁽¹⁾ = [-,-](λ*= -). Второй поиск проводится вдоль прямой

x = [1, 0]+λ [1, 1]

и позволяет получить точку y⁽²⁾ = [,–](λ*=–). Согласно свойству параллельного подпространства, направление

y⁽²⁾ – y⁽¹⁾ = [,–]– [–,–]= [,–]

сопряжено с d = [l, 1]^T

[l, 1]C[,–].

Выше отмечалось, что в случае двух переменных оптимум q(x) можно найти путем проведения поиска вдоль прямой, заданной направлением (y⁽²⁾ – y⁽¹⁾ ). Этот факт нетрудно проверить, поскольку минимум q(x) вдоль прямой

x = [–,–]+λ [,–]

достигается в точке х* = [–,–]^T(λ* = –), которая сов­падает с полученным ранее решением.

В рассмотренных выше построениях для того, чтобы определить сопряженное направление, требовалось задать две точки и некоторое направление. Это не слишком удобно при проведении расчетов, поэтому предпочтительнее строить систему сопряженных направлений, исходя из одной начальной точки, что легко осуществить при помощи единичных координатных векторов е⁽¹⁾, е⁽²⁾, е⁽³⁾,..., е^(N). (Здесь рассматривается процедура построения сопряженных на­правлений в случае двух переменных, которая допускает очевидное обобщение для N-мерного пространства.) Пусть е⁽¹⁾ = [l, 0]ие⁽²⁾ = [0, 1]. При заданной начальной точкех⁽⁰⁾ вычислим значение λ⁽⁰⁾, которому соответствует минимум f (х⁽⁰⁾ + λ⁽⁰⁾ е⁽¹⁾).

Положим

x⁽¹⁾ = х⁽⁰⁾ + λ⁽⁰⁾ е⁽¹⁾.

и вычислим значение λ⁽¹⁾, которому соответствует минимум f (х⁽¹⁾ + λ⁽¹⁾ е⁽²⁾). Положим

x⁽²⁾ = х⁽¹⁾ + λ⁽¹⁾ е⁽²⁾.

Далее вычислим значение λ⁽²⁾, минимизирующее f (х⁽²⁾ + λ⁽²⁾ е⁽¹⁾), и положим

x⁽³⁾ = х⁽²⁾ + λ⁽²⁾ е⁽¹⁾.

При этом направления (х⁽³⁾ – х⁽¹⁾) и е⁽¹⁾ оказываются сопряженными. Для того чтобы убедиться в этом, рассмотрим рис. 3.11. Заметим, что точка х⁽¹⁾ найдена в результате поиска из точки х⁽⁰⁾ в направление е⁽¹⁾, а точка х⁽³⁾ получена при поиске из точки х⁽²⁾ в направлении е⁽¹⁾. Следовательно, направление е⁽¹⁾ и (х⁽³⁾ – х⁽¹⁾) являются сопряжёнными согласно свойству параллельного подпространства. Далее если на следующей итерации провести поиск в направлении (x⁽³⁾ – x⁽¹⁾), то процедура поиска будет охватывать два сопряженных направления, и поскольку f(x) предполагается квадратичной функцией двух переменных, в результате будет найдено решение х*.

Проведенное на основе свойства параллельного подпространства построение рассмотрено для случая, когда число сопряженных направлений равняется двум. Однако это построение естественным образом обобщается на случай задач более высокой размерности

В частности, нетрудно показать, что если точка y⁽¹⁾ найдена в результате поиска из точки х⁽¹⁾ вдоль каждого из М (<N) сопряженных направлений, а точка y⁽²⁾ получена в результате поиска из точки х⁽²⁾ вдоль каждого из тех же М сопряженных направлений s⁽¹⁾, s⁽²⁾, s⁽³⁾,..., s^(M) то вектор (y⁽²⁾ – y⁽¹⁾) задает направление, сопряженное со всеми выбранными М направлениями. Это утверждение известно как обобщенное свойство параллельного подпространства. Используя указанное свойство, можно обобщить метод построения сопряженных направлений, последовательные шаги реализации которого отражены на рис. 3.11 на случай пространства управляемых переменных более высокой размерности. Рис. 3.12 иллюстрирует построение сопряженных направлений в трехмерном пространстве.

Как показано на рис. 3.12, сначала поиск осуществляется вдоль трех координатных направлений е⁽¹⁾, е⁽²⁾ и е⁽³⁾ затем эти направления последовательно заменяются вновь построенными сопряженными направлениями. Серия одномерных поисков из точки x⁽⁰⁾ проводится в направлении е⁽³⁾, затем е⁽¹⁾, е⁽²⁾ и снова е⁽³⁾; в результате построены сопряженные направления е⁽³⁾ и (x⁽⁴⁾ – x⁽¹⁾). Направление е⁽¹⁾ заменяется новым направлением поиска, которое на рис. 3.12 обозначено цифрой 4. Следующая серия поисков проводится в направлении 4, затем е⁽²⁾, е⁽³⁾ и снова 4. Согласно обобщенному свойству параллельного подпространства, новое направление (x⁽⁸⁾ – x⁽⁵⁾), обозначенное на рисунке цифрой 5, сопряжено не только с 4, но и с е⁽³⁾. Следовательно, направления е⁽³⁾, (x⁽⁴⁾ – x⁽¹⁾) и (x⁽⁸⁾ – x⁽⁵⁾) образуют систему взаимно сопряженных направлений.

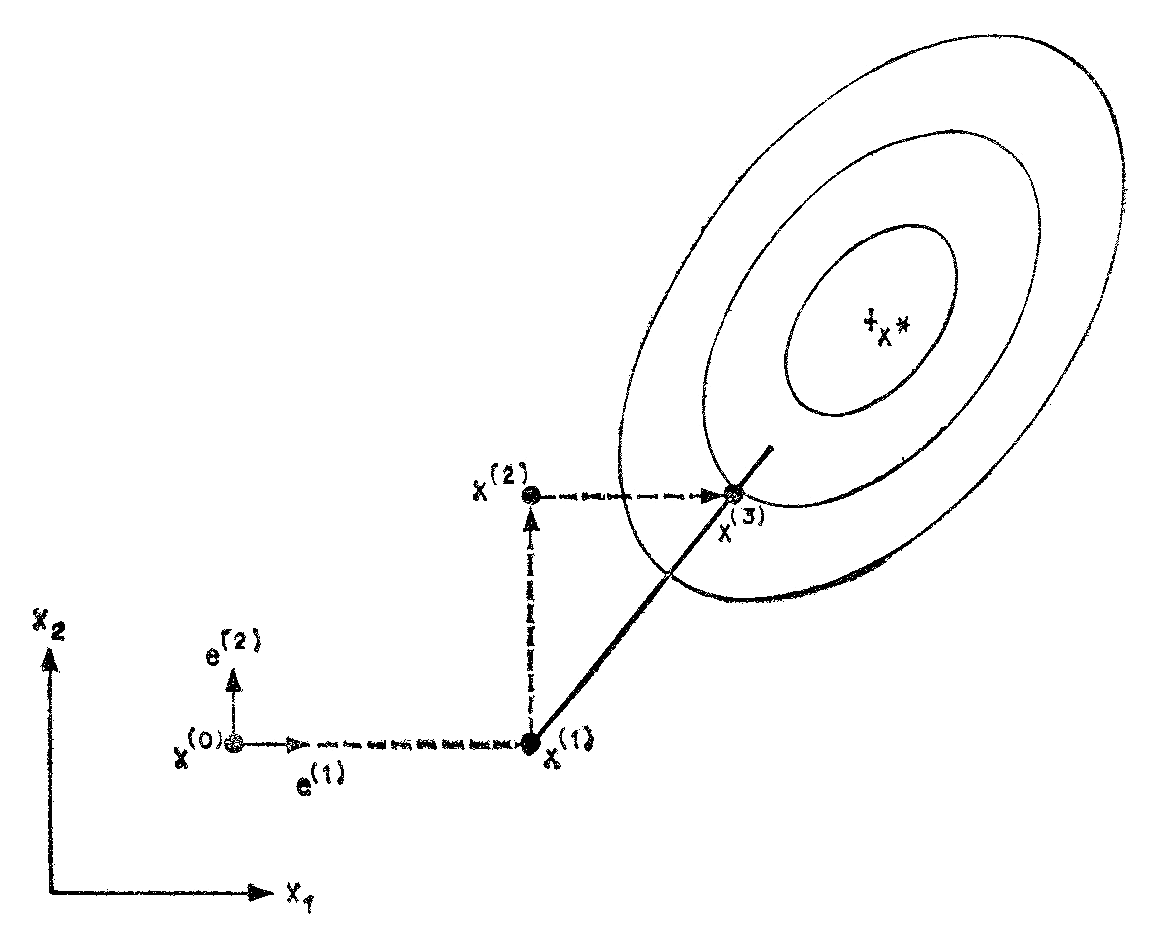
Рис. 3.11. Построение сопряженных направлений из одной точки.

Поэтому если провести дополнительный поиск из точки x⁽⁵⁾ в направлении (x⁽⁸⁾ – x⁽⁵⁾) (т. е. в направлении 5 на рисунке), то будет найдена точка x⁽⁹⁾, в которой должен достигаться оптимум квадратичной функции трех переменных f(x), поскольку поиск последовательно осуществляется в трех взаимно сопряженных направлениях. Таким образом, в трехмерном случае для нахождения точного (если, разумеется, оперировать недесятичными дробями) оптимума квадратичной функции требуется провести девять поисков вдоль прямой с использованием только значений функции. Алгоритм легко обобщается и в случае N-мерного пространства требует проведения последовательности N одномерных поисков, которая приводит к получению точки оптимума квадратичной функции. Ниже представлены шаги обобщенного алгоритма.

Рис. 3.12. Построение сопряженных направлений в трехмерном пространстве.

Метод сопряженных направлений Пауэлла

Шаг 1. Задать начальную точку х⁽⁰⁾ и систему N линейно независимых направлений; возможен случай, когда s⁽ⁱ⁾ = e⁽ⁱ⁾ i = 1, 2, 3,..., N.

Шаг 2. Минимизировать f(x) при последовательном движении по (N+1) направлениям; при этом полученная ранее точка минимума берется в качестве исходной, а направление s^(N) используется как при первом, так и последнем поиске.

Шаг 3. Определить новое сопряженное направление с помощью обобщенного свойства параллельного подпространства.

Ш а г 4. Заменить s^(l) на s⁽²⁾ и т. д. Заменить s^(N) сопряженным направлением. Перейти к шагу 2.

Для того чтобы применить изложенный метод на практике, его необходимо дополнить процедурами проверки сходимости и линей­ной независимости системы направлений. Проверка линейной неза­висимости особенно важна в тех случаях, когда функция f(x) не является квадратичной [16, 17].

Из способа построения алгоритма следует, что в случае, когда целевая функция квадратична и обладает минимумом, точка минимума находится в результате реализации N циклов, включающих шаги 2, 3 и 4, где N — количество переменных. Если же функция не является квадратичной, то требуется более чем N циклов. Вместе с тем можно дать строгое доказательство того, что при некотором предположении метод Пауэлла сходится к точке локального мини­мума с суперлинейной скоростью (см. данное ниже определение).

Скорость сходимости. Рассматриваемый метод позволяет построить последовательность точек х^(k), которая сходится к решению x*. Метод называется сходящимся, если неравенство

≤1, где (3.39)

= x– х*, (3.40)

выполняется на каждой итерации. Поскольку при расчетах обычно оперируют конечными десятичными дробями, даже самый эффективный алгоритм требует проведения бесконечной последовательности итераций. Поэтому в первую очередь интерес представляют асимпто­тические свойства сходимости изучаемых методов. Будем говорить, что алгоритм обладает сходимостью порядка r (см. [18, 19]), если

, (3.41)

где С — постоянная величина. Из формулы (3.39) следует, что при r = 1 имеет место неравенство С ≤ 1. Если r = 1 или r = 2, то алгоритм характеризуется линейной или квадратичной скоростью сходимости соответственно. При r = 1 и С = 0 алгоритм характеризуется суперлинейной скоростью сходимости.

Пример 3.6. Метод сопряженных направлений Пауэлла

Найти точку минимума функции

f(x) = 2x+ 4xx – 10xx+ x,

если задана начальная точка х⁽⁰⁾ = [5, 2]^T, в которой f (x⁽⁰⁾) = 314.

Шаг 1. s⁽¹⁾ = [l, 0]^T, s⁽²⁾ = [0, 1]^T.

Шаг 2. (а) Найдем такое значение λ, при котором

f (x⁽⁰⁾ + λs⁽²⁾) → min.

Получим: λ* -0,81, откуда

x^(l) = [5, 2]^T - 0,81 [0, 1]^T = [5, 1.19]^T, f (x^(l)) = 250.

(б) Найдем такое значение λ, при котором f (x⁽¹⁾ + λs⁽¹⁾) → min.

λ* = –3,26, x⁽²⁾ = [1.74, 1.19]^T, f (x⁽²⁾) = 1.10.

(в) Найдем такое значение λ, при котором f (x⁽²⁾ + λs⁽²⁾) → min.

λ* = –0.098, x⁽³⁾ = [1.74, 1.092]^T, f (x⁽³⁾) = 0.72.

Шаг 3. Положим s⁽³⁾ = х⁽³⁾ - x⁽¹⁾ = [-3.26,-0.098]^T. После нормировки получим

s⁽³⁾ = = [–0,99955, –0,03]^T.

Положим s⁽¹⁾ = s⁽²⁾, s⁽²⁾ = s⁽³⁾ и перейдем к шагу 2 алгоритма.

Шаг 4. Найдем такое значение λ, при котором f (x⁽³⁾ + λs⁽²⁾) → min.

λ* = –0.734, x⁽⁴⁾ = [1.006, 1.070]^T, f (x⁽⁴⁾) = –2,86.

Примечание. Если бы f(x) была квадратичной функцией, то полученная точка являлась бы решением задачи (если пренебречь ошибкой округления). В данном случае итерации следует продолжить до получения решения.

Направления поиска, полученные в процессе реализации метода, показаны на рис. 3.13.

Результаты вычислительных экспериментов позволяют утверж­дать, что метод Пауэлла (дополненный процедурой проверки линейной зависимости направлений) отличается по меньшей мере столь же высокой надежностью, как и другие методы прямого поиска, и в ряде случаев является значительно более эффективным. Поэтому проблема выбора алгоритма прямого поиска часто (и обоснованно) разрешается в пользу метода Пауэлла.

Здесь заканчивается рассмотрение методов прямого поиска решений в задачах безусловной оптимизации. В следующем разделе описываются методы, основанные на использовании производных.