3.4. Сравнение методов и результаты вычислительных экспериментов

Исследования, проведенные в последние годы, позволили на теоретической основе рассмотреть сходимость методов, изложенных в предыдущих разделах. Вместе с тем значительная часть сведений об эффективности применения указанных методов к задачам с целевыми функциями общего вида получена в результате проведения вычислительных экспериментов. Очень часто изложение нового метода в той или иной публикации сопровождается кратким сравнительным обзором результатов соответствующих вычислений. В ряде случаев тестовые задачи выбираются таким образом, чтобы подчеркнуть положительные характеристики нового метода. Этот способ представления материала несколько ограничивает степень обоснованности публикуемых результатов.

Химмельблау (см. [69, гл. 5]) приводит численные результаты реализации ряда методов. Полученные им данные представляют значительный интерес, поскольку Химмельблау не является сторонником того или иного метода. Он характеризует каждый метод (прямого поиска или градиентный) в соответствии с его устойчивостью, количеством требуемых вычислений значений функции и количеством необходимого для реализации алгоритма машинного времени при решении ряда тестовых задач. Устойчивость метода отражает успех в получении оптимального решения с заданной точностью для широкого круга задач. Химмельблау делает вывод, что методы Бройдена — Флетчера — Шэнно, Дэвидона — Флетчера — Пауэлла и метод прямого поиска Пауэлла лучше остальных методов. Более подробные сведения можно найти в книге Химмельблау.

Аналогичное, но менее полное исследование выполнено Сарджентом и Себастьяном в работе [70], где приведены результаты применения градиентных методов, в том числе алгоритмов Бройдена — Флетчера — Шэнно, Дэвидона — Флетчера — Пауэлла и Флетчера — Ривса. Они изучали влияние параметра сходимости для одномерного поиска, частоты возвратов к начальной итерации, положительной определенности матрицы Гессе для квазиньютоновских методов и точности вычисления компонент градиента. Полученные ими результаты указывают на превосходство квазиньютоновских методов (в частности, метода. Бройдена — Флетчера — Шэнно) при решении задач с функциями общего вида. Сарджент и Себастьян отмечают также, что точность расчетов на ЭВМ оказывает более заметное влияние на реализацию квазиньютоновских методов, чем на реализацию методов сопряженных градиентов. Это позволяет сделать вывод о том, что при расчетах на микро-ЭВМ (подобных тем, которые иногда используются в управлении технологическими процессами) метод Флетчера — Ривса может оказаться наиболее эффективным.

Карпентер и Смит [71] исследовали относительную эффективность вычислений по методу Ньютона для задач специальной структуры. Они сделали вывод, что для рассматриваемого круга задач методы Дэвидона — Флетчера — Пауэлла и метод Ньютона обладают преимуществом перед методом прямого поиска Пауэлла, а метод Дэвидона — Флетчера — Пауэлла превосходит метод Ньютона при решении задач большой размерности. Несколько позже Шэнно и Фуа [40, 56, 57] провели подробный анализ методов сопряженных градиентов и переменной метрики на основе вычислительных экспериментов. Полученные ими результаты весьма затруднительно изложить в краткой форме (читателю следует обратиться к указанным выше работам); однако можно отметить, что результаты указывают на преимущество метода Бройдена — Флетчера — Шэнно перед остальными методами.

Здесь, по-видимому, нецелесообразно уделять значительное внимание теоретическим вопросам проведения вычислительных экспериментов. С другой стороны, необходимо упомянуть о наличии определенных правил проверки алгоритмов [72], а также отметить, что числовые результаты, представленные в литературе примерно до 1977 г., следует использовать с известной осторожностью. Оценки эффективности тех или иных алгоритмов, полученные на основе анализа только количества вычислений значений функции, могут привести к неверным выводам, что подчеркивалось в работе Миля и Гонсалеса [73].

Авторы данной книги провели ряд вычислительных экспериментов для того, чтобы продемонстрировать относительные возможности реализации методов Коши, Флетчера — Ривса, Дэвидона — Флетчера — Пауэлла и Бройдена — Флетчера — Шэнно на ЭВМ CDC-6500 с обычной точностью. Возврат к начальной итерации по методу Флетчера — Ривса осуществлялся после каждой серии из N +1 шагов; критерии окончания поиска представлены в табл. 3.2.

Таблица 3.2. Критерии окончания поиска

1.k > M 3. ≤ ε

2. ≤ ε4.f (x)s(x) ≥ 0

5.f (x) > f (x)

В табл. 3.3 приведены результаты исследования функции Розен-брока (рис. 3.16):

f (x) = 100(x–x)+ (1 –x), (3.92)

которая обычно используется при анализе градиентных методов. Результаты получены с помощью различных методов поиска вдоль прямой; во всех случаях применялась процедура численной аппрок­симации градиента. Заметим, что комбинация «метод Коши/метод деления интервала пополам» обеспечивает нахождение наиболее точного значения f, однако при этом требуются наибольшие затраты машинного времени. Самым эффективным по количеству вычислений значений функции оказывается метод Бройдена — Флетчера — Шэнно с использованием кубичной аппроксимации. Отметим, что метод Коггинса представляет собой один из вариантов метода квадратичной интерполяции [21].

Табл. 3.4 содержит результаты анализа задачи, связанной с минимизацией инерции зубчатой передачи [74]. Эта задача (рис. 3.17) была включена Изоном и Фентоном в число тестовых задач для сравнения различных алгоритмов. Ее целевая функция записывается в следующем виде:

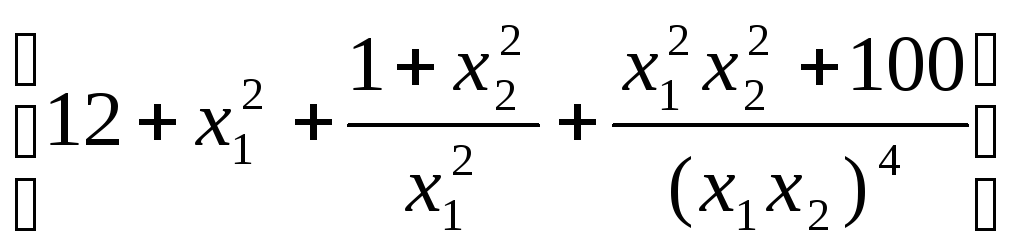
f(x) = . (3.93)

f (x) = 100(x–x)+ (1 –x)

Рис. 3.16. Линии уровня функции Розенброка.

Отметим, что в данном случае алгоритм Флетчера — Ривса с использованием кубической аппроксимации является наиболее эффективным как по затратам машинного времени, так и по количеству вычислений значений функции.

В табл. 3.5 приведены результаты исследования функции Вуда [75] (рис.3.18):

f (x) = 100(x–x)+ (1 –x)+ 90(x– x)+ (1–x)+ 10.1[(x– 1)+ (x– 1)]+

+19.8(x– 1)(x– 1). (3.94)

Опять комбинация метода Флетчера — Ривса с методом кубичной аппроксимации оказывается наиболее эффективной. Следует отметить, что представленные в этом разделе данные не в полной мере согласуются с другими опубликованными результатами. В первую очередь это касается метода Флетчера — Ривса, результаты реализации которого оказались значительно лучше результатов, полученных другими авторами. По-видимому, окончательные выводы можно будет сделать только после проведения дополнительных вычислительных экспериментов.

Таблица 3.3. Результаты исследования функции Розенброка (х⁽⁰⁾ = [–1.2, 1.0])

Метод	Метод
	деления интервала пополам	золотого сечения	Коггинса	кубической апроксимации
Коши	1.10E-10 / 7.47 / 38424а)	1.25E-10 / 1.382 / 4066	8.30E-8 / 1.074 / 3570	6.19E-9 / 2.631 / 10685
Флетчера — Ривса	3.24E-6 / 0.18 / 988	5.91E-6 / 0.57 / 805	5.96E-5 / 0.109 / 370	2.77E-7 / 0.059 / 273
Дэвидона — Флетчера — Пауэлла	2.45E-8 / 0.173 / 977	2.39E-8 / 0.133 / 656	6.6E-8 / 0.115 / 331	4.3E-8 / 0.063 / 239
Бройдена — Флетчера — Шэнно	5.6E-8 / 0.169 / 932	3.6E-8 / 0.161 / 740	2.1E-8 / 0.115 /315	3.9E-9 / 0.065 / 204

^а) f (x*) / время / К.Ф., где К.Ф. количество вычислений значений функции при проведении поиска; время — количество секунд работы центрального процессора до окончания поиска.

Таблица 3.4. Результаты решения задач (№10) Изона и Фентона (х⁽⁰⁾ = [0,5, 0,5])

Метод	Метод
	деления интервала пополам	золотого сечения	Коггинса	кубической апроксимации
Коши	1.744 / 0,299 / 1026а)	1.744 / 0,219 / 688	1.744 / 0,181 / 312	1.744 / 0.091 / 171
Флетчера — Ривса	1.744 / 0.066 / 249	1.744 / 0.053 / 199	1.744 / 12.21 / 28141	1.744 / 0.025 / 92
Дэвидона — Флетчера — Пауэлла	1.744 / 0.056 / 232	1.744 / 0.051 / 184	1.744 / 0.09 / 208	1.744 / 0.079 / 262
Бройдена — Флетчера — Шэнно	1.744 / 0.055 / 226	1.744 / 0.051 / 176	1.744 / 0.087 / 195	1.744 / 0.043 / 133

^а) f (x*) / время / К.Ф.

Таблица 3.5. Результаты исследования функции Вуда (х⁽⁰⁾ = [–3, –1, –3, –1])

Метод	Метод
	деления интервала пополам	золотого сечения	Коггинса	кубической апроксимации
Коши	3.74E-9 / 13.466 / 39503а)	1.77E-8 / 10.70 / 29 / 692	2.95E-9 / 5.844 / 12.392	8.36E-6 / 7.89 / 20.007
Флетчера — Ривса	1.3E-10 / 0.401 / 1257	1.2E-8 / 0.311 / 942	2.9E-8 / 0.571 / 1468	2.0E-7 / 0.083 / 244
Дэвидона — Флетчера — Пауэлла	3.9E-9 / 0.810 / 2404	3.7E-9 / 0.684 / 1895	2.9E-9 / 0.403 / 747	9.5E-10 / 0.298 / 727
Бройдена — Флетчера — Шэнно	2.2E-9 / 0.759 / 2054	2,0E-9 / 0.652 / 1650	2.0E-8 / 0.444 / 723	2.3E-9 / 0.240 / 410

^а) f (x*) / время / К.Ф.

f(x) =

Рис. 3.17. Линии уровня функции Изона и Фентона.

Функция Вуда: (x = x= 1)

f (x) = 100(x–x)+ (1 –x)+ 90(x– x)+ (1–x)+ 10.1[(x– 1)+ (x– 1)]+ 19.8(x– 1)(x– 1).

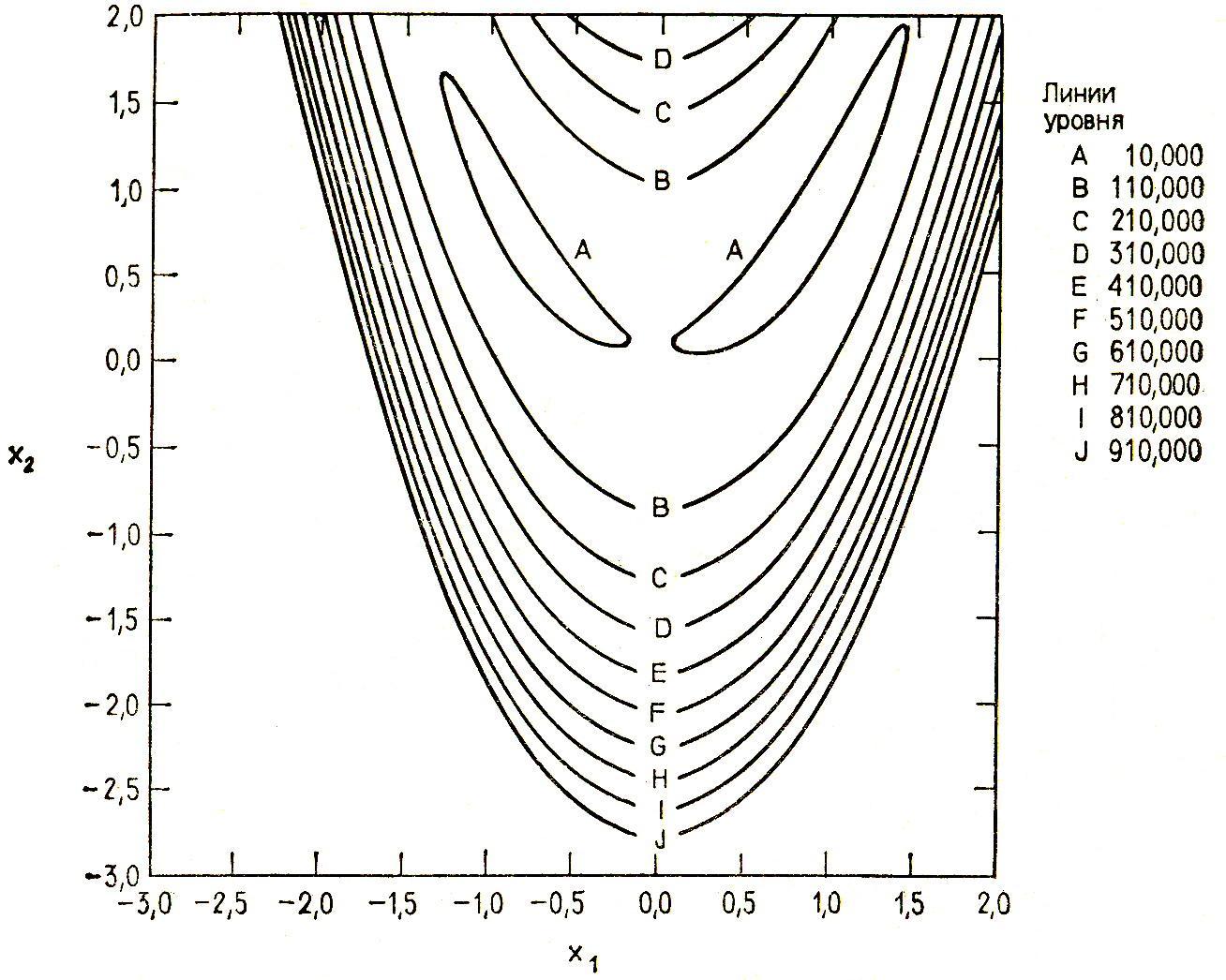
Рис. 3.18. Линии уровня функции Вуда.