Теорема 2.1

Необходимые условия того, что х* является точкой локального минимума (максимума) дважды дифференцируемой функции f на открытом интервале (а, b), выражаются следующими соотношениями:

Эти условия являются необходимыми, т. е. в случае, когда они не выполняются, точка х* не может быть точкой локального минимума (максимума). С другой сторо­ны, если эти условия выполня­ются, мы не имеем гарантии, что х* является точкой локаль­ного минимума (максимума). Рассмотрим, например, функцию f(x)=x³, график которой пред­ставлен на рис. 2.8. Эта функ­ция удовлетворяет необходимым условиям наличия как локаль­ного минимума, так и локаль­ного максимума в начале коор­динат, однако не имеет ни мак­симума, ни минимума при х*=0.

Определения

Стационарной точкой называется точка х*, в которой

Если стационарная точка не соответствует локальному оптиму­му (минимуму или максимуму), то она является точкой перегиба, или седловой точкой.

Для того чтобы провести различие между случаями, когда ста­ционарная точка соответствует локальному минимуму, локальному максимуму или является точкой перегиба, необходимо построить достаточные условия оптимальности.

Теорема 2.2

Пусть в точке х* первые (п—1) производные функции обращаются в нуль, а производная порядка п отлична от нуля.

(1) Если п — нечетное, то х*— точка перегиба.

2. Если п — четное, то х*— точка локального оптимума.

Кроме того,

(а) если эта производная положительная, то х*— точка локаль­ного минимума;

(б) если эта производная отрицательная, то х*— точка локаль­ного максимума.

Доказательство

Утверждение теоремы нетрудно доказать с помощью разложения в ряд Тейлора, представленного равенством (2.1). Поскольку поря­док первой отличной от нуля производной равен п, формулу (2.1) можно переписать в следующем виде:

Если п — нечетное число, то правая часть (2.6) может принимать как положительные, так и отрицательные значения в зависимости от того, является ли величина  положительной или отрицательной. Это означает, что в зависимости от знака  разность f(x*+) - f (x*) либо положительная, либо отрицательная. Следовательно, функция не достигает в точке х* своего минимального или максимального значения, т. е. х*— точка перегиба.

Далее рассмотрим случай, когда п — четное число. При этом ве­личина ⁿ всегда положительная, а знак правой части (2.6) опреде­ляется первым слагаемым, если  — достаточно малая величина. Таким образом, если величина (dⁿf /dxⁿ )_x=x* положительная, то f(x*+)- f (х*)>0 и точка х* соответствует локальному минимуму. Аналогичные рассуждения нетрудно провести также и для локаль­ного максимума.

Для того чтобы применить теорему 2.2 к функции f(x)=x³, гра­фик которой изображен на рис. 2.8, вычислим

Так как порядок первой отличной от нуля производной равен 3 (нечетное число), точка х=0 является точкой перегиба.

Замечание

Выше предполагалось, что рассматриваемая функция диффе­ренцируема или что ее первая производная существует и непрерыв­на. Однако если функция не является дифференцируемой во всех точках области определения, то даже необходимое условие наличия оптимума, позволяющее идентифицировать стационарные точки, может не выполняться в точке оптимума. Например, рассмотрим кусочно-линейную функцию

Эта функция непрерывна во всех точках действительной оси, но не­дифференцируема при х=2. Функция достигает максимума в точке х=2, которая не является стационарной в соответствии с данным выше определением.

Пример 2.1

Рассмотрим функцию

определенную на всей действительной оси. Первая производная этой функции равна

df /dx =30х^{5 +} 180х⁴+ 330х³— 180х² = 30х² (х—1) (х—2) (х—3).

Ясно, что первая производная обращается в нуль в точках х = 0, 1, 2, 3, и, следовательно, эти точки можно классифицировать как стационарные. Вторая производная функции равна

Вычислив значения второй производной в четырех точках х = 0, 1, 2, 3, получим

x	f(x)	d2f /dx2
0	36	0
1	27,5	60
2	44	-120
3	5,5	540

Отсюда следует вывод, что х=1, 3 — точки локальных минимумов, а х=2 — точка локального максимума. Чтобы идентифицировать точку х=0, вычислим третью производную

Так как эта производная отлична от нуля и имеет нечетный порядок, то точка х=0 является не точкой оптимума, а точкой перегиба.

Следующий вопрос, к рассмотрению которого мы переходим, связан с определением глобального максимума или минимума функ­ции одной переменной. Поскольку глобальный оптимум является локальным, можно вычислить все локальные оптимумы и выбрать из них наилучший. Алгоритм, основанный на этом простейшем подходе, приводится ниже.

Максимизировать f(x) при ограничении а ≤ x ≤ b,

где а и b — установленные границы изменения значений перемен­ной х.

Так как функция исследуется на заданном интервале, нетрудно заметить, что проверку наличия локального оптимума необходимо проводить не только в стационарных точках, но и в граничных точках интервала.

Шаг 1. Приравнять df/dx=0 и найти все стационарные точки.

Шаг 2. Выбрать все стационарные точки, которые располо­жены в интервале [а, b. Обозначим эти точки через x₁, х₂, . . . , х_N.

Проверку наличия локального оптимума следует проводить только на множестве указанных точек, дополненном точками а и b.

Шаг 3. Найти наибольшее значение f(x) из множества f(а), f(b), f(x₁), . . . , f(x_N). Это значение соответствует глобальному максимуму.

Примечание. При построении алгоритма мы не пытались клас­сифицировать стационарные точки как точки локального минимума, точки локального максимума или точки перегиба, поскольку для этого требуется вычисление производных высших порядков. Для определения глобального оптимума легче вычислить соответствую­щие значения функции и выбрать из них максимальное.

Пример 2.2

Максимизировать f(x)= - x³+Зх²+9х+10 на интервале -2≤ х ≤4. Имеем

Решая это уравнение, получаем две стационарные точки х=3 и x= -1, которые расположены внутри заданного интервала.

Для того чтобы найти глобальный максимум, вычислим значения f(x) в точках х = 3, - 1, - 2 и 4:

Таким образом, точка х =3 соответствует максимальному значению f на интервале [—2, 4].

Вместо перебора всех стационарных точек и соответствующих значений функции можно воспользоваться специальными процеду­рами, позволяющими найти глобальный оптимум с меньшими за­тратами времени при условии, что функция обладает определенными свойствами. В заключительной части разд. 2.1 было дано определе­ние унимодальной функции, для которой локальный оптимум яв­ляется глобальным. К сожалению, определение унимодальной функ­ции не позволяет непосредственно проверить, является ли функция унимодальной. Однако в теории оптимизации выделяется важный класс унимодальных функций, а именно класс выпуклых и вогнутых функций, которые допускают проверку такого рода. Основные свойства выпуклых и вогнутых функций приведены в приложении Б.

Пример 2.3

Исследуем свойства функции

При х≤1 имеем f"(х)≤0, и, следовательно, функция является вог­нутой в указанной области. Если же х 1 то f"(x)0, т. е. функ­ция является выпуклой в этой области.

Заметим, что функция имеет две стационарные точки х= -¹/₂ и x= ⁵/₂. Поскольку f"(-¹/₂)<0, функция обладает локальным мак­симумом при х= -¹/₂. В точке x= ⁵/₂ вторая производная f"(⁵/₂)>0, и, следовательно, функция достигает в этой точке локального ми­нимума. Если ограничить допустимую область неравенством х≤1, то f(x) имеет глобальный максимум при х= -¹/₂, так как f(x) — вогнутая функция (в данной области) и х= -¹/₂ — точка локаль­ного максимума. Аналогично если ограничить допустимую область неравенством х1, то f(x) достигает глобального минимума при х= ⁵/₂. Однако если переменная х изменяется на всей действительной оси от -∞ до +∞, то функция f(x) не имеет конечного глобального максимума или минимума.

Пример 2.4. Задача управления запасами

Многие фирмы создают запасы производимых товаров для удов­летворения будущего спроса. Среди причин, обусловливающих содержание запасов в определенном объеме, можно отметить нера­циональные потери времени и средств, связанные с их непрерывным пополнением. С другой стороны, пополнение запасов через продол­жительные промежутки времени приводит к образованию чрезмерно больших запасов, которое требует необоснованных капитальных затрат и значительно повышает стоимость хранения запасов. Опре­деление оптимального объема запасов представляет собой классиче­скую задачу оптимизации, для решения которой часто используется так называемая модель определения наиболее экономичного размера заказа.

В рамках этой модели спрос предполагается постоянным и рав­ным , единиц товара в год. Частое пополнение запасов нецелесооб­разно, так как стоимость выполнения одного заказа составляет К долл. независимо от его размера. Первоначальная стоимость еди­ницы товара равна с долл. Хранение излишних запасов также не­целесообразно, поскольку стоимость хранения единицы товара от­лична от нуля и составляет h долл. в год. Для того чтобы упростить задачу, предположим, что спрос удовлетворяется немедленно (т. е. задолженные заказы отсутствуют), а пополнение осуществляется сразу же, как только запасы иссякают.

Рис. 2.9 иллюстрирует изменение объема запасов с течением времени. В точке А объем запасов равен В; затем объем запасов начинает уменьшаться со скоростью  единиц товара в единицу вре­мени и достигает нулевого значения в точке С. В это время посту­пает новая партия товара, и объем запасов восстанавливается.

Треугольник ABC представляет один цикл управления запасами, который повторяется во времени. Задача заключается в том, чтобы определить оптимальный размер заказа В и продолжительность интервала времени между заказами С — А. Обозначим соответ­ствующие переменные через Q и Т.

Поскольку Т есть величина промежутка времени, в течение ко­торого при скорости расходования  истощается запас Q, имеем T=Q/. Таким образом, задача сводится к нахождению оптималь­ного значения Q. Заметим, что когда Q мало, переменная Т также принимает малое значение. При этом частота заказов велика, что обусловливает большие затраты на выполнение заказов и относи­тельно малые издержки хранения запасов. С другой стороны, нали­чие большого объема запасов (Q велико) приводит к увеличению затрат на хранение запасов и одновременно к снижению издержек, связанных с выполнением заказов на товары. Одна из основных задач управления запасами состоит в определении оптимального значе­ния Q, которому соответствует минимум суммы полных годовых затрат.

Получим аналитическое выражение для функции полных годо­вых затрат (затраты/цикл x количество циклов/год).

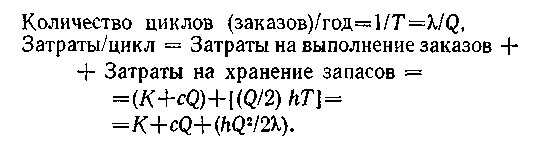
Примечание. Затраты на хранение запасов в течение цикла рав­ны затратам на хранение Q/2 единиц товара в течение интервала времени Т.

Таким образом, подлежащая минимизации функция полных затрат есть

Отсюда следует, что f(Q) — выпуклая функция и если существует положительное значение Q*, такое, что f(Q*)=0, то Q* минимизи­рует f(Q).

При этом Т*— интервал времени между заказами =т . Величина Q* известна в теории управления запасами как наиболее экономичный размер заказа.